
- •Введение Металингвистические формулы
- •Простейшие приемы программирования. Оператор присваивания.
- •Разветвления
- •Простейшие циклы
- •Целочисленная арифметика
- •Сочетание цикла и разветвления
- •Вычисления с заданной точностью
- •Использование перечислений. Многозначное ветвление
- •Вычисления с хранением последовательности значений. Одномерные массивы
- •Вложенные циклы.
- •Вложенные циклы в матричных задачах.
- •Дана действительная квадратная матрица . Получить две квадратные матрицы, , , для которых
- •Обработка последовательностей символов
- •Геометрия
- •Многочлены
- •Использование комбинированных типов Использование подпрограмм
- •Рекурсия Файлы
- •Сортировка массивов и файлов Системы счисления Связное представление данных в памяти
- •Двоичные деревья
- •Примерные варианты контрольных работ Контрольная работа №1
Простейшие циклы
Дано натуральное число n. Вычислить
 ;
; ;
;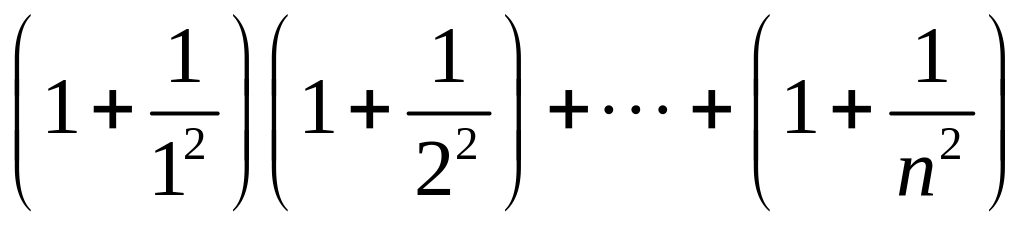 ;
; ;
; ;
; ;
; ;
; .
.
Дано натуральное число . Вычислить
![]() .
.
Даны действительное число , натуральное число . Вычислить:
 ;
; ;
; ;
; ;
; .
.
Вычислить
 .
.Дано действительное число . Вычислить
 .
.
Даны действительные числа , , натуральное число . Вычислить
 .
.Дано действительное число . Вычислить
 .
.
Дано действительное число . Найти:
среди чисел
 ,
,
 ,
,
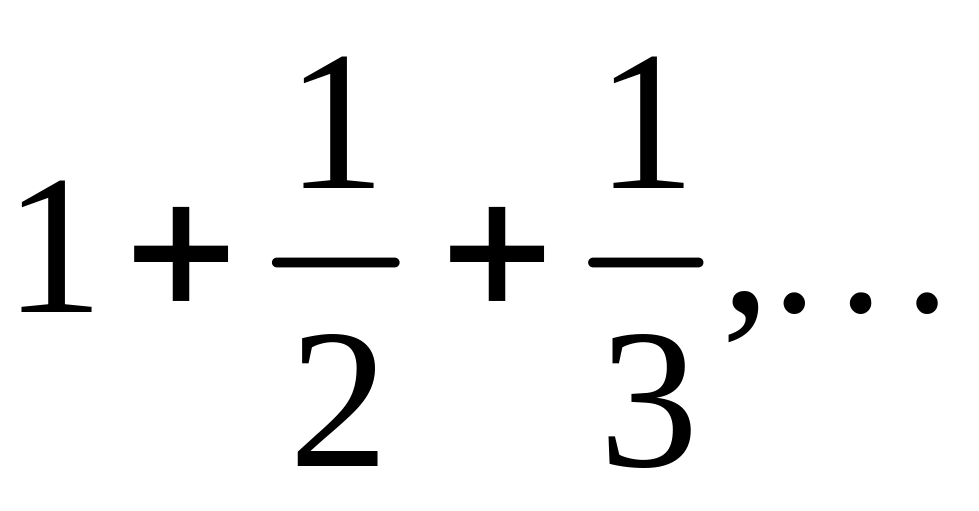 первое, большее
;
первое, большее
;такое наименьшее , что
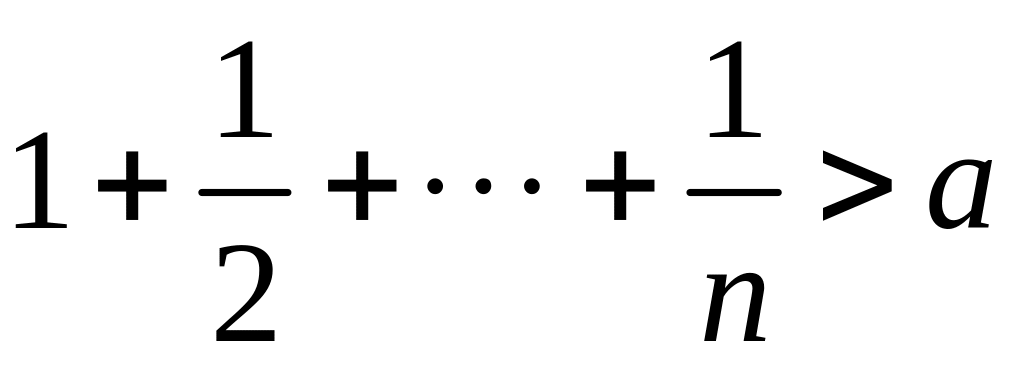 .
.
Найти — первый отрицательный член последовательности
 ,
,
 .
.Имеется целое
 .
Вычислить
—
-ый
член последовательности
.
Вычислить
—
-ый
член последовательности
 ,
где
,
где
 ,
,
 при
.
при
.Вычислить по схеме Горнера:
 ;
; .
.
Даны натуральное , действительное . Вычислить:
 ;
; ;
; .
.
Пусть
 ;
;  Дано
натуральное число
.
Получить
Дано
натуральное число
.
Получить
 .
.Пусть
 ;
;  ;
;  Дано
натуральное число
(
Дано
натуральное число
( ).
Получить
).
Получить
 .
.Пусть
 ;
;  ;
;  Даны
действительные
,
Даны
действительные
,
 ,
,
,
,
натуральное
(
,
,
,
,
натуральное
( ).
Получить
).
Получить
 .
.Пусть
 ;
;  ;
;

 Дано
натуральное число
(
Дано
натуральное число
( ).
Получить
.
).
Получить
.Пусть
 ;
;  Найти
произведение
Найти
произведение
 .
.Пусть
 ;
;  ;
;
![]() Дано
натуральное число
.
Найти
Дано
натуральное число
.
Найти
 .
.
Пусть
 ;
; 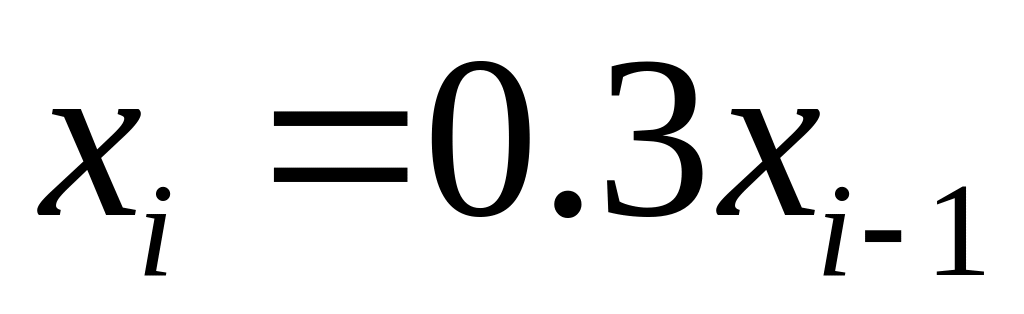 ;
;  Дано
натуральное число
.
Найти
Дано
натуральное число
.
Найти
 .
.Пусть ;
 ;
;  Дано
натуральное число
.
Найти
Дано
натуральное число
.
Найти
 .
.Пусть
 ;
; 
 ;
Даны
действительные
,
;
Даны
действительные
,
 ,
натуральное
.
Найти
,
натуральное
.
Найти
 .
.Пусть
 ;
;  ;
Найти
;
Найти
 .
.Даны положительные действительные числа , ,
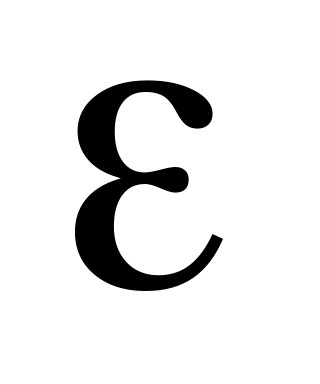 .
В последовательности
.
В последовательности
 ,
образованной по закону
,
образованной по закону
![]() ;
;
 ,
найти
первый член
,
найти
первый член
![]() .
для которого выполнено неравенство
.
для которого выполнено неравенство
![]() .
.
Пусть ;
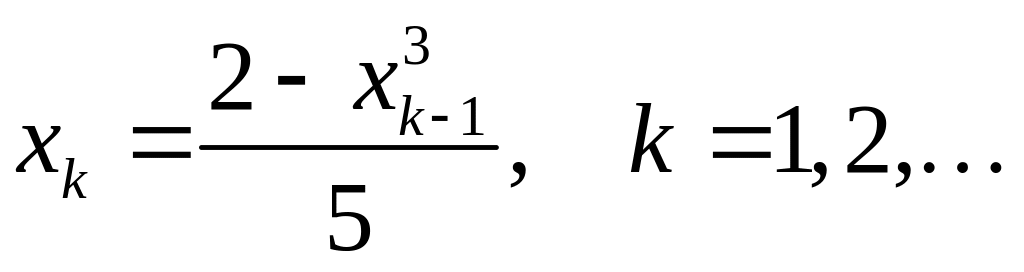 .
Найти
первый член
.
для которого выполнено неравенство
.
Найти
первый член
.
для которого выполнено неравенство
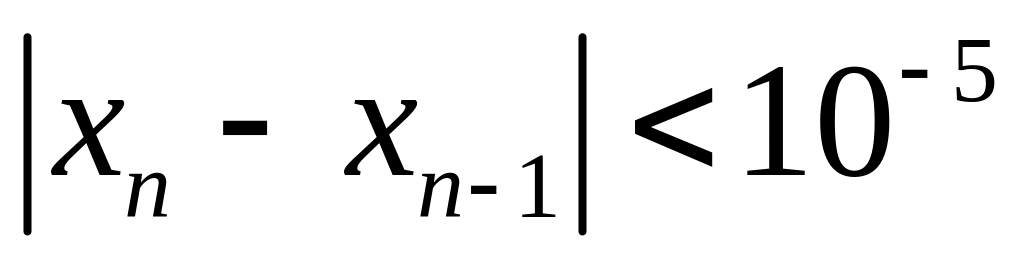 .
.Пусть
 ;
;  .
Дано
действительное
.
Дано
действительное
 .
Найти первый член
.
для которого выполнено неравенство
.
Найти первый член
.
для которого выполнено неравенство
 .
.Дано действительное число
 .
Последовательность
.
Последовательность
 образована по закону
образована по закону

 ,
Найти
первый член
.
для которого выполнено неравенство
,
Найти
первый член
.
для которого выполнено неравенство
![]() .
Вычислить для найденного значения
разность
.
Вычислить для найденного значения
разность
![]() .
.
Даны натуральное число , действительное число . Вычислить:
 ;
; .
.
Дано целое число
 .
Получить наибольшее целое
,
при котором
.
Получить наибольшее целое
,
при котором
 .
.Дано натуральное число . Получить наименьшее число вида
 ,
превосходящее
.
,
превосходящее
.Дано натуральное число . Вычислить
![]() .
.
Вычислить
 .
.
Дано действительное число
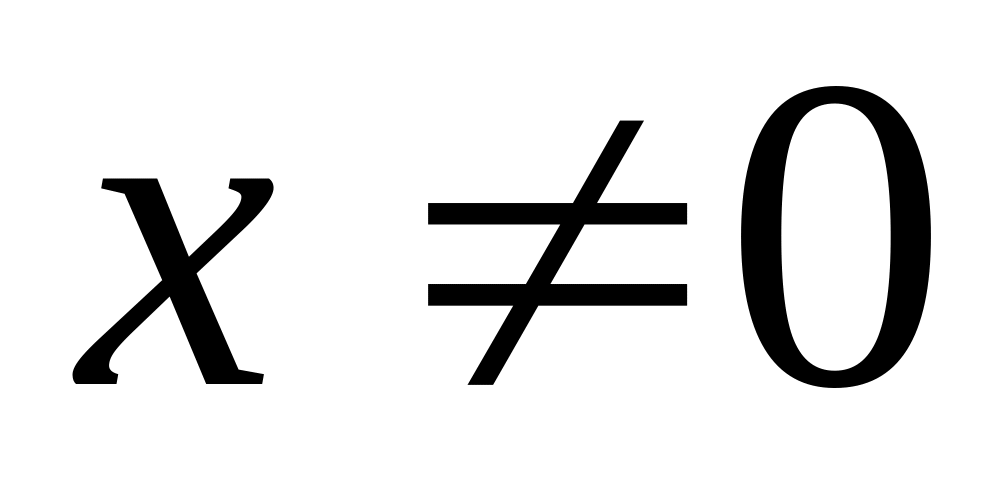 .
Вычислить
.
Вычислить
 .
.
Даны целые числа , (
 ).Вычислить
).Вычислить
 .
.
Пусть натуральное число и пусть
 означает
означает
 для нечетного
и
для нечетного
и
 для четного
.
Для заданного натурального
вычислить:
для четного
.
Для заданного натурального
вычислить:
;
 .
.
Вычислить:
 ;
;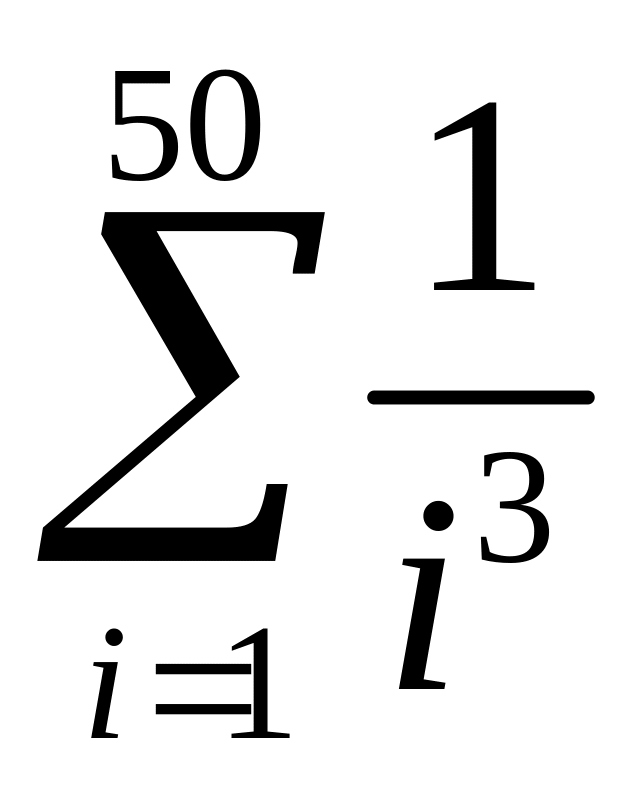 ;
; ;
; ;
; ;
; ;
; ;
; .
.
Дано натуральное число . Вычислить:
 ;
; ;
; ;
; ;
;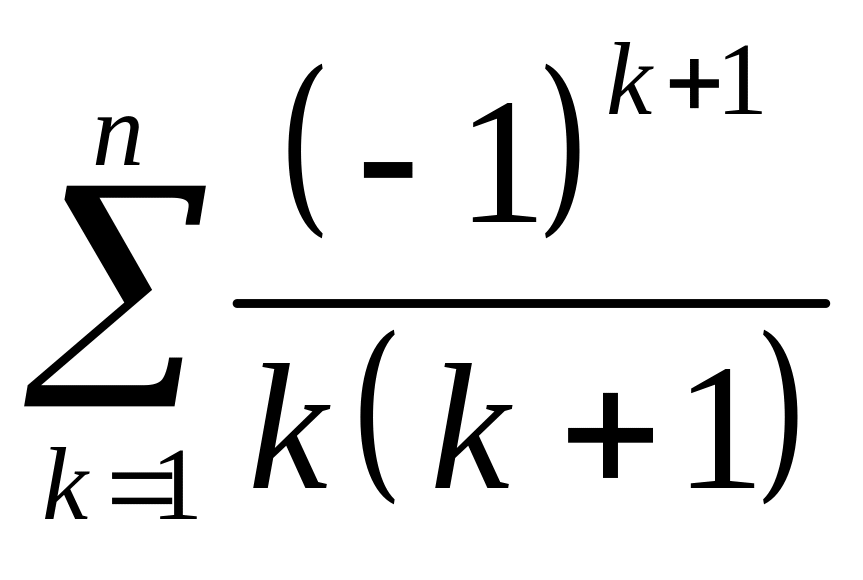 ;
; ;
; .
.
Дано натуральное число , действительное число . Вычислить:
 ;
; ;
; ;
;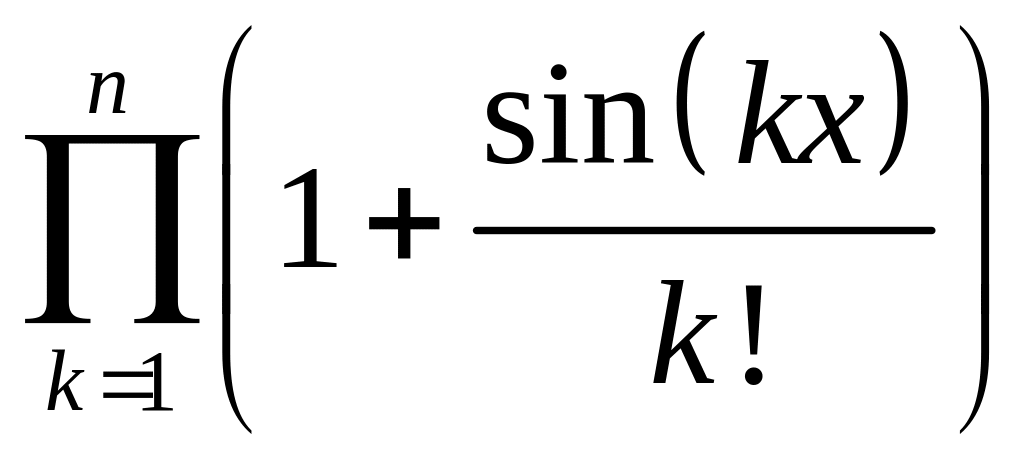 ;
; ;
; ;
;
Дано натуральное число . Вычислить произведение первых сомножителей:
 ;
; .
.
Вычислить
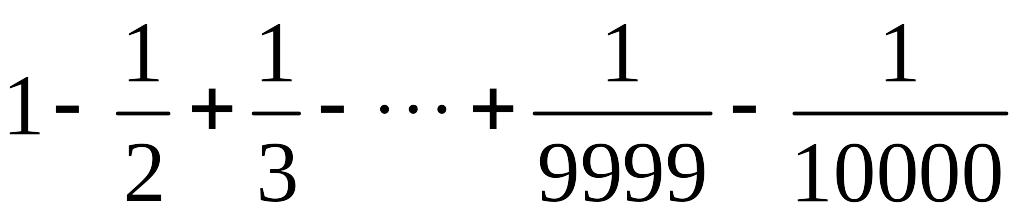 следующими четырьмя способами:
следующими четырьмя способами:последовательно слева направо;
последовательно слева направо вычисляются
 и
и
 ,
затем второе значение вычитается из
первого;
,
затем второе значение вычитается из
первого;последовательно cправа налево;
последовательно cправа налево вычисляются суммы, выписанные в b, затем вычитание. Почему при вычислениях на вычислительной машине каждым из этих способов получаются разные результаты?
Вычислить бесконечную сумму с заданной точностью ( ). Считать, что требуемая точность достигнута, если вычислена сумма первых слагаемых, и очередное слагаемое оказалось по модулю меньше, чем , это и все последующие слагаемые можно уже не учитывать:
 ;
; ;
; ;
; ;
; ;
;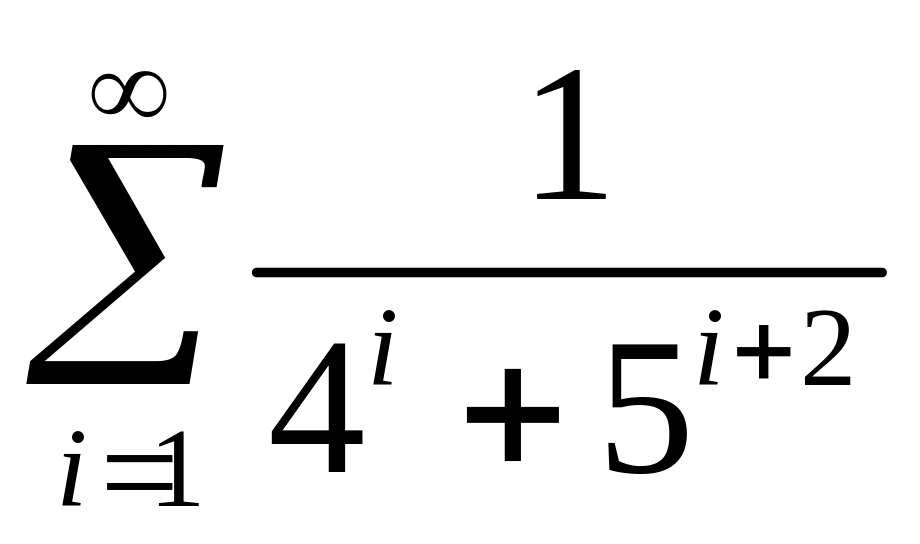 .
.
Вычислить сумму квадратов всех целых чисел, попадающих в интервал (
 )
) .
.Вычислить количество точек с целочисленными координатами, попадающими в круг радиуса
 (
( )
с центром в начале координат.
)
с центром в начале координат.Если среди чисел
 (
( )
есть хотя бы одно отрицательное число,
то логической переменной
присвоить значение
)
есть хотя бы одно отрицательное число,
то логической переменной
присвоить значение
 ,
а иначе значение
,
а иначе значение
 .
.
