Обработка последовательностей символов

Проверить, правильно ли в заданном тексте расставлены круглые скобки (т. е. находится ли справа от каждой открывающей скобки соответствующая ей закрывающая скобка, а слева от каждой закрывающей—соответствующая ей открывающая). Ответ—ДА или НЕТ.

Программа. Определить, является ли заданный текст правильной записью целого числа (возможно, со знаком).

Программа. Напечатать заданный текст, удалив из него лишние пробелы, т.е. из нескольких подряд идущих пробелов оставить только один.

Программа. Заданный текст распечатать по строкам, понимая под строкой либо очередные 60 литер, если среди них нет запятой, либо часть текста до запятой включительно.

В заданный непустой текст входят только цифры и буквы. Определить, удовлетворяет ли он следующему свойству:

а) текст является десятичной записью числа, кратного 9;

б) текст является записью четного числа в семеричной системе;

в) текст является десятичной записью числа, кратного 6;

г) текст является десятичной записью числа, кратного 4;

д) текст является шестнадцатеричной записью числа, кратного 5;

е) текст начинается с некоторой ненулевой цифры, за которой следуют только буквы, и их количество равно числовому значению этой цифры;

ж) текст начинается с k букв (1< k <9), за которыми

следует только одна литера—цифра с числовым значением k

з) текст совпадает с начальным отрезком ряда 0123456789 (например: 0, 01, 012);

и) текст совпадает с конечным отрезком ряда 0123456789 (например: 9, 89, 789);

к) текст совпадает с каким-то отрезком ряда 0123456789 (например: 2, 678);

л) текст состоит только из цифр, причем их числовые значения образуют арифметическую прогрессию (например: 2468, 741, 3);

м) текст содержит (помимо букв) только одну цифру, причем ее числовое значение равно длине текста;

н) сумма числовых значений цифр, входящих в текст, равна длине текста.

Геометрия

Даны действительные положительные числа , , , . Выяснить, можно ли построить четырехугольник с такими длинами сторон.
Даны действительные числа , , , ( ), которые определяют две точки ( , ) и ( , ). Найти на оси абсцисс такую точку, сумма расстояний от которой до точек и  наименьшая для всех точек этой оси.
Даны действительные числа , . Вычислить расстояние от точки плоскости с координатами ( , ) до границы квадрата с вершинами:
1. (-0,5 -0,5), (-0,5 0,5), (0,5 0,5), (0,5 -0,5);
2. (0, 0), (0, 1), (1, 1), (1, 0).
Даны натуральное число , целые числа , , , ,…, , . Известно, что точки ,…, с координатами ( , ), ( , ),…, ( , ) попарно различны. Пусть точка удалена от начала координат на расстояние ( ). Пусть .
1. Среди точек ,…, выбрать какую-нибудь одну для которой ; указать координаты выбранной точки и расстояние от этой точки до начала координат.
2. Среди точек ( ), для которых , выбрать те, которые обладают наименьшей абсциссой. Если таких точек больше одной, то выбрать из них точку, которая имеет наибольшую ординату. Указать номер выбранной точки.
В множестве точек на плоскости найти пару точек с максимальным расстоянием между ними.
Расстояние между двумя множествами точек  это расстояние между наиболее близко расположенными точками этих множеств. Найти расстояние между двумя заданными множествами точек на плоскости.
Порядок на точках плоскости определим следующим образом: ( , ) ( , ), если либо , либо 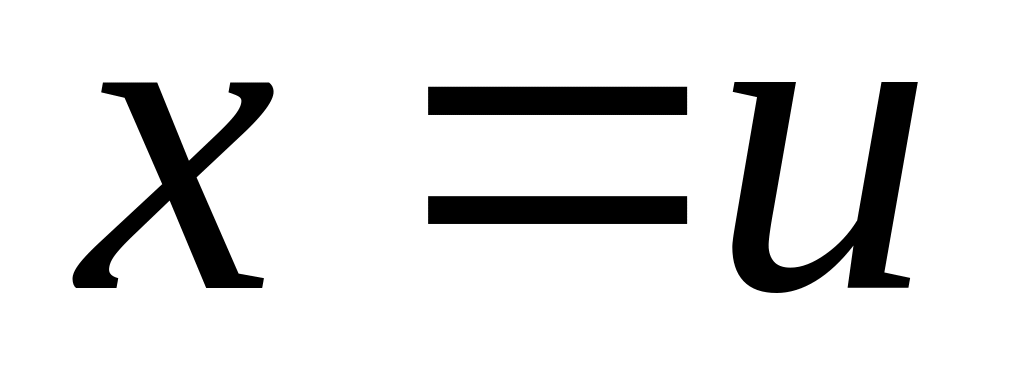и . Перечислить точки заданного множества точек на плоскости в соответствии с этим порядком.
Заданы два множества точек на плоскости. Построить пересечение и разность этих множеств.
Множество точек на плоскости назовем регулярным, если вместе с каждой парой различных точек оно содержит также еще одну  третью  вершину правильного треугольника с вершинами в этих точках. Определить, регулярно ли заданное множество точек.
Даны действительные числа ,…, . Эти числа определяют 25 интервалов числовой оси: ( , ), ( , ),…, ( , ).
1. Имеют ли все данные интервалы общие точки? Если да, то указать какую-нибудь из этих точек.
2. Является ли интервалом объединение данных интервалов? Если да, то указать концы этого интервала.
3. Указать число ( ) такое, что объединение данных интервалов можно представить в виде непересекающихся интервалов.
4. Имеются ли точки числовой оси, принадлежащие по крайней мере трем каким-нибудь из данных интервалов? Если да, то указать какую-нибудь из этих точек.
Даны действительные числа ,…, , ,…, , ,…, . Выяснить, есть ли на плоскости точка, принадлежащая всем кругам ,…, , где 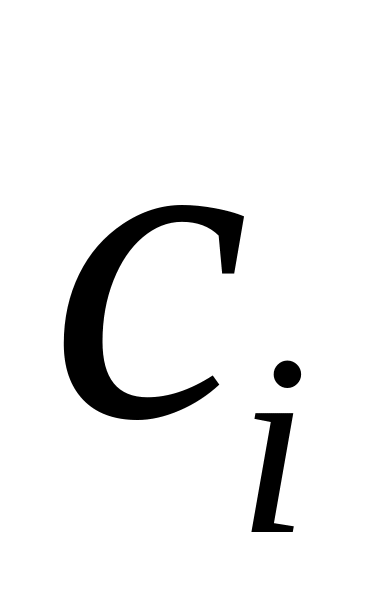имеет центр с координатами , и радиус ( ).
Даны действительные числа , , , ,…, , , которые рассматриваются как координаты ( , ), ( , ),…, ( , ) точек на плоскости. Выяснить, верно ли, что для каждой из этих пятнадцати точек найдется другая, такая, что все оставшиеся тринадцать точек лежат по одну сторону от прямой, проходящей через эти две точки.
Даны целые числа , , , ,…, , . Выяснить, найдутся ли среди точек с координатами ( , ), ( , ),…, ( , ) четыре таких, которые являются вершинами квадрата.
Даны целые числа , , , , , . Известно, что точки с координатами ( , ), ( , ), ( , ) являются тремя вершинами некоторого прямоугольника. Найти координаты четвертой вершины.
Прямая на плоскости может быть задана уравнением , где и одновременно не равны нулю. Будем рассматривать прямые только с целыми коэффициентами , , . Пусть даны коэффициенты нескольких прямых , , , , , ,…, , , .
1. Определить, имеются ли среди этих прямых совпадающие или параллельные.
2. Определить, имеются ли три прямые, пересекающиеся в одной точке.
3. Определить, находятся ли данные прямые в общем положении (Прямые находятся в общем положении, если все они различны, никакие две из них не параллельны, никакие три не пересекаются в одной точке).
Окружность на плоскости может быть задана координатами , ее центра и радиусом . Пусть даны соответствующие характеристики нескольких окружностей , , , , , ,…, , , .
1. Определить, имеются ли среди этих окружностей три попарно пересекающиеся.
2. Найти среди этих окружностей все уединенные окружности, т. е. такие, которые не имеют общих точек ни с одной из остальных окружностей, не лежат целиком внутри и не заключают внутри себя какой-либо из остальных окружностей.
Из заданного множества точек на плоскости выбрать две различные точки так, чтобы количества точек, лежащих по разные стороны прямой, проходящей через эти две точки, различались наименьшим образом.
Медианой множества, состоящего из четного числа точек плоскости, никакие три из которых не лежат на одной прямой, называется прямая, соединяющая две точки множества, с обеих сторон от которой лежит равное число точек. Даны действительные числа , , , ,…, , (  нечетное число). Найти число медиан множества точек с координатами ( , ), ( , ),…, ( , ) в предположении, что никакие три точки этого множества не лежат на одной прямой.
Д аны действительные числа , , , , , ,…, , , . Эта последовательность определяет на плоскости квадратов со сторонами, параллельными осям: ,  координаты центра квадрата,  длина его стороны ( ). Определить площадь фигуры, образованной всеми квадратами. Здесь может оказаться полезным предварительное решение следующей задачи. Стороны двух прямоугольников параллельны координатным осям. Каждый из прямоугольников задан четырьмя действительными числами  двумя абсциссами и двумя ординатами. Представить ту часть первого прямоугольника, которая не покрывается вторым прямоугольником, в виде объединения нескольких прямоугольников, не накладывающихся друг на друга.