
Пример 4.
Вычислить определенный интеграл из примера 1 методом Монте-Карло.
Введем исходные данные: отрезок интегрирования (А4:B4); количество отрезков разбиения (C4); формулу расчета шага интегрирования h (D4) (см. рис. 11).
Введем в ячейку B6 формулу =СЛЧИС()*(4–1)+1 (происходит генерация случайных чисел в диапазоне от 1 до 4) и заполним блок В6:В16.
Введем подынтегральную функцию
в ячейку С6 и заполним блок С6:С16.
Введем в ячейку C17 формулу =СУММ(C6:C16), а в ячейку C18 формулу =C17*D4.
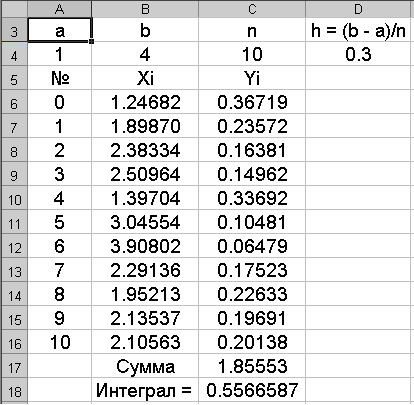
Рис. 11. Численное интегрирование по методу Монте-Карло
Задание
Составить сравнительную таблицу результатов численного решения определенного интеграла, полученных рассмотренными методами (см. табл. 1). Найти абсолютную и относительную погрешности вычислений, приняв в качестве истинного значения интеграла результат, полученный с помощью формулы Симпсона при n = 20.
Таблица 1
Численное интегрирование. Оценка погрешности
|
I10 |
(I) |
(I) |
I20 |
(I) |
(I) |
1-я ф-ла прямоуг. |
0,60419 |
0,05275 |
8,731% |
0,57761 |
0,02617 |
4,531% |
2-я ф-ла прямоуг. |
0,50028 |
0,05116 |
10,226% |
0,52566 |
0,02578 |
4,904% |
усл. ф-ла прямоуг. |
0,55104 |
0,00040 |
0,073% |
0,55134 |
0,00010 |
0,018% |
ф-ла трапеций |
0,55224 |
0,00080 |
0,145% |
0,55164 |
0,00020 |
0,036% |
ф-ла Симпсона |
0,55143 |
0,00001 |
0,002% |
0,55144 |
– |
– |
Обозначим приближенное значение интеграла буквой I, тогда

Указанная таблица составляется средствами Excel. Для этого значения интегралов, полученные рассмотренными методами при n = 10 и n = 20, переписываются вручную. Значения погрешностей вычисляются по вышеприведенным формулам.
ВАРИАНТЫ ЗАДАНИЙ
Вычислить интеграл по формулам прямоугольников (все разновидности), трапеций, Симпсона и методом Монте-Карло (n = 10). Обеспечить точность решения = 0,001. Полученные результаты сравнить с точными значениями интегралов, приведенными в ответах.
1. 2. 3.



4. 5. 6.
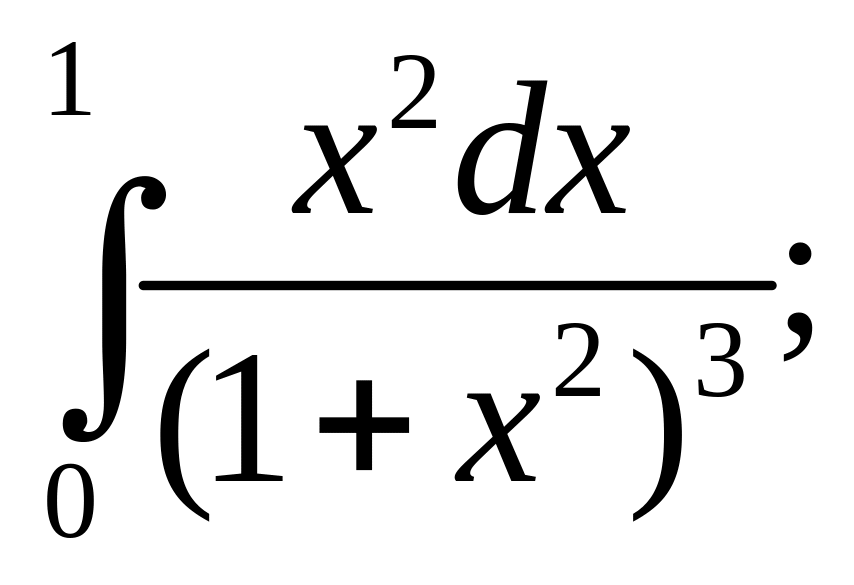


7. 8. 9.



10. 11. 12.



Ответы:
1. /2; 2. /6; 3. 32/3; 4. /32; 5. 2,5; 6. –1; 7. –2/9;
8.
![]() 9.
0,25
– 0,5ln 2; 10. (2e
sin 3 – 3e
cos 3 + 3)/13;
9.
0,25
– 0,5ln 2; 10. (2e
sin 3 – 3e
cos 3 + 3)/13;
11. 1; 12. arctg 4 – arctg 3.
