6. Пояснити відмінність між поняттями істотності та щільності зв’язку.

Встановлення факту істотності (тобто існування) або неістотності (тобто неіснування) цієї залежності.  Вимірювання щільності (тобто тісноти) зв’язку, який існує.

7. Для методу кореляційно-регресійного аналізу: а) назвати два основні етапи побудови рівняння регресії; б) назвати основні фактори, що визначають вибір виду рівняння регресії; в) навести назву та пояснити суть методу знаходження параметрів рівняння регресії; г) записати основні види рівнянь регресії та пояснити економічний або фізичний зміст їх параметрів; д) дати означення кореляційного поля; е) записати формули для обчислення регресійної та факторної дисперсій і пояснити зміст позначень; ж) назвати числову міру істотності та щільності зв’язку, записати формулу для її обчислення і пояснити зміст позначень; з) сформулювати правила, за якими визначається істотність та оцінюється щільність зв’язку, виявляється його напрям та характер.

У статистичній практиці найбільш поширеними видами рівнянь регресії є такі, параметри яких мають певний фізичний зміст, зокрема:

1. Лінійна залежність а+bх. Параметр а має зміст середнього значення ознаки Y при х=0; якщо ознака Х за своїм фізичним змістом не може приймати нульового значення, то а не має фізичного змісту. Параметр має зміст середньої швидкості зміни Y при зміні Х і показує, на скільки одиниць зміниться в середньому значення Y, якщо значення Х зміниться на одиницю.

2. Квадратична залежність р+qx+rx². Параметр р має той же зміст, що і параметр a для лінійного рівняння регресії. Параметр q має зміст середньої початкової швидкості зміни Y при зміні Х. Параметр 2r має зміст середнього прискорення зміни Y при зміні Х і показує, на скільки одиниць в середньому зміниться середня швидкість зміни Y, якщо значення Х зміниться на одиницю.

Вибір виду рівняння регресії в кожному конкретному дослідженні залежить, в основному, від двох факторів: 1) виду кореляційного поля, яке в даному випадку являє собою сукупність точок з координатами (х_і; у_і) ( ), побудованих в прямокутній системі координат хоу; 2) ретельного вивчення суті явища, що досліджується, з урахуванням результатів попередніх аналогічних досліджень, якщо останні проводились.

Параметри рівняння регресії f(x) зазвичай знаходяться за методом найменших квадратів, який забезпечує такий вибір їх числових значень, щоб сума квадратів відхилень емпіричних значень у_і ознаки Y від відповідних теоретичних (або вирівняних) значень f(x_і) була найменшою:

.

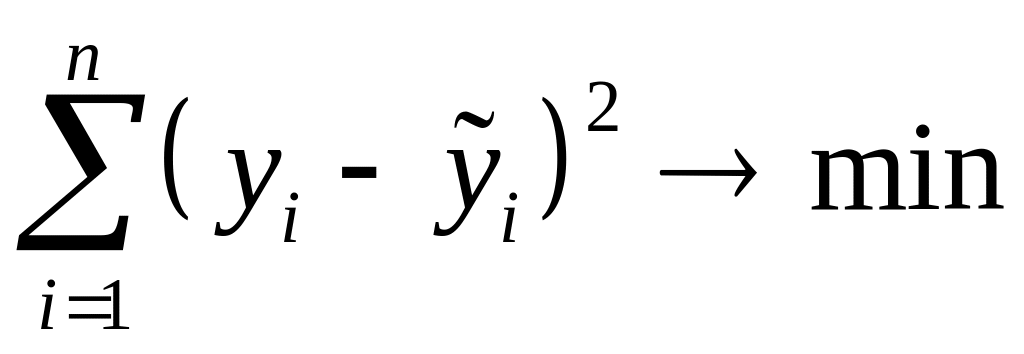Величина

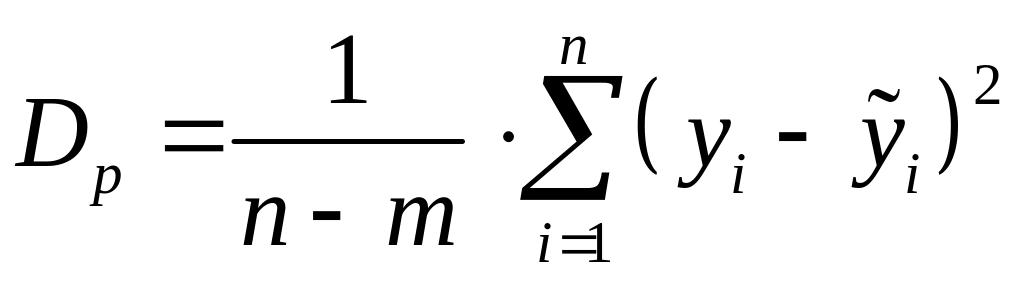, (3.11)

де п – число пар (х_і; у_і), m – число параметрів рівняння регресії, які знаходяться за даними вибірки, називається регресійною дисперсією і може слугувати критерієм вибору виду рівняння регресії.

Числовою мірою щільності та істотності зв’язку в КРА є коефіцієнт детермінації

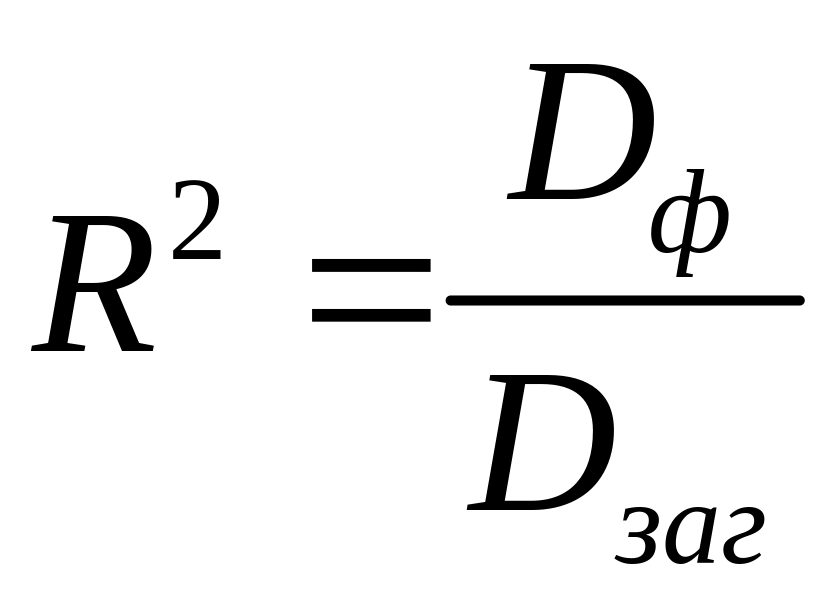, (3.15)

де – загальна дисперсія результативної ознаки Y, яка обчислюється за формулою (3.3), D_ф – факторна дисперсія ознаки Y, яка обчислюється за формулою:

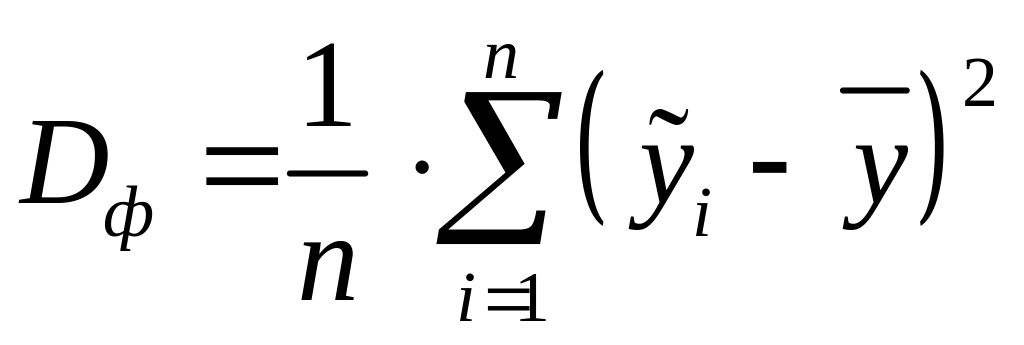. (3.16)

8. Для методу збігу знаків: а) записати формулу для обчислення коефіцієнта кореляції знаків та пояснити зміст позначень; б) сформулювати правила, за якими виявляється напрям та оцінюється істотність і щільність зв’язку.

Числовою мірою щільності та істотності зв’язку в даному методі є коефіцієнт кореляції знаків Фехнера ( або коефіцієнт збігу знаків), який обчислюється за формулами (3.17) або (3.18) :

; (3.17)

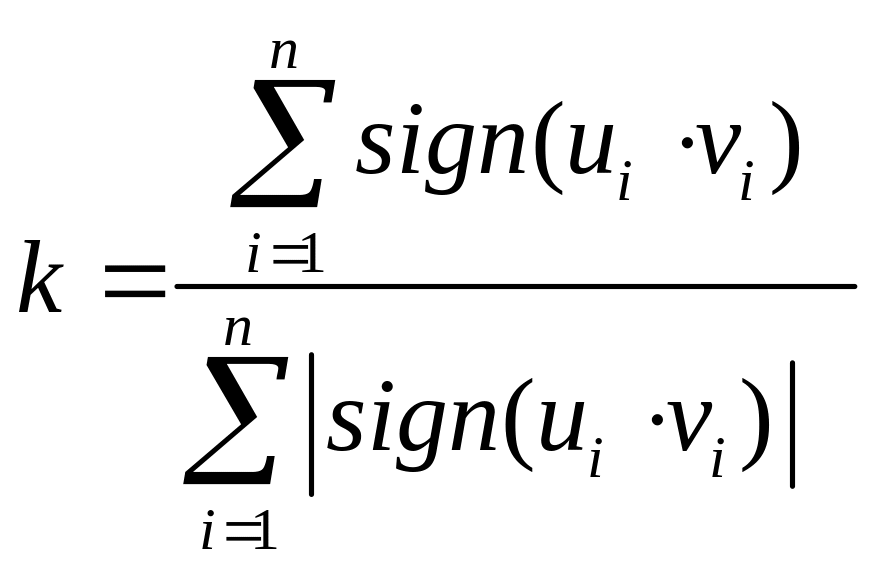, (3.18)

де n – обсяг вибірки, тобто, загальне число пар ( ); А(В) – число пар з однаковими (різними) знаками значень та ;

; (3.19)

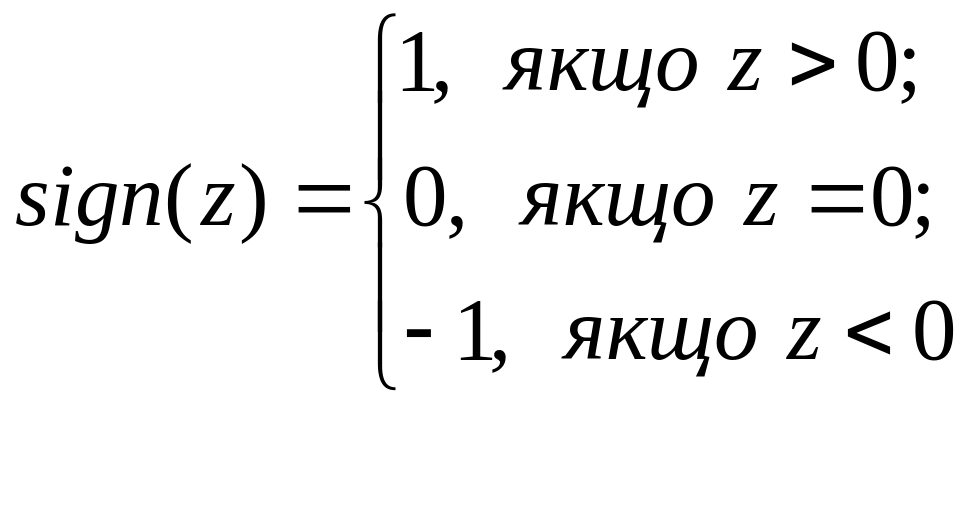(3.20)

- знакова функція.

Напрям можливої залежності визначається знаком k: якщо ,то зв'язок прямий (зворотний), тобто, із збільшенням значень однієї з ознак значення іншої збільшуються (зменшуються).

Перевірка істотності (тобто, існування) зв’язку здійснюється за правилом: якщо , то зв'язок вважаємо неістотним (істотним). При цьому - спостережене, тобто, обчислене за даними вибірки за формулою (3.17) значення коефіцієнту збігу знаків; - критичне значення коефіцієнту збігу знаків, яке знаходиться за таблицею додатку 4 в залежності від обсягу вибірки і рівня значущості .

Вимірювання щільності зв’язку можна виконувати за правилом трисекції (див. п.п.2.3, 2.6). При цьому результати перевірки істотності і вимірювання щільності зв’язку слід вважати вірними з надійністю .

9. Для методу кореляції рангів Спірмена: а) дати визначення рангу варіанти; б) назвати числову міру істотності та щільності зв’язку, записати формулу для її обчислення та пояснити зміст позначень; б) сформулювати правила, за якими виявляється істотність та оцінюється щільність зв’язку і визначається його напрям.

Рангом u_i(v_i) кожного значення х_і(у_і) є його порядковий номер, якщо всі х_і(у_і) розташувати у неспадному порядку. Для перевірки істотності (тобто існування) зв’язку необхідно за формулою (3.21) обчислити спостережене значення величини і порівняти його модуль з критичним значенням , яке залежить від обсягу сукупності п та рівня значущості α і знаходиться за формулою:

,

де − рівень значущості; − число степенів вільності; − обсяг вибірки; − критична точка розподілу Стьюдента для двосторонньої критичної області (див. додаток 3).

Якщо , то зв’язок вважається істотним з імовірністю γ=( ) і навпаки. Рівень значущості зазвичай вибирається рівним 0,05 або 0,10 і являє собою імовірність ризику визнати зв’язок істотним, коли він насправді не існує.

Якщо зв’язок буде визнано істотним, то його щільність можна оцінювати за правилом трисекції:

• для 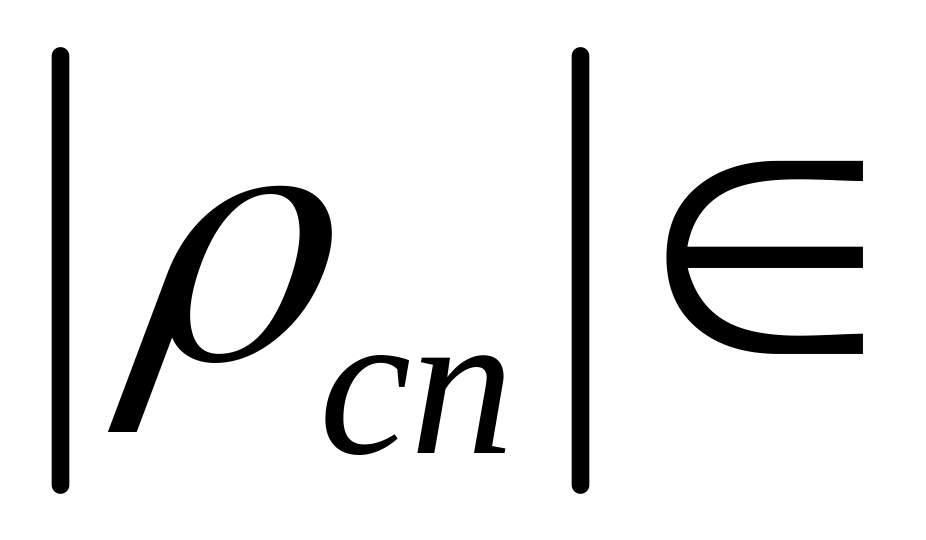(0,3 + 0,7; 1] зв’язок вважаємо щільним;

• для (0,7 + 0,3; 0,3 + 0,7] – помірним;

• для ( ; 0,7 + 0,3] – слабким.

Знак визначає напрям залежності: якщо , то зв’язок прямий і навпаки.