Матрица продолжительности работ
Частные фронты |
Частные потоки, расч. дни |
|||
А |
Б |
В |
Г |
|
1 |
10 |
12 |
9 |
6 |
2 |
12 |
12 |
22 |
6 |
3 |
18 |
12 |
39 |
6 |
4 |
26 |
12 |
51 |
6 |
5 |
22 |
12 |
39 |
6 |
6 |
8 |
12 |
21 |
6 |
сумма |
96 |
72 |
181 |
36 |
Трасч. |
40 |
15 |
151 |
|
Таблица №6.
Расчет периодов развертывания
Потоки |
Тразв. |
Трасч. |
|||||
1 |
2 |
3 |
4 |
5 |
6 |
||
Б/А |
10 |
10 |
16 |
30 |
40 |
36 |
40 |
В/Б |
12 |
15 |
5 |
-22 |
-61 |
-89 |
15 |
Г/В |
9 |
25 |
58 |
103 |
137 |
151 |
151 |
Общая продолжительность комплекса поточных работ рассчитывается по формуле:
Календарный график потока показан на циклограмме (рис. 2).
Рис. 2. Циклограмма потока с непрерывным использованием ресурсов.
Оптимизация потока по времени
При неизменных ресурсах механовооружения и неизменной продолжительности частных потоков на частных фронтах оптимизация потока по общей длительности поточных работ может быть произведена за счет рациональной очередности освоения частных фронтов, позволяющей добиться сокращения периодов развертывания.
Математическая модель поставленной задачи состоит из целевой функции и ограничений.
Целевая функция записывается в виде
При решении задачи ставятся два ограничения:
1. Длительность частных потоков на всех частных фронтах остается неизменной по сравнению с исходным вариантом.
2. Сохраняется условие непрерывности использования ресурсов и, следовательно, величина растяжения ресурсных связей для всех потоков равна нулю.
Последовательность намывных работ не нарушается от изменения очередности освоения частных фронтов. Выбор рациональной очередности ведения работ производится с помощью алгоритма В.А. Афанасьева.
Исходная матрица, состоящая из 4 частных потоков, разбивается на 3 парные подматрицы.
А Б В Г
А Б Б В В Г
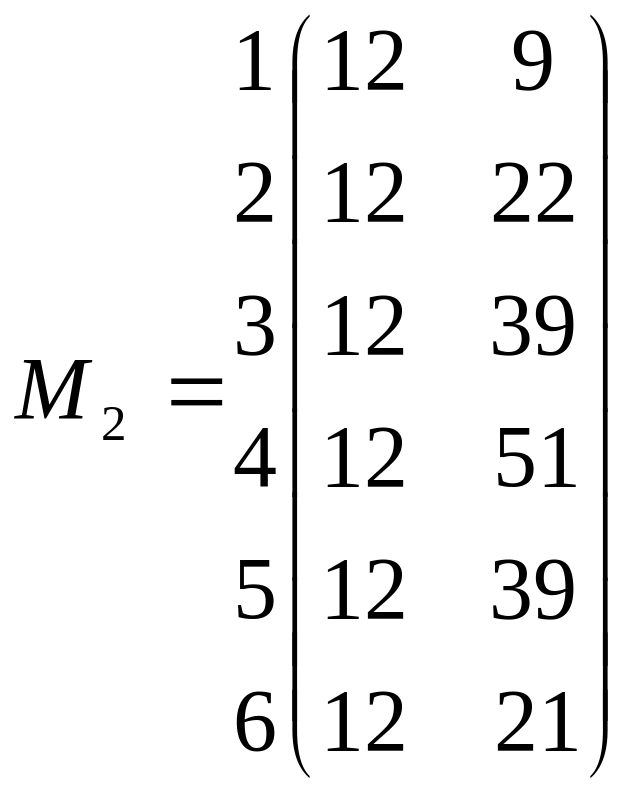
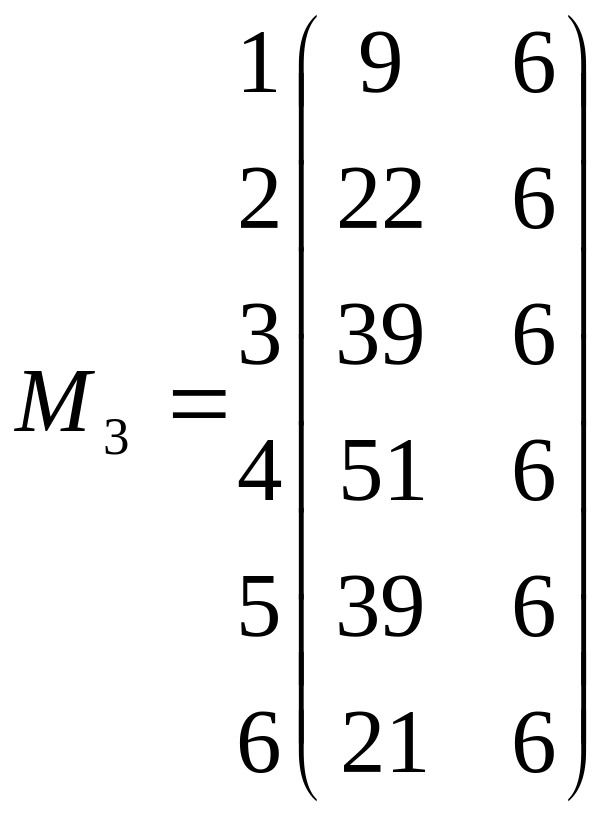
Для оптимизации по подматрице M1 определяем по правилу Джонсона оптимальную очередность освоения частных фронтов.
А Б
В соответствии с методом В.А. Афанасьева принимаем подматрицу М1опт за генеральную, определяющую очередность освоения частных фронтов, и вычисляем по ней периоды развертывания и общую продолжительность работ
А Б В Г
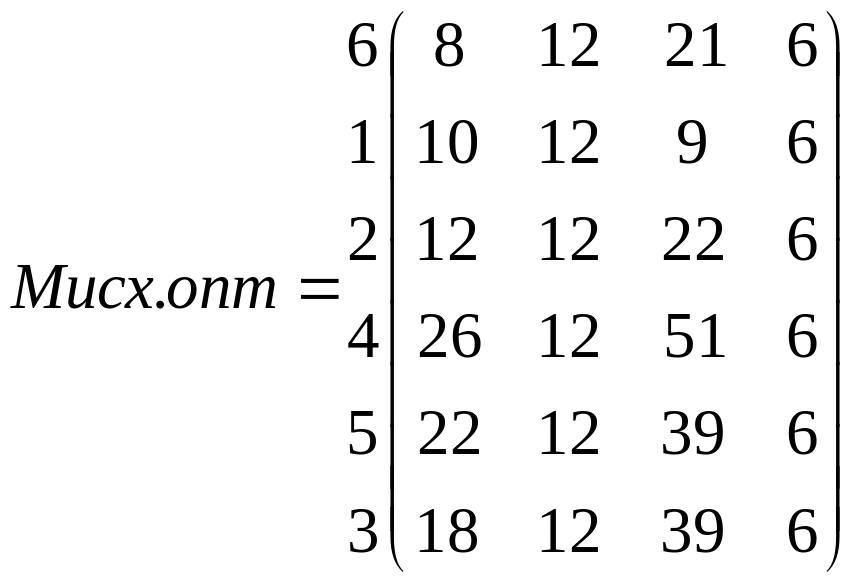
Расчет периодов развертывания частных потоков приведен в табл. 7.
Таблица №7.