2.4. Визначення регресійної лінійної моделі залежності виходу рибопродукції від щільності посадки риби.
Таблиця 4
№ досліду |
Щільність посадки однорічок коропа, екз/га
|
Рибопродуктивнысть, кг/га |
Розрахункові величини |
|
Xy, кг/га |
X2, тис. екз/га |
|||
1 |
700 |
364 |
254800 |
490000 |
2 |
900 |
441 |
396900 |
810000 |
3 |
1100 |
506 |
556600 |
1210000 |
4 |
1300 |
559 |
726700 |
1690000 |
5 |
1500 |
600 |
900000 |
2250000 |
6 |
1700 |
629 |
1069300 |
2890000 |
7 |
1900 |
646 |
1227400 |
3610000 |
8 |
2100 |
651 |
1367100 |
4410000 |
9 |
2300 |
644 |
1481200 |
5290000 |
10 |
2500 |
625 |
1562500 |
6250000 |
∑ |
16000 |
5665 |
9542500 |
28900000 |
|
1600 |
566,5 |
954250 |
2890000 |
Регресійну лінійну модель вираховуємо за системою двох рівнянь:
Підставляємо дані з таблиці в систему рівнянь:
5665 = b × 16000 + а × 10
9542500 = b × 28900000 + а × 16000
Поділивши перше рівняння на 10, а друге на 16000, отримаємо:
566,5 = b × 1600 + а
596,406 = b × 1806,25 + а
Далі віднімаємо одне рівняння від іншого:
-29,906 = b × ( - 206,25) + а
b = -0,145
Підставляємо в перше рівняння і отримуємо:
5665 =(-0,145) × 16000 + а × 10, звідси
а = (-0,145 × 16000) –5665/ 10 = -1753,5
Перевіряємо правильність побудови регресійної прямої:
= b × + а
5665 =(-0,145) × 16000 + (-1753,5) × 10
Таким чином шукане рівняння регресійного лінійного звязку має вигляд:
y = (-0,145) – (- 1753,5) × x
2.5. Графічна модель залежності виходу рибопродукції від щільності посадки.
Графічна модель залежності кінцевої маси від щільності посадки при вирощуванні коропа у полікультурі з рослиноїдними видами риб:
y = кінцева маса дволіток;
x = щільність посадки риби;
Коефіцієнт детермінації розраховується за формулою:
ryx
=
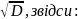D = ( ryx
)2
Сила зв’язку між показниками, існує тісний зв'язок, тому що коефіцієнт детермінації наближений до 1.
2.6. Графічна модель залежності кінцевої маси від щільності посадки.
Для визначення прогнозованих значень кінцевої маси риб використовуємо рівняння регресійного лінійного зв’язку:
y = (-0,145) – (- 1753,5) × x
Для визначення прогнозованих значень виходу рибопродукції використовуємо рівняння регресійного лінійного зв’язку:
у = 1,865 + (- 2599).
