Мищенко А. М. Лекции по электротехнике
.pdf
втором случае. Отметим, что в этих случаях изменение запасенной энергии магнитного и электрического поля в первый момент коммутации происходит скачком и лишь спустя некоторый момент времени плавно меняется. В электротехнике этот момент времени опускается.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называют независимыми начальными условиями. Они определяются на основе законов коммутации для элементов цепи. Математически они записываются так:
|
i |
(−t |
|
) = i |
|
(+t |
|
) = i |
|
(t |
|
) |
, |
(5.1.1) |
|
L |
|
k |
|
L |
|
k |
|
L |
|
k |
|
||
uC (−tk ) = uC (+tk ) = uC (tk ) |
|
|
||||||||||||
где tk – время момента коммутации, iL(-tk), uC(-tk) – ток в индуктивности и напряжение на емкости до момента коммутации, iL(+tk), uC(+tk) – соответственно в первый момент переходного процесса. Обычно, за время отсчета берут момент коммутации, т. е. полагают tk = 0. Из (5.1.1) следует два важных частных случая:
•при iL(−0) =0 и uC (−0) = 0 – индуктивность в момент коммутации равносильна разрыву, а емкость – короткому замыканию;
•при iL(−0) =i0 и uC (−0) = u0 – индуктивность в момент коммутации
равносильна источнику тока – i0, а емкость – источнику напряжения с ЭДС, равной u0.
В случаях, когда в цепи возможно изменение запасенной энергии магнитного и электрического поля скачком, независимые начальные условия выводят из сохранения суммарного заряд на емкостях в контуре и потока магнитного поля в контурах до и после коммутации.
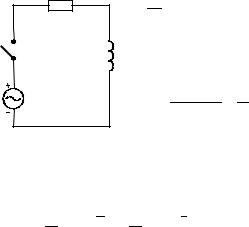
Пример 5.1.1. Рассмотрим в качестве примера две цепи: одна с контуром имеющем две индуктивности (см. рис. 5.1.1); другая с контуром из двух емкостей (см. рис. 5.1.2).
Рис. 5.1.1 |
Рис. 5.1.2 |
В первой цепи при замыкании ключа сохранение токов в индуктивностях после коммутации не вызывает нарушение закона токов Кирхгофа. Поэтому независимые начальные условия определяются
первым равенством в выражении (5.1.1), т. е. iL1 (−0) = iL1 (+0) ,
81
iL2 (−0) = iL2 (+0) , где за время отсчета взят момент коммутации. При
размыкании ключа сохранение токов в индуктивностях после коммутации вызове нарушение закона токов Кирхгофа. Это приведет к резкому увеличению напряжений на индуктивностях и как следствие пробой в ключе. Математически в выражении записанном по закону напряжений Кирхгофа для контура с индуктивностями основными слагаемыми будут
напряжения на индуктивностях L |
diL |
+ L |
diL |
0 . Эта ситуация |
|
1 |
2 |
||||
dt |
dt |
||||
1 |
2 |
|
сохранится в течении некоторого малого момента времени. За этот промежуток времени магнитные поля перераспределяются между катушками. В электротехнике этими временами пренебрегают. Поэтому,
интегрируя L1 didtL1 + L2 didtL2 0 в интервале от(–0) до (+0) и полагая, что в конце этого момента времени токи в индуктивностях выровняются,
получаем L1iL (−0) + L2iL |
(−0) = (L1 + L2 )i(+0) . Данное выражение |
1 |
2 |
можно трактовать, как сохранение магнитного потока в контуре до и после
коммутации. |
Отсюда |
независимое |
начальное |
условие |
|
i(+0) = (L1iL |
(−0) + L2iL |
(−0)) /(L1 + L2 ) . Покажите самостоятельно, что |
|||
1 |
|
2 |
|
|
|
при такой коммутации энергия в контуре не сохраняется.
Во второй цепи (см. рис. 5.1.2.) при размыкании ключа в первый момент времени заряды на конденсаторах останутся неизменными и независимые начальные условия определяются вторым равенством в выражении (5.1.1). При замыкании ключа отсутствие между емкостями сопротивления приводит к большим токам, и заряды на емкостях перераспределяются за малый промежуток времени. В электротехнике этим временем пренебрегают. Используя условие сохранения суммарного заряда на емкостях до и после коммутации, а также, что после коммутации напряжение на емкостях будет одинаковым, получаем независимое
начальное uC (+0) = (C1uC (−0) + C2uC |
(−0)) /(C1 +C2 ) , где за время |
1 |
2 |
отсчета взят момент коммутации. Покажите самостоятельно, что при такой коммутации энергия в контуре не сохраняется.
Для расчета переходного процесса обязательно требуется знание независимых начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
5.2.* Расчет переходных процессов классическим методом
Анализ переходного процесса в разветвленной линейной цепи с сосредоточенными параметрами (R, L, C ) классическим методом сводится к решению системы обыкновенных дифференциальных уравнений (ОДУ), составленных на основании законов Кирхгофа для цепи после коммутации
82
(Задача Коши). Решение для каждой ветви записывают для искомой функции (тока, напряжения и т.д.) в виде суммы свободной (решение однородного уравнения) и принужденной (частое решение) составляющих этой функции, т.е.:
i(t) = iсв(t) + iпр(t) , |
(5.2.1а) |
u(t) = uсв(t) + uпр(t) |
(5.2.1б) |
Систему уравнений Кирхгофа преобразуют в систему алгебраических
|
d k |
k |
|
|
уравнений путем замены производных типа |
|
на p |
, а интегралы (если |
|
dtk |
||||
|
|
|
они не исключены предварительным дифференцированием) – на 1/p. Основной объем расчетов связан, во-первых, с нахождением корней (рk) определителя системы, т. е. с нахождением корней характеристического уравнения ∆( p) = 0 , во-вторых, с определением постоянных
интегрирования по начальным условиям. Степень характеристического уравнения не зависит от выбора контуров, для которых составляются уравнения по закону напряжений Кирхгофа. Пусть характеристическое уравнение имеет кратность n. Тогда оно должно иметь и n корней. Поэтому свободный ток (или узловой потенциал) в любой ветви (любом узле) при не кратных корнях определяется выражением
n |
|
iсв(t) = ∑ Ak e pk t , |
(5.2.2) |
k=1
апри кратных корнях, соответственно –
1) случай действительного m –кратного корня (l–й корень имеет кратность m)
|
|
n−m |
m |
|
iсв(t) = |
∑ |
Ak e pk t + e pl t ∑Bk tk −1, |
(5.2.3) |
|
|
|
k =1,k ≠l |
k =1 |
|
2) случай |
комплексно-сопряженных m –кратных корней |
(l–й корень |
||
pl = σl ± jωl, имеет кратность m): |
|
|||
|
|
n−m |
m |
|
iсв(t) = ∑ |
Ak e pk t + eσl t ∑tk −1(M k e jωl t + Nk e− jωl t ) = |
|
||
|
k =1,k ≠l |
k =1 |
|
|
|
n−m |
|
m |
|
= |
∑ Ak e pk t |
+ eσl t ∑tk −1(Bk cosωlt + Ck sin ωlt) = |
(5.2.4) |
|
|
k =1,k ≠l |
|
k =1 |
|
|
n−m |
|
m |
|
= |
∑ Ak e pk t |
+ eσl t ∑tk −1Dk sin(ωlt +ψk ), |
|
|
|
k =1,k ≠l |
|
k =1 |
|
|
|
|
|
83 |
где Ak, Bk, Mk, Nk, Ck, Dk, ψk – постоянные интегрирования. Так как в цепях с пассивными элементами свободные составляющие всегда затухают, то действительные части всех корней должны быть отрицательны, т. е. вcе pi < 0 и σl < 0.
Постоянные интегрирования находят из начальных условий. Количество начальных условий должно быть равно количеству корней с учетом их кратности. Согласно общей теории, развитой для задачи Коши, эти условия задаются значениями искомой функции и ее производных от первого до n - 1 порядка включительно, т. е. знать кроме независимых условий еще так называемые зависимые начальные условия. Для данного случая полная система начальные условий для нахождения констант интегрирования имеет вид
|
|
iсв(0) = i(0) −iпр(0) |
|
|
|||||||||||
|
di |
|
|
|
|
di |
|
|
|
diпр |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||
|
св |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
t =0 |
= dt |
|
t |
=0 − dt |
|
t =0 |
|
|
||||
|
|
|
|
||||||||||||
|
−−−−−−−−−−−− |
(5.2.5) |
|||||||||||||
|
|
|
|||||||||||||
d n−1iсв |
|
|
= |
d n−1i |
− |
d n−1iпр |
|
. |
|||||||
|
|
|
|
|
|
|
|
||||||||
d n−1t |
|
|
d n−1t |
d n−1t |
|||||||||||
|
|
t =0 |
|
|
|
|
t =0 |
|
t =0 |
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||
B (5.2.5) ток iпр (0) и его производные являются принужденными составляющими в первый момент времени после коммутации. Их величины находят либо по установившемуся, стационарному режиму работы схемы (любым способом, рассмотренным в § 3), либо прямым нахождением частного решения, применяя метод вариации произвольных постоянных (метод Лагранжа) или метод Коши.
Ток i(0) и его производные в первый момент времени после коммутации находят из законов коммутации и уравнений Кирхгофа. При этом удобно для нахождения части зависимых начальных условий построить эквивалентную схему. Она получается заменой индуктивностей на идеальные источники тока, дающие ток, равный току в индуктивностях в момент коммутации, и заменой емкостей на идеальные источники напряжения с ЭДС, равными напряжениям на емкостях в момент коммутации. В частности, при нулевых начальных условиях такая замена еще больше упрощает нахождение начальных условий, так как в этом случае индуктивность равносильна разрыву, а емкость – короткому замыканию.
Суммируем основные этапы расчета классическим методом.
1.Рассчитывают токи в индуктивностях и напряжения на емкостях до коммутации.
84
2.Находят по законам коммутации токи в индуктивностях и напряжения на емкостях после коммутации, т. е. определяют независимые начальные условия.
3.Записывают систему дифференциальных уравнений на основе законов Кирхгофа для схемы после коммутации.
4.Находят зависимые начальные условия для токов или напряжений по пункту 3. (Часть зависимых начальных условий удобно находить из эквивалентной схемы.)
5.Ищут частное решение системы неоднородных дифференциальных уравнений пункта 3.
6.Находят решение системы однородных дифференциальных уравнений, т. е. свободное решение.
7.Определяют постоянные интегрирования решения пункта 6.
8.Находят окончательное решение сложением решений п. 5 и п. 6. Проиллюстрируем работу классического метода на примерах
различной сложности.
Пример 5.2.1. Переходный процесс в последовательной R, L цепи.
Положим, что в момент t=0 цепь, состоящая из последовательно соединенных R и L, присоединяется к источнику ЭДС, как показано на рис. 5.2.1. В начале рассмотрим случай постоянного источника с ЭДС равной E. По второму закону Кирхгофа дифференциальное уравнение для
времени t ≥ 0 записывается в виде
|
|
L di + Ri = E |
|
|
|
|
(5.2.6) |
|||
R |
|
dt |
|
|
|
|
|
|
||
Решить |
это |
уравнения |
можно |
прямым |
||||||
K |
L |
|||||||||
интегрированием, используя |
метод |
разделения |
||||||||
|
|
переменных |
|
|
|
|
|
|||
e(t) |
|
|
i |
di' |
R t |
|
' |
|
|
|
|
|
∫ i' − E / R |
= L ∫dt |
|
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
i0 |
|
0 |
|
|
|
|
|
Рис. 5.2.1 |
где интегрирование |
идет от |
момента времени |
|||||||
|
|
сразу после коммутации, когда по закону |
||||||||
коммутации начальный ток в индуктивности |
i0 = 0 . |
Выполнив |
||||||||
интегрирование, получаем |
|
|
|
|
|
|
||||
i(t) = E |
R |
E |
t |
|
|
|
|
|
|
|
(1−e− L t ) = |
(1−e− τ |
) . |
|
|
|
|
(5.2.7) |
|||
R |
|
R |
|
|
|
|
|
|
|
|
Видно, что |
ток в цепи |
экспоненциально затухает. Характерное время |
||||||||
τ = L / R называется постоянной времени R,L цепочки. За это время ток уменьшается в e = 2.71828 раз от своей первоначальной величины.
85
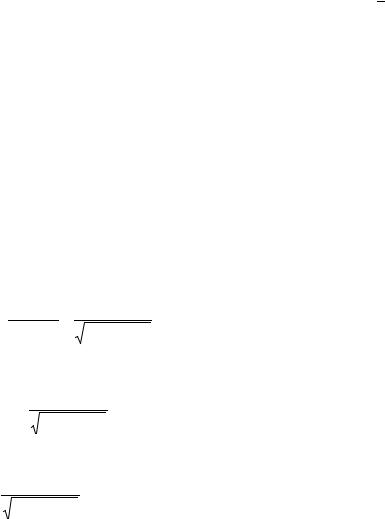
Уравнение (5.2.6), можно решить и по обычным правилам решения обыкновенных дифференциальных уравнений. Если в этом уравнении заменить дифференцирование оператором p, то получим характеристическое уравнение R + pL = 0 , корень которого p = −R / L .
Следовательно, свободный ток, соответствующий решению однородного
уравнения (правая часть в (5.2.1) равна нулю), iсв = Ae pt = Ae− R t
L .
Принужденный ток, являющийся частным решением, равен E / R . Этот ток с физической точки зрения является стационарным током, установившимся после прекращения переходного процесса. Тогда, переходный ток (полное решение дифференциального уравнения) есть сумма этих токов
|
E |
+ Ae− |
t |
|
|
i = |
τ |
(5.2.8) |
|||
R |
|||||
|
|
|
|
Неизвестная постоянная интегрирования A , входящая в это уравнение находится из начального условия: i(0) = i(−0 ) = 0 . Согласно уравнению
(5.2.8) при t=0 имеем 0 = E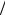
R + A , отсюда A = −E
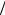R . Окончательно для
переходного тока получаем выражение аналогичное (5.2.7). |
|
|
Усложним этот |
пример, предположив, что источник имеет |
ЭДС |
e(t) = E0 sin(ωt +ψ ) . |
Тогда принужденный ток найдем |
как |
установившийся ток. Этот ток легко находиться методом комплексных амплитуд. Действительно, комплексная амплитуда тока
I = |
E0e jψ |
= |
E0 |
e j(ψ −ϕ) , |
(5.2.8) |
|
R + jωL |
|
R2 +(ωL)2 |
|
|
где φ – аргумент комплексного сопротивления цепи ( tgϕ =ωL / R ). Откуда
iпр(t) = |
|
E0 |
sin(ωt +ψ −ϕ) |
|
(5.2.9) |
|
|
R2 +(ωL)2 |
|
|
|
||
Неизвестная постоянная интегрирования A также находиться из |
||||||
начального |
|
условия |
i(0) = i(−0) = 0 . |
Оно |
дает |
|
A = − |
E0 |
|
sin(ψ −ϕ) . Окончательно переходной ток |
|
||
R2 +(ωL)2
86
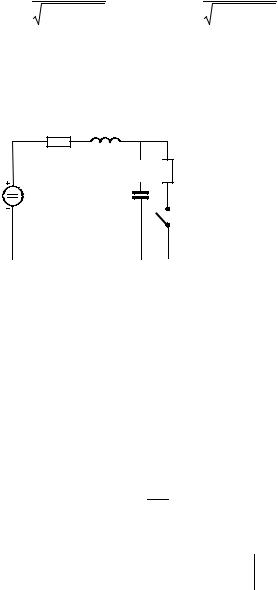
i(t) = |
E0 |
sin(ωt +ψ −ϕ) − |
E0 |
sin(ψ −ϕ)e− |
t |
|
τ |
(5.2.10) |
|||||
|
R2 +(ωL)2 |
|
R2 +(ωL)2 |
|
|
|
Отметим, что выбором момента включения источника можно осуществить условие ψ = ϕ . Тогда будет A = 0 , и в цепи не будет
возникать переходной процесс. Ток сразу после включения будет синусоидальным.
Пример 5.2.2. Найдем ток в цепи, показанной на рис. 5.2.2, после размыкания ключа.
R1 |
L |
R2 |
|
|
|
E |
|
|
|
|
K |
Если ключ замкнут, то напряжение на конденсаторе u0 = ER2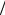 
(R1 + R2 ) , а
ток в индуктивности i0 = E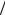
(R1 + R2 ) .
Из законов коммутации следуют
независимые начальные условия i(0) = i0 , u(0) = u0 .
|
|
При размыкании |
ключа начнется |
|
|
изменение заряда на конденсаторе до |
|
|
Рис. 5.2.2 |
||
|
тех пор, пока |
напряжение на |
|
конденсаторе не установиться равным Е0. Закон Кирхгофа в цепи после |
|||
коммутации |
|
|
|
E = Ri + L di |
+uC (t) = Ri + L di |
+ |
1 t |
i(t')dt' +u0 . |
(5.2.11) |
||
|
|
||||||
C ∫ |
|||||||
dt |
dt |
|
|
|
|||
|
|
|
0 |
|
|
||
Решение этого уравнения можно проводить операторным методом, заменяя производную p, а интеграл на 1/p, или методом исключения интеграла дифференцированием уравнения по времени. Выберем второй метод. Тогда уравнение (5.2.11) сведется к однородному дифференциальному уравнению второго порядка
d 2i |
+ 2β |
di |
+ω02i = 0 , |
(5.2.12) |
|
dt2 |
dt |
||||
|
|
|
где β = R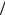
(2L) , ω0 =1
LC . Для решения его кроме начального тока
необходимо знать величину производной тока в первый момент после коммутации (начальные условия задачи Коши), т. е. знать зависимое
начальное условие для производного тока dtdi t =0 . После коммутации цепь
состоит из одного контура и построение эквивалентной цепи не требуется. Искомое зависимое условие получается прямо из уравнения Кирхгофа (5.2.11), в котором надо явно записать известный начальный ток
87
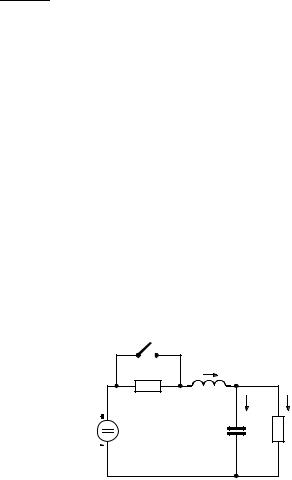
E = u |
0 |
+i R + L di |
|
|
|
(5.2.13) |
|||
|
0 |
|
dt |
|
t =0 |
|
|
||
|
|
|
|
|
|
|
|
||
Тогда, полная система начальных условий |
|
||||||||
|
|
|
= 0, |
|
|
|
|
|
|
i(0) |
|
|
|
|
|
|
|||
|
|
|
|
E −u0 −i0 R |
|
(5.2.14) |
|||
di |
|
|
= |
. |
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
dt |
|
t |
=0 |
|
L |
|
|
||
|
|
|
|
||||||
Характеристическое уравнение, полученное из уравнения (5.2.12), |
|||||||||
p2 + 2βp +ω02 = 0 . |
Оно |
при β <ω0 имеет комплексно-сопряженные |
|||||||
корни |
|
|
|
|
|
|
|
|
|
p1,2 = −β ± j
ω02 − β2 = −β ± jωc ,
где ωc – частота колебаний в контуре. Если добротность контура Q велика, то ω0 ≈ωc . Общее решение однородного уравнения (5.2.12)
|
i(t) = C e p1t |
+ C |
e p2t . |
|
|
|
|
|
|
|
|
|
|
|
|
(5.2.15) |
||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя |
это |
решение |
в |
систему |
уравнений из |
начальных |
условий |
|||||||||||||||
(5.2.14) получаем C1 +C2 = i0 |
, p1C1 + p2C2 = |
|
E −u0 −i0 R |
. |
|
|||||||||||||||||
|
L |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда постоянные интегрирования |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
E −u0 −i0 R / 2 |
1 |
|
|
|
1 |
|
E −u0 −i0 R / 2 |
|
|
|
||||||||||
|
C1 = |
|
|
|
|
|
+ 2 i0 |
, C2 = 2 i0 − |
|
|
|
|
. |
|
(5.2.16) |
|||||||
|
|
2 jωc L |
|
|
|
|
2 jωc L |
|
|
|||||||||||||
Подставив эти постоянные в выражение (5.2.15), и используя формулы |
||||||||||||||||||||||
|
ejωct −e−jωct |
=sin(ω t) , |
ejωct |
+e−jωct |
=cos(ω t) получаем свободное решение |
|||||||||||||||||
|
2j |
|
|
|
c |
|
|
|
|
2 |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
i(t) = |
E −u0 −i0 R / 2 |
e−βt |
sin(ω |
t) +i e−βt |
cos(ω |
t) . |
|
|
(5.2.17) |
||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
ωc L |
|
|
|
|
|
|
c |
|
0 |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как частное решение, то есть, принужденный ток равен нулю, то формула
(5.2.17) является окончательным общим решением задачи.
Пример |
5.2.3. E |
Рассмотрим схему, приведенную на рис. 5.2.3,
K |
i1 |
|
|
R1 |
L |
i3 |
i2 |
|
C |
R2 |
|
|
Рис 5.2.3 |
|
88 |
|
|
|
состоящую из идеального источника постоянного напряжения E=2 кВ, двух сопротивлений R1 = R2 = 100 Ом, индуктивности L = 1 Гн и емкости C = 100 мкФ. Найдем ток в сопротивлении R1 после размыкания ключа.
Решение проведем несколькими способами. В начале будем решать задачу общим способом, используя законы Кирхгофа и вводя токи во всех ветвях. Затем боле простыми с привлечением одного из методов расчета приведенных в § 3.
До момента коммутации при t = 0 ток в индуктивности равен iL(0) = E/R2, а напряжение на емкости равно uC(0) = E, поэтому
независимые начальные условия: iL(0) = i1(0) = 20A, uC(0) = 2кВ. Запишем систему уравнений Кирхгофа после коммутации
|
+ L di1 + |
1 |
t |
|
|
|
i3 (t′)dt′+uC (0), |
|
|||||
E = R1i1 |
|
|||||
C |
|
|||||
|
dt |
∫0 |
|
|
|
|
|
E = R1i1 + L |
di |
+ R2i2 |
, |
(5.2.18) |
|
|
1 |
|||||
|
|
|
dt |
|
|
|
|
i1 = i2 +i3 , |
|
|
|||
|
|
|
|
|
|
|
где токи i1, i2 и i3 – в сопротивлении R1, R2 и емкости. Используя эту систему и независимые начальные условия, найдем недостающие, зависимые начальные условия, необходимые для решения системы Кирхгофа как задачи Коши. Из первого уравнения получаем
di1 |
|
|
= |
1 |
(E − R i (0) −u |
C |
(0)) =–2000 А/c. |
(5.2.19а) |
|
|
|
||||||
dt |
|
t =0 |
|
L |
1 1 |
|
|
|
|
|
|
|
|
|
Далее, учитывая, что напряжение на емкости и на сопротивлении R2 равны, получаем
i2 (0) = uC (0) / R2 = E / R2 =20 А. |
(5.2.19б) |
Это условие можно получить и из второго уравнения системы (5.2.18) с учетом выражения (5.2.19а). Из третьего уравнения системы, используя независимое условие на ток в индуктивности и найденный ток i2(0), получаем
i3 (0) = 0 . |
(5.2.19в) |
Значение производной i2 в первый момент времени после коммутации найдем путем вычитания второго уравнения Кирхгофа из первого с последующим дифференцированием
di2 |
|
= |
i3 (0) |
= 0 . |
(5.2.19г) |
|
CR |
||||
dt |
t =0 |
|
|
|
|
|
2 |
|
|
||
89
Наконец, дифференцируя третье уравнение, находим |
|
||||||||
di3 |
|
|
= di1 |
|
|
− di2 |
|
=–2000 А/c. |
(5.2.19д) |
|
|
|
|||||||
dt |
|
t =0 |
dt |
|
t =0 |
dt |
|
t =0 |
|
|
|
|
|
||||||
Использование эквивалентной схемы удобно лишь для получения зависимых начальных условий на токи в ветвях.
Найдем теперь частное решение, соответствующее установившемуся состоянию схемы. Постоянный ток через емкость не проходит, поэтому i3(∞) = i3пр = 0 и i1(∞) = i1пр = i2(∞) = i2пр = E /(R1 + R2 ) = . 10 А Найдем теперь свободные составляющие тока, являющиеся решением однородной
системы. Заменяя |
|
d |
на |
р и ∫t |
на |
1 |
, |
получим характеристическое |
||||
|
dt |
|
||||||||||
|
|
|
|
|
|
0 |
|
p |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение |
CLR p2 +(CR R + L) p +(R + R ) = 0 из условия равенства |
|||||||||||
|
|
2 |
|
|
|
1 |
2 |
|
1 |
|
2 |
|
нулю определителя матрицы однородной системы |
||||||||||||
|
R1 + Lp |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Cp |
|
|
|
|
|
|
|
|
|||
|
R1 + Lp |
R2 |
|
= 0 . |
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
(5.2.20) |
||||
|
1 |
−1 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения: p1,2 = – 100(1 ± j). Отсюда |
||||||||
Корни |
характеристического |
|||||||||||
решение однородной системы (свободные составляющие токов) имеет вид
i1св
i2св
i3св
(t) = C1e p1t +C2e p2t = C1e(−100+ j100)t (t) = C3e p1t +C4e p2t = C3e(−100+ j100)t (t) = C5e p1t +C6e p2t = C5e(−100+ j100)t
+C2e(−100− j100)t , |
|
+C4e(−100− j100)t , |
(5.2.21) |
+C6e(−100− j100)t . |
|
Постоянные интегрирования найдем из начальных условий (равенства
5.2.19а–д))
di1св
dt
i1св |
= C1 +C2 = i1(0) −i1пр =10A, |
|
|
|
||||
t =0 |
= p1C1 + p2C2 = −100(C1 +C2 ) + j100(C1 −C2 ) = |
(5.2.22) |
||||||
|
|
|
|
|
|
|
|
|
|
= |
di |
− |
di1пр |
= −2000 A |
|
. |
|
|
1 |
|
c |
|
||||
|
|
dt |
t =0 |
dt |
t =0 |
|
|
|
90