
Мищенко А. М. Лекции по электротехнике
.pdf
I |
Z1 |
= |
|
E1 |
. |
|
|
|
(3.3.3) |
|
|
|
|
||||||
|
|
|
Zef 1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
|
|
IE |
= |
|
U |
= |
E1 − Z1I1 |
. |
(3.3.4) |
||
|
Z3 + Z4 |
|
|||||||
|
1 |
|
|
|
Z3 + Z4 |
|
|||
|
|
|
|
|
|
|
|
|
|
Следующий этап: расчет тока |
IE2 , вызванного источником Е2. Он |
||||||||
проводится по схеме, получаемой отсоединением источника тока и замыканием источника Е1 (рис. 3.3.2). Эффективное сопротивление, присоединенное к источнику E2, равно
Zef 2 = Z3 + Z4 + |
Z1Z2 |
. |
(3.3.5) |
|||||
|
||||||||
|
|
|
|
|
|
Z1 + Z2 |
|
|
Поэтому ток IE2 |
с учетом полярности равен |
|
||||||
I |
E2 |
= − |
E2 |
. |
|
|
|
(3.3.6) |
|
|
|
|
|||||
|
|
Zef 2 |
|
|
|
|
||
|
|
|
|
|
|
|
||
Последний |
ток |
II00 рас- |
II0 Z3 |
|||||
считывается |
по |
схеме, |
|
||
приведенной |
на |
рис. 3.3.3. |
|
||
Напряжение на сопротивлении Z4 |
|
||||
|
|||||
равно |
U = II00 |
Zef 3 , |
где |
|
|
|
|||||
эффективное сопротивление Zef3, подсоединенное к идеальному источнику тока. Величину этого сопротивления найдем по формуле
Z1 |
Z2 |
Z4 |
I00 |
Рис. 3.3.3.
|
1 |
|
= |
1 |
+ |
|
|
1 |
|
, |
(3.3.7) |
|
|
|
Z4 |
Z3 |
|
|
|||||||
|
Zef 3 |
|
|
+ Z5 |
|
|||||||
в которой Z5 = Z1Z2 |
(Z1 + Z2 ) . Рассчитав U, искомый ток равен |
|
||||||||||
|
II 00 |
= |
|
U |
. |
|
|
|
(3.3.8) |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
Z3 + Z5 |
|
|
|
|
||||
Наконец, подставив все найденные значения токов в уравнение (3.3.1), получаем искомый ток через сопротивление Z3.
Преимущество данного метода в наглядности – промежуточные алгебраические вычисления, присутствующие в предыдущих методах, заменяются преобразованием схемы.
51
3.4. Метод эквивалентного источника
Этот метод основан на теореме об эквивалентном источнике
(активном двухполюснике).
Теорема Тевенена и Нортона. Любая сколь угодно сложная линейная схема, которая может соединяться с другими схемами только посредством двух узлов, эквивалентна генератору с задающим напряжением, равным напряжению холостого хода и внутренним сопротивлением, равным
входному сопротивлению схемы, или генератору с задающим током,
равным току короткого замыкания, и внутренней проводимостью, равной
входной проводимости схемы.
3.4.1. Теорема об эквивалентном источнике напряжения
Рассмотрим сначала вариант с источником напряжения. Утверждается, что ток в любой ветви mn линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником напряжения. Этот источник напряжения имеет источник ЭДС с ЭДС, равным напряжению на узлах m, n при разомкнутой ветви mn (напряжение холостого хода – Umn) и внутреннее сопротивление равное входному сопротивлению Z0 пассивной цепи со стороны узлов m, n при разомкнутой ветви mn.
Справедливость теоремы вытекает из принципа суперпозиции, согласно которому ток в ветви mn можно рассчитывать как сумму токов в цепях, представляющих последовательную замену исходной цепи схемами, изображенными на рис. 3.4.1. Квадратом изображена цепь, к которой подсоединена ветвь mn. Буква А в квадрате обозначает, что в цепи имеются активные элементы (источники напряжения и тока), а буква П показывает, что цепь состоит только из пассивных элементов.
Включим последовательно в ветвь mn навстречу друг другу два одинаковых источника ЭДС. Это включение согласно закону Ома не изменит ток в ветви mn. Полученную схему представим в виде суперпозиции двух схем (центральная часть рисунка). Первая схема состоит из исходной цепи и ветви mn с включенной в ней дополнительной ЭДС. Вторая – из исходной цепи с выключенными внутренними источниками и ветви mn с включенной в ней другой дополнительной ЭДС. Выключение источников в исходной цепи осуществляется по правилам
52
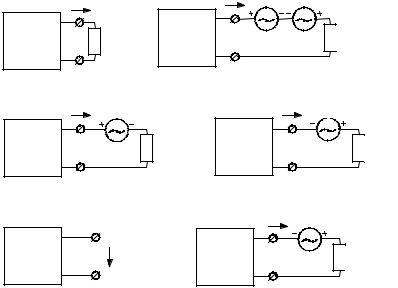
расчета методом суперпозиции,
|
i |
|
|
i Umn |
|
Umn |
|
А |
m |
Zmn = |
А |
m |
|
|
Zmn |
|
|
|
|||||
|
n |
|
|
n |
|
|
|
|
i = 0 |
Umn |
|
|
|
i |
Umn |
А |
m |
|
Zmn + |
|
П |
m |
Zmn |
|
|
|
|
||||
|
n |
|
|
|
|
n |
|
|
|
|
|
|
i |
|
Umn |
А |
m |
Umn |
+ |
П |
m |
|
Zmn |
|
|
|
|||||
|
n |
|
|
|
n |
|
|
Рис 3.4.1
т. е. вместо источников оставляют их внутренние сопротивления. Ток в ветви mn будет равен сумме токов этих двух схем. Выберем теперь дополнительную ЭДС такой, чтобы ток в ветви mn в первой схеме стал равен нулю. Это можно осуществить при дополнительной ЭДС, равной напряжению холостого хода на зажимах mn с обратным знаком (–Umn). Тогда дополнительная ЭДС во второй схеме будет равна Umn. Такой выбор дополнительной ЭДС приводит к тому, что первая схема эквивалентна разрыву, а ток во второй схеме будет равен току ветви mn в исходной схеме (схематично это отражено в нижней части рисунка). Теорема доказана. Таким образом, ток в ветви mn может быть рассчитан по простой схеме, состоящей из источника напряжения имеющего ЭДС, равную Umn, и внутреннее сопротивление Z0, равное сопротивлению пассивной электрической цепи со стороны ветви mn, т. е.
Imn = |
Umn |
, |
(3.4.1) |
|
Zmn + Z0 |
||||
|
|
|
где Zmn -сопротивление ветви mn.
53
Расчеты данным методом можно проводить одновременно для двух и |
||||||||||||||||||||
более ветвей сложной активной цепи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пример 3.4.1. Рассчитаем ток в сопротивлении Z3 методом |
|||||||||||||||||||
эквивалентного генератора в схеме, изображенной на рис. 3.1.3. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
|
|
U2 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
Z2 |
|
|
I00 |
|
|
|
Z4 |
Z1 |
Z2 |
|
Z4 |
|
E1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
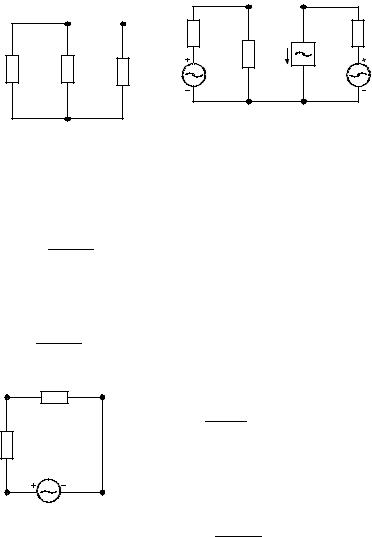
Рис. 3.4.3. |
|
|
|
|
|
Рис. 3.4.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем внутреннее сопротивление вводимого эквивалентного |
||||||||||||||||||||
источника напряжения Z0 по схеме, приведенной на рис. 3.4.2. Эта схема |
||||||||||||||||||||
получена из исходной схемы удалением сопротивления Z3 и исключением |
||||||||||||||||||||
источников: источник тока отсоединяется, источник напряжения |
||||||||||||||||||||
замыкается. Величина сопротивления цепи между точками 1 и 2 равна |
||||||||||||||||||||
Z0 |
= Z4 + |
|
Z1Z2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.4.2) |
||
|
|
Z1 + Z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Напряжение холостого хода рассчитывается по схеме, изображенной на |
||||||||||||||||||||
рис. 3.4.3. Потенциалы U1 и U2, возникающие в местах отсоединения |
||||||||||||||||||||
сопротивления Z3, рассчитываются по формулам |
|
|
|
|
|
|
||||||||||||||
U1 = Z2 Z |
|
E1 |
, |
U2 = E2 + Z4 I00. |
|
|
|
|
|
|
|
|
|
|
|
(3.4.3) |
||||
1 |
+ Z |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z3 |
|
|
Рассчитав |
|
U1 |
|
и |
U2, |
|
напряжение |
|
холостого |
||||||
|
|
|
|
|
хода находят как |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
U |
xx |
=U −U |
|
= |
Z |
|
1 |
[Z E −(Z +Z |
|
)E |
|||||
|
|
|
|
|
|
1 |
2 |
|
|
|
+Z |
2 |
2 1 |
1 |
2 |
|
2 (3.4.4) |
|||
Z0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
−Z4 (Z1 +Z2 )I00]. |
|
|
|
|
|
|
|
|
|
|||||||
|
Uxx |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Окончательная |
эквивалентная |
схема |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
изображена на рис. 3.4.4. Из этой схемы |
|||||||||||||||
|
Рис. 3.4.4. |
непосредственно следует |
|
|
|
|
|
|
||||||||||||
|
|
|
Iz3 |
|
= |
|
U xx |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Z3 + Z0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
54
(3.4.5)
Расчет с помощью эквивалентного генератора наиболее удобен для быстрой оценки токов в ветвях.
3.4.2. Теорема об эквивалентном источнике тока
Эта теорема утверждает, что ток в любой ветви mn линейной электрической цепи не изменяется, если электрическую цепь, к которой подключена ветвь, заменить эквивалентным источником тока; ток этого источника должен быть равен току, проходящему между узлами m и n, замкнутыми накоротко, а внутренняя проводимость источника должна равняться входной проводимости пассивной электрической цепи со стороны узлов m и n при разомкнутой ветви mn.
Справедливость теоремы основывается на эквивалентном преобразовании источника напряжения в источник тока. В соответствии с теоремой об эквивалентном источнике напряжения приведем исходную схему к простой, состоящей из источника напряжения, имеющего ЭДС, равную напряжению холостого хода Umn, и внутреннее сопротивление Z0. Данный источник напряжения преобразуем в эквивалентный источник тока с
I |
0mn |
= Umn = Y U |
mn |
. |
(3.4.6.) |
|
0 |
|
|
||
|
|
Z0 |
|
|
|
Этот ток равен току, проходящему через короткозамкнутые узлы mn, поэтому ток через ветвь mn можно рассчитать как
I |
|
= |
Z0Zmn |
I |
|
1 |
= |
|
|
Z0 |
|
I |
|
= |
|
Ymn |
I |
0mn |
, |
(3.4.7) |
||||
mn |
|
0mn Z |
|
Z |
|
+ Z |
|
0mn |
Y |
+ Y |
||||||||||||||
|
|
Z |
0 |
+ Z |
mn |
|
mn |
|
0 |
mn |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
mn |
|
|
|
|
|||||
где Ymn = 1/Zmn, Y0 = 1/Z0.
Расчеты данным методом можно проводить одновременно для двух и нескольких ветвей сложной активной схемы.
55
§ 4. Резонанс в электрической цепи
Изменение частоты источника или параметров схемы может приводить к появлению резонансных явлений, когда величины токов или напряжений достигают экстремальных значений. Резонансные явления играют важную роль в работе электрических цепей. На их основе работают системы передачи и приема информации, узкополосные фильтры и т. п. Цепи, содержащие емкостные и индуктивные сопротивления и работающие в области резонанса, называются резонансными цепями или колебательными контурами. Принято разделять колебательные контуры на два типа: последовательный колебательный и параллельный колебательный контур. Такое разделение условно связано со способом подключения резонансной цепи к источнику электрической энергии. Если после соединения источника с цепью ветви с емкостью и индуктивностью образуют с источником замкнутый контур, то данная цепь называется последовательным колебательным контуром. Если источник при подсоединении к цепи оказывается параллельно подключенным к ветви с емкостью и к ветви с индуктивностью, то такая цепь называется параллельным колебательным контуром. Ниже рассматриваются резонансные явления в пассивных цепях на примере простейших последовательных и параллельных контуров. В таких контурах наиболее ярко проявляются физические процессы, лежащие в основе резонансных явлений и позволяющие использовать их в качестве узкополосных фильтров и согласующих элементов между источником и нагрузкой. Для описания работы колебательного контура используются параметры: резонансная частота контура, собственная частота контура, характеристическое (волновое) сопротивление контура, добротность и др. Определим эти параметры как методом комплексных амплитуд, так и прямым анализом дифференциальных уравнений (физический способ).
4.1. Последовательный колебательный контур. Резонанс напряжений
4.1.1. Метод комплексных амплитуд определения параметров контура
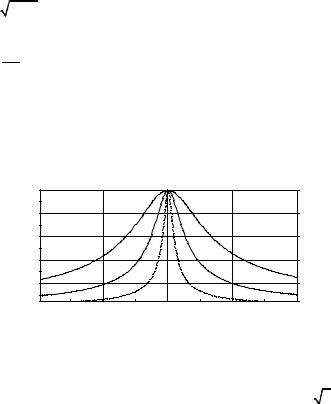
Метод комплексных амплитуд определения параметров контура основан на расчете его комплексного сопротивления. Рассмотрим простую цепь из последовательно соединенной индуктивности, емкости и сопротивления. Подключим эту цепь к идеальному источнику синусоидального
напряжения E(t) = Em sin(ωt +ψ) (рис. 4.1.1). Получился замкнутый
контур, поэтому цепь называют последовательным колебательным контуром. Найдем ток в контуре методом комплексных амплитуд из алгебраического уравнения
56

Emejψ =Z( jω)I =(R+ jωL+ jω1C)I = Zejψ0 I = R2 +(ωL−ω1C)2ejψ0 Imejψ1 , (4.1.1)
R2 +(ωL−ω1C)2ejψ0 Imejψ1 , (4.1.1)
где ψ0 – аргумент комплексного сопротивления |
|
|||
tgψ0 |
= |
ωL −1/ωC |
, |
(4.1.2) |
|
|
R |
|
|
R |
ψ1 |
– фаза тока. |
L |
Комплексная амплитуда тока равна |
|
|
|
|
|
|
|
|
I |
= E |
= |
|
|
1 |
E |
|
1 |
= |
|
E |
|
|
|
C |
|
Z |
R(1+ j |
(ωL − |
)) |
||||||
|
|
|
|
|
R |
ωC |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
E exp(jψ) |
|
|
|
|
||||
|
|
|
|
|
= |
R(1 |
m |
ω |
− |
ω |
= |
|
|
||
|
|
Рис. 4.1.1 |
|
|
+ jQ( |
ω |
|
0 )) |
|
|
|||||
|
|
|
|
|
|
|
|
ω |
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
= Em |
|
|
1 |
|
exp( j(ψ −ψ 0 )) = |
|
|
|
|
|
|
||||
R |
|
1 + Q 2 ( |
ω − |
ω0 |
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
ω |
|
|
|
|
|
|
|
|
|
|
(4.1.3) |
Em |
|
1 |
exp( jψ1 ) = Im e jψ1 , |
|
|
|
|
|
|
|
|
|
|||
R |
1 + Q 2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im = |
Em |
1 |
, |
|
|
|
|
|
|
|
|
|
|
(4.1.4) |
|
R 1 + Q2 x2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
амплитуда тока. Мгновенный ток – i(t) = Im sin(ωt +ψ1) . Сдвиг фаз (или
разность фаз) между током и напряжением обусловлен комплексным сопротивлением контура. В данных обозначениях он записывается как
tg(ψ1 |
−ψ ) = − |
ωL −1/ωC |
= −Qx . |
(4.1.5) |
|
|
R |
|
|
В равенстве (4.1.3) введены следующие параметры:
ω0 = 1 LC |
(4.1.6 а) |
– собственная частота контура; |
|
Q = L / C R = ρ / R |
(4.1.6 б) |
57
– добротность последовательного контура; |
|
|
|
||||||
ρ = |
L / C |
|
|
|
|
(4.1.5 в) |
|||
– волновое сопротивление контура; |
|
|
|
|
|||||
x = ( |
ω − |
ω0 ) |
|
|
|
|
(4.1.6 г) |
||
|
ω0 |
|
ω |
|
|
|
|
|
|
– относительная расстройка. |
|
|
|
|
|
||||
При ω = ω0 амплитуда тока имеет максимальное резонансное значение |
|||||||||
Imo = Em / R , |
поэтому |
эту |
частоту |
еще |
называют |
резонансной. |
На |
||
рис. 4.1.2 приведены резонансные кривые тока для Q = 150 – пунктирная |
|||||||||
линия, Q = 50 – сплошная тонкая, Q = 20 – жирная линия. |
|
||||||||
|
I |
1 |
|
|
|
|
|
|
|
|
---- |
|
|
|
|
|
|
|
|
|
I 0 |
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
---- |
|
|
|
|
|
0.95 |
1 |
|
1.05 |
_f 0 |
|
|
|
|
|
|
1.1 |
|
|||
Рис.4.1.2.
При увеличении добротности контура частотная характеристика тока сужается (см. рис. 4.1.2.). По ширине частотной зависимости Im определяют полосу пропускания контура 2∆ω = 2(ω −ω0 ) . Условились
считать, что она определяется шириной спектра на уровне 1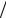 2 0,707 от максимального (резонансного) значения. В области ω0 относительную расстройку можно рассчитывать как x ≈ 2∆ω
2 0,707 от максимального (резонансного) значения. В области ω0 относительную расстройку можно рассчитывать как x ≈ 2∆ω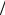 ω0 . Если спектр амплитуды
ω0 . Если спектр амплитуды
тока достаточно узкий, такой, что в этой области частот он спадает до указанных значений, то полосу пропускания контура, можно связать с добротностью контура простым выражением
2∆ω |
= |
1 |
. |
(4.1.7) |
|
|
|||
ω0 |
Q |
|
||
Врадиотехнике обычно имеют дело с контурами большой добротности
≥102, поэтому эта формула часто используется для взаимного определения полосы пропускания и добротности. Согласно выражению (4.1.6 б)
получаем 2∆ω /ω0 = R / ρ . Откуда следует, что увеличение сопротивления контура расширяет полосу пропускания контура.
58
При резонансной частоте ω = ω0 разность фаз ψ0 =ψ1 −ψ между
током и приложенным к контуру напряжением равна нулю. Обычно говорят, что ток и напряжение в цепи находятся в фазе. Это условие в радиотехнике используется для определения резонансных частот последовательного колебательного контура. Математически оно соответствует требованию равенства нулю реактивной части полного
комплексного |
сопротивления |
контура |
|
Im Z ( jω0 ) = 0 . |
|
Для |
|||||||
рассматриваемого |
контура |
|
комплексное |
сопротивление |
равно |
||||||||
Z = R + jωL +1 jωC . |
Поэтому, |
это условие будет выполняться, когда |
|||||||||||
|
|
|
|
|
|
ω0 L =1 ω0C , т. |
е. при ω0 =1 |
|
|
. |
|||
|
|
|
|
|
|
|
LC |
||||||
|
|
|
|
|
|
Отсюда, согласно уравнению (4.1.1), |
|||||||
|
|
|
|
|
|
сразу |
получается |
резонансная |
|||||
|
|
|
|
|
|
амплитуда тока Imo = Em |
R . При этой |
||||||
|
|
|
|
|
|
частоте напряжение на емкости |
|
|
|
||||
|
Рис. 4.1.3 |
|
|
|
UC = Imo jω0C = − jEmQ |
|
|
|
|||||
|
|
|
|
и на индуктивности |
|
|
|
|
|||||
|
|
|
|
|
|
UL = jω0 LImo = jEmQ . |
|
|
|
||||
|
|
|
|
|
|
Видно, что они равны и находятся в |
|||||||
противофазе (имеют разные знаки). |
|
|
|
|
|
|
|
||||||
Поэтому |
о |
|
резонансе |
|
в |
|
|
|
|
|
|
|
|
последовательном контуре принято |
|
|
|
|
|
|
|
||||||
говорить |
как |
|
о |
резонансе |
|
|
|
|
|
|
|
||
напряжений. |
На |
векторной |
|
|
|
|
|
|
|
||||
диаграмме (рис. 4.1.3) наглядно |
|
|
|
|
|
|
|
||||||
видно отсутствие |
разности |
фаз |
|
|
|
|
|
|
|
||||
между током и напряжением, так |
|
|
|
|
|
|
|
||||||
как векторы тока и напряжения |
|
|
|
|
|
|
|
||||||
коллинеарные, а сдвиг по фазе |
|
|
|
|
|
|
|
||||||
между ними 1800. |
|
|
|
|
|
|
|
|
|
|
|
|
|
На |
рис. 4.1.4 |
показаны |
|
|
|
|
|
|
|
||||
амплитудно-частотные |
характеристики |
(АЧХ) |
напряжения |
|
на |
||||||||
конденсаторе – тонкая сплошная линия, на емкости – жирная линия, на индуктивности – пунктирная линия. Параметры контура: L = 0,25 мГн, С = 1 мкФ, R = 6,8 Ом, Q = 2,5, E = 1 B. Напряжения на емкости и индуктивности при ω = ω0, хотя и в Q раз больше приложенного напряжения, тем не менее, они не максимальны. Максимальная амплитуда
напряжения на емкости достигается при ωC =ω0  1−1 2Q2 , а на индуктивности – при ωL =ω0
1−1 2Q2 , а на индуктивности – при ωL =ω0 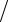

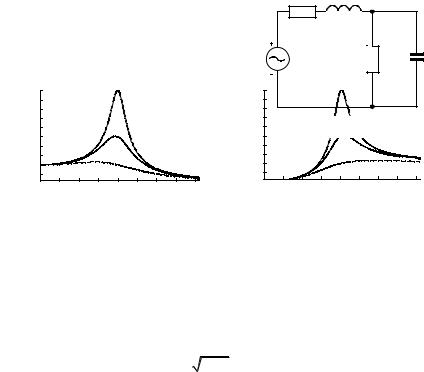
 1 −1
1 −1 2Q2 . Частоты ωC и ωL также можно
2Q2 . Частоты ωC и ωL также можно
59
считать резонансными частотами. Однако в радиотехнике их не считают |
|||||||||||
резонансными, |
так как они не удовлетворяют условию Im Z ( jω0 ) = 0 . |
||||||||||
Это связано с тем, что из-за использования в радиотехнике контуров с |
|||||||||||
большой добротностью вообще не возникает потребности в выделении |
|||||||||||
данных частот, так как практически нет различы между ωC и ωL или ω0. |
|||||||||||
Например, |
при |
Q = 100 частоты |
ωC и ωL |
отличаются от ω0 всего на |
|||||||
≈ 2 10−3 % . С уменьшением добротности максимумы в спектрах UC |
|
и UL |
|||||||||
размываются до полного |
ис- |
|
|
|
|
|
|
|
|||
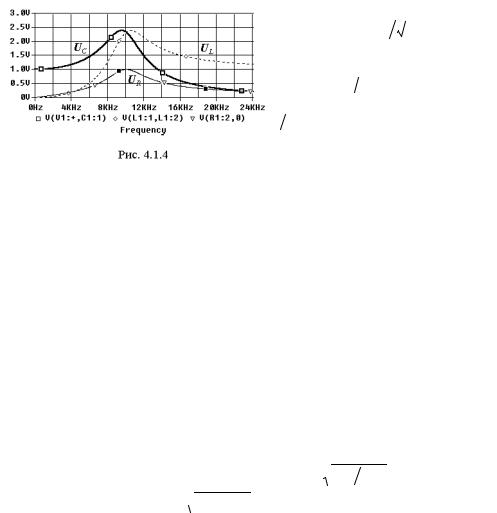
чезновения. На рис. 4.1.5 приведены |
|
|
|
|
|
|
|||||
частотные |
|
|
характеристики |
|
R |
L |
|
|
|
||
напряжений |
на |
емкости |
и |
|
|
|
|
||||
индуктивности |
для |
трех |
значений |
|
|
|
|
|
|
||
добротности Q = 1, 2.5 и 5. Отметим, |
|
|
|
|
|
|
|||||
что мощность, вводимая в контур, а, |
E |
|
R1 |
C |
|
|
|||||
следовательно, |
и |
рассеиваемая |
в |
|
|
|
|||||
UKCC5 |
|
Q = 5 |
|
|
UKLL 5 |
|
Q = 5 |
|
|
||
4 |
|
|
|
|
|
4 |
|
|
|
|
|
3 |
|
------ Q = 2.5 |
|
3 |
|
Рис. 4.1.6 |
Q = 2.5 |
|
|||
2 |
|
|
2 |
|
------ |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
1 |
Q = 1 |
|
|
|
f |
1 |
|
|
Q = 1 |
|
f |
|
|
|
--- |
|
|
|
|
--- |
|||
|
0.5 |
1 |
1.5 |
2 |
f0 |
|
0.5 |
1 |
1.5 |
2 |
f0 |
Рис. 4.1.5.
нем, максимальна при максимальном токе, т. е. при ω = ω0.
Внутреннее сопротивление источника напряжения складывается с сопротивлением ненагруженного контура. Поэтому последовательные резонансные контуры обычно используют с источниками напряжения, для которых активное сопротивление много меньше активного сопротивления контура. Это позволяет избегать расширения полосы пропускания контура.
Пример 4.1.1. Для схемы приведенной на рис. 4.1.6 найдем резонансную частоту, добротность контура и полосу пропускания. При
условии ρ / R1 << 1, где ρ = L / C – волновое сопротивление. В этой
схеме идеальный источник напряжения E питает колебательный контур, состоящий из сопротивления R, индуктивности и емкости с потерями, представленными параллельно включенным резистором R1. В контуре источник напряжения, емкость и индуктивность, несмотря на сопротивление R1, образуют последовательный контур и, следовательно, цепь является последовательным колебательным контуром.
60
