5.3.5. Вносимое затухание четырёхполюсника

Вносимое затухание (или усиление) является мерой оценки изменения условий передачи при включённом четырёхполюснике между источником и приёмником. Пусть между источником напряжения с Z₁ и приёмником с Z₂ включён четырёхполюсник. Под вносным затуханием четырёхполюсника подразумевается или 10-кратное значение относительно мощности S₁, которую непосредственно отдавал бы источник сопротивлению Z₁ к мощности S₂ на выходе четырёхполюсника, нагруженного сопротивлением Z_2.

(1)

Мощность выражается:

; Согласно (1):

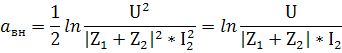
Отношение может быть выражено через характеристические параметры четырёхполюсника и Z₁ и Z₂

Пользуясь уравнениями четырёхполюсника в форме А, находим

откуда следует:

(3)

Рис. 5.20

На основании приведённых выше формул:

; ;

; (4)

Подстановка (4) в (3) даёт:

После алгебраических преобразований получим:

, где

и называются коэффициентами отражения на входе и выходе четырёхполюсника. Окончательно:

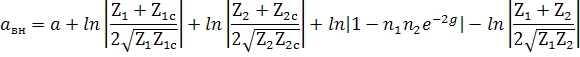
Вносимое затухание состоит из 5 слагаемых: 1 – собственное затухание четырёхполюсника; 2 – затухание вследствие несогласованных сопротивлений на входе четырёхполюсника; 3 – то же на выходе; 4- затухание вследствие взаимодействия несогласованностей на входе и выходе и 5 – затухание вследствие несогласованности сопротивления источника и приёмника. В случае согласованного включения сопротивлений на входе и выходе четырёхполюсника, то есть Z₁ = Z_1c и Z₂ = Z_2c равно собственному затуханию четырёхполюсника. Если а_вн = 0, это значит S₁ = S₂.

Если сопротивление Z₂ = Z₁ затухание называется рабочим

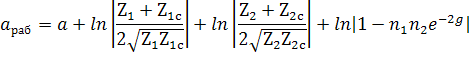
5.3.6. Соединения четырёхполюсников

Уравнения четырёхполюсников в Y, Z, A-параметрах в матричной форме:

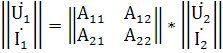
Такие записи удобны при анализе различных соединений четырёхполюсников.

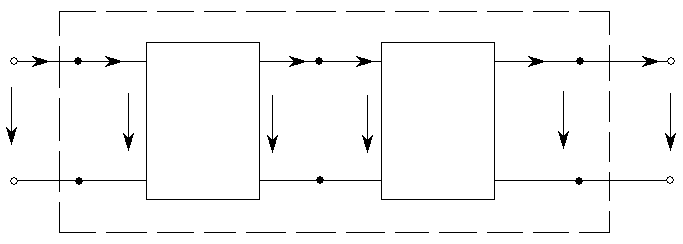
Рассмотрим каскадное соединение двух четырёхполюсников, их вместе можно рассматривать как один эквивалентный четырёхполюсник.

Рис. 5.21

; - на входе; ; - на выходе

В данном случае: ; ; ; .

Задача: определить параметры эквивалентного четырёхполюсника через параметры 1 и 2 четырёхполюсников.

Равенства и определяют целесообразность системы уравнений.

В матричной форме имеем:

; ; .

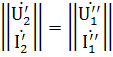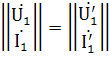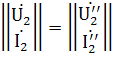При этом лучше всего использовать уравнения в А-параметрах:

;

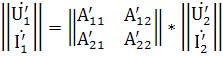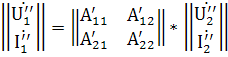
Используя эти соотношения получим:

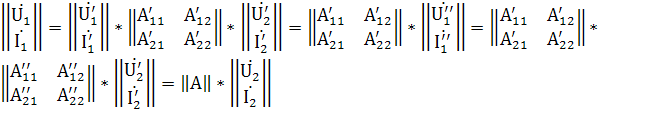
Таким образом, матрица А-параметров двух четырёхполюсников равна произведению матриц А-параметров отдельных четырёхполюсников. Произведя эту операцию, получим:

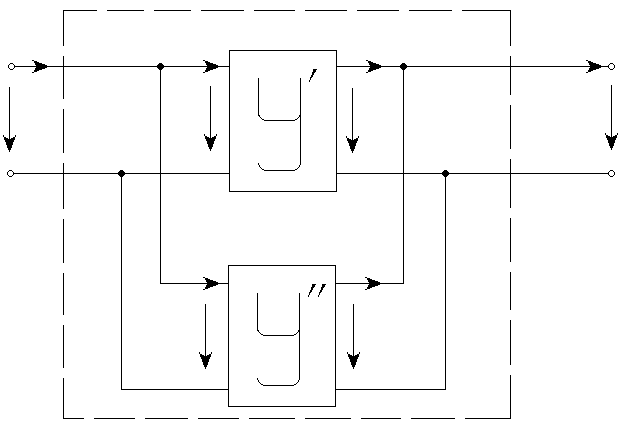
Рассмотрим теперь параллельное соединение. При этом имеет место:

; или в матричной форме:

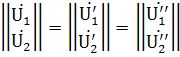
Рис. 5.22

Поэтому в качестве исходной системы уравнений следует выбрать ту, в которой токи выражены через напряжения, т.е. систему Y-параметров. Имеем:

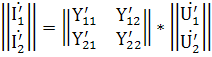и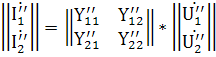

Так как и , то:

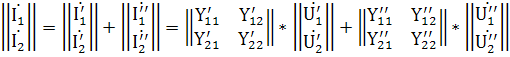
Имея в виду равенство матриц напряжений, получаем:

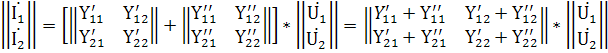
Следовательно, матрица Y-параметров есть сумма матриц Y-параметров отдельных четырёхполюсников.

Рассмотрим последовательное соединение 2-х четырёхполюсников. При таком соединении имеем: ; и ;

Целесообразно воспользоваться уравнениями четырёхполюсника в Z-параметрах.

Рис. 5.23

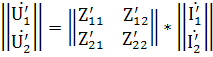и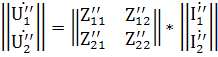

Получаем:

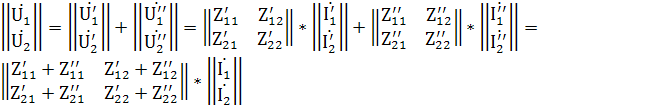
Таким образом, при последовательном соединении 2-х четырёхполюсников матрица Z-параметров эквивалентного четырёхполюсника равна сумме матриц Z-параметров отдельных четырёхполюсников.