
- •Приклади виконання завдань Модуль1. Статика твердого тіла
- •Розв”язання.
- •3. Просторова система сил
- •ЗавданняС4. Зведення системи сил до найпростішого виду
- •Завдання с5.Визначення реакці опор твердого тіла( плита, вал )
- •2.Для визначення шести невідомих реакцій складаємо шість рівнянь рівноваги діючої на плиту просторової системи сил :
- •Відповідь :
- •Розв”зання:
3. Просторова система сил
ЗавданняС4. Зведення системи сил до найпростішого виду
Визначити
голвний
вектор
![]() і
головний момент
і
головний момент
![]() просторової
системи
сил
відносно
центра О, а також установити, до якога
най-
простішого
виду зводиться задана система сил.
Напрямки
дії
сил
пока-
зано
на рисунках
Модулі
сил i
геометричні
розміри
наведені
в таблиці
до завдання
просторової
системи
сил
відносно
центра О, а також установити, до якога
най-
простішого
виду зводиться задана система сил.
Напрямки
дії
сил
пока-
зано
на рисунках
Модулі
сил i
геометричні
розміри
наведені
в таблиці
до завдання
Приклад.
Уздовж сторін
паралелепіпеда
(рисС3.1)
діють
чотири
сили,
модулі
яких
![]() =
20 Н,
=
20 Н,
![]() =
30
Н, F
=
30
Н, F![]() =
40
Н, F4
- 50
Н.
=
40
Н, F4
- 50
Н.
Звести цю систему сил до найпростішого виду, якщо а= 3 м, Ь = 6 м, с = 2 м.
Р о з в
' я з а нн и я.
Головний вектор i
головний момент
системи
сил
визначаютъся
виразами
![]() =
=![]()
![]() ;
;
![]() =
=
![]()
![]() (
(![]() ).
).
Окремі випадки зведения:
-
якщо
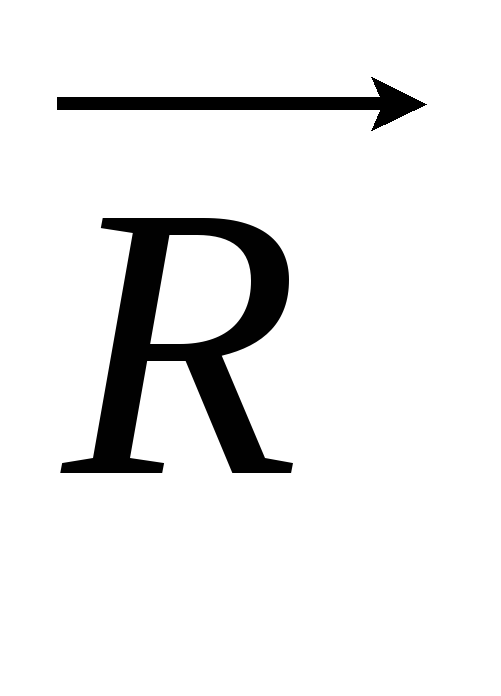 ≠
0
та
≠
0
та
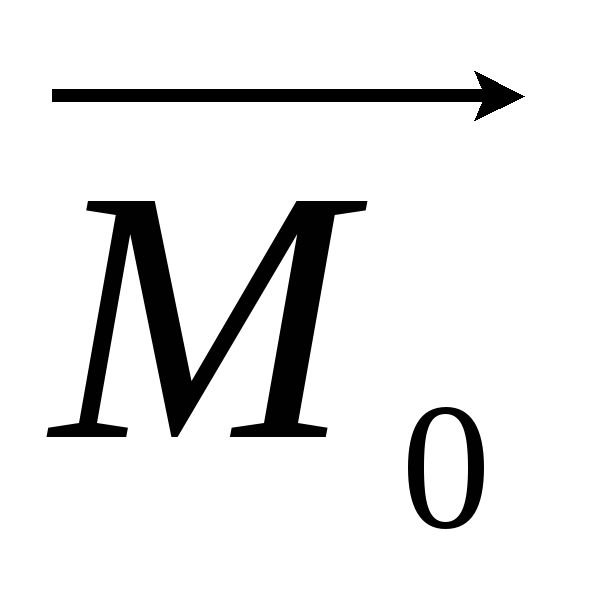 =
0, то система сил
еквівалентна
одній
силі
(тобто
рівнодійні),
яка
гуометрично
дорівнює
головному век-
тору
i
прикладена
в центрі
О.
Напрямок
рівнодійної
проходить через центр О;
=
0, то система сил
еквівалентна
одній
силі
(тобто
рівнодійні),
яка
гуометрично
дорівнює
головному век-
тору
i
прикладена
в центрі
О.
Напрямок
рівнодійної
проходить через центр О;
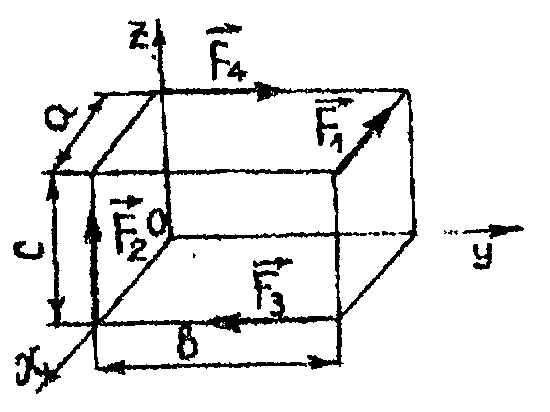 Рис.С4
Рис.С4
2)
коли
![]() =
0
та
=
0
та
![]() ≠
0,
то система сил зводиться
до одиіеї
пари сил; 3) якщо
≠
0,
то система сил зводиться
до одиіеї
пари сил; 3) якщо
![]() ≠
0
i
≠
0
i
![]() ≠
0,
але
≠
0,
але
![]() ┴
┴
![]() (
(![]() .
.
![]() =
0), то
система сил зводиться до рівнодійної,
напрямок
якої
не проходить через центр зведення О; 4)
коли
=
0), то
система сил зводиться до рівнодійної,
напрямок
якої
не проходить через центр зведення О; 4)
коли
![]() ≠
0
та
≠
0
та
![]() ≠
0
але
вектор
≠
0
але
вектор
![]() колінеарний
до
колінеарний
до
![]() ,
то
система сил зводиться
до
,
то
система сил зводиться
до
силового
гвинта (динами); 5) якщо
![]() =
0
i
=
0
i
![]() =
0
то система сил зна-
ходиться
в pівновазі.
=
0
то система сил зна-
ходиться
в pівновазі.
У вибраній системі координат (див. рис.4) головний вектор
R=![]() ,
,
де
Rx
=
![]() Fix
= - F1
= -20 kH;
Fix
= - F1
= -20 kH;
Ry
=
![]() Fiy
= F4 –
F3 =
10 kH;
Fiy
= F4 –
F3 =
10 kH;
Rz
=
![]() Fiz
= F2
= 30 kH;
Fiz
= F2
= 30 kH;
R =
![]() =
37,5 kH
=
37,5 kH
а головний момент
Mo=
![]() ,
,
![]() =
=
![]() М
М![]() (
(
![]() )
= 0,
-
)
= 0,
-![]()
![]() c
=
-50
c
=
-50
![]() 2
= -100 Нм
2
= -100 Нм
![]() =
=![]() М
М![]() (
(
![]() )
= 0,
-
)
= 0,
-![]()
![]() c
-
-
c
-
-![]()
![]() а
=
-20
а
=
-20![]() 2
- 30
2
- 30![]() 3
= -130 Нм
3
= -130 Нм
![]() =
=![]() М
М![]() (
(
![]() )
=
)
=
![]()
![]()
![]() -
-![]()
![]()
![]() а =
20
а =
20![]() 6
- 40
6
- 40![]() 3
= 0
3
= 0
![]() =
=
![]() =
10
=
10![]() = 164 Нм
= 164 Нм
Напрямні косинуси цих векторів визначаються виразами :
cos(![]() ^O
^O![]() )
=
)
=
![]() =
=
![]() =
-20 / 37,5 = -0,533;
=
-20 / 37,5 = -0,533;
cos(![]() ^O
^O![]() )
=
)
=
![]() =
=
![]() =
10 / 37,5 = 0,263 ; cos(
=
10 / 37,5 = 0,263 ; cos(![]() ^O
^O![]() )
=
)
=
![]() =
=
![]() =
30 / 37,5 = -0,8;
=
30 / 37,5 = -0,8;
cos(![]() ^O
^O![]() )
=
)
=
![]() =
=
![]() =
-100/ 164 = -0,609 ;
=
-100/ 164 = -0,609 ;
cos(![]() ^O
^O![]() )
=
)
=
![]() =
=
![]() =
-130/ 164 = -0,793 ;
=
-130/ 164 = -0,793 ;
cos(![]() ^O
^O![]() )
=
)
=
![]() =
=
![]() =0;
=0;
Головний вектор і головний
момент не дорівнюють нулеві і утворюють
між собою кут
![]() , що визначається виразом :
, що визначається виразом :
cos![]() =
=
![]() =
=
![]() =
0.114
=
0.114
Система сил зводиться до
динами (силового гвинта),тобто до
![]() (головного
вектора) і пари сил із моментом
(головного
вектора) і пари сил із моментом
![]() =
=
![]() cos(
cos(![]() ,
,![]() )
=
)
=
![]() = 18,7 Нм
= 18,7 Нм
Рівняння прямої дії динами (центральної гвинтової осі)мають вигляд :
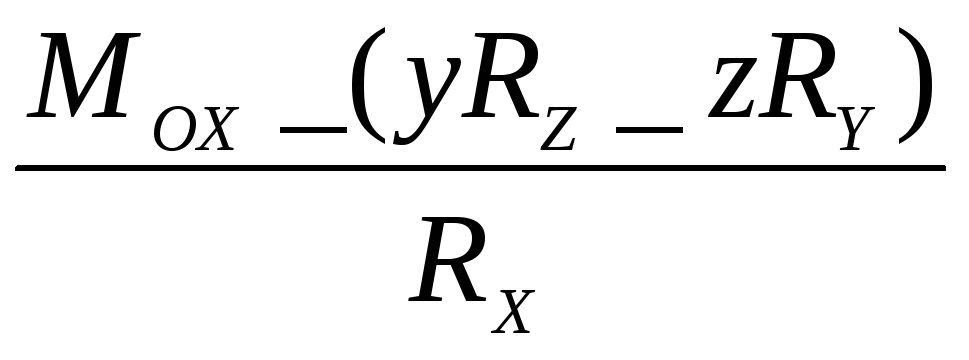 =
=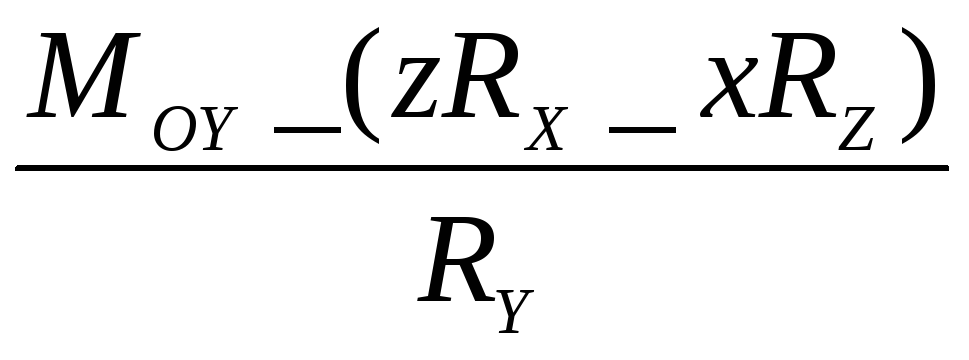 =
=
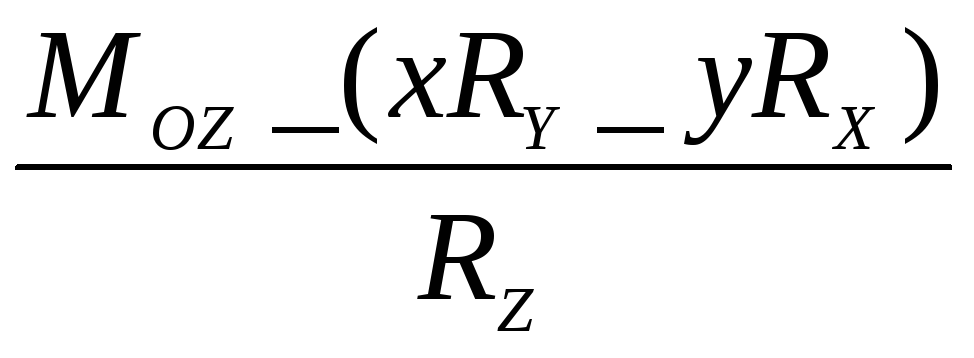
де
![]() -
біжучі координати точки , що лежить на
цій гвинтовій осі.
-
біжучі координати точки , що лежить на
цій гвинтовій осі.
Підставляючи відповідні величини в рівняння центральної лінії дістанемо
![]() =
=![]() =
=
![]()
Таким чином , центральна вісь має вигляд прямої типу двох площин:
6![]() -
3
-
3![]() +5
+5![]() -36
= 0 ; 10
-36
= 0 ; 10![]() +2
+2![]() +
+![]() -39
= 0
-39
= 0
Завдання с5.Визначення реакці опор твердого тіла( плита, вал )
Задача 5.1.
Прямокутні
плити,
на які
діють
сили
![]() ,
,
![]() i
пара сил із
моментом М,
i
пара сил із
моментом М,
закріплено відповідним способом, показаним на схемах (рис. )
Значення сил та моментів наведено в табл.
Внзначити реакції опор.
Приклад 1 .Прямокутна плита силою тяжіня Р (рис.1.), що завкріплена в точці А кульковим шарніром, у точці В — петлею й утримується в горизонтальному положенні стрижнем СЕ, знаходиться в рівновазі під дією снли F.
Визначити реакції в опорах, а також зусилля в стрижні, якщо
![]() кН
,
кН
,
![]() =
6кН ,
=
6кН ,
![]() =
1м.
=
1м.
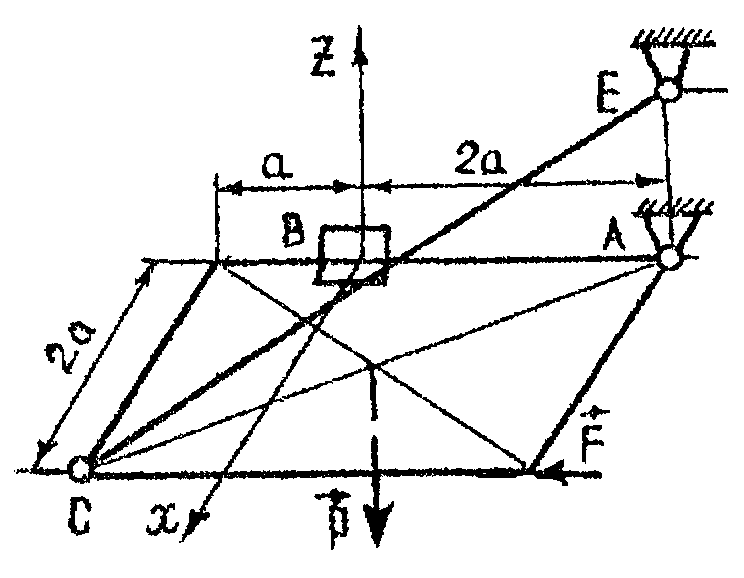 Рис.1
Рис.1
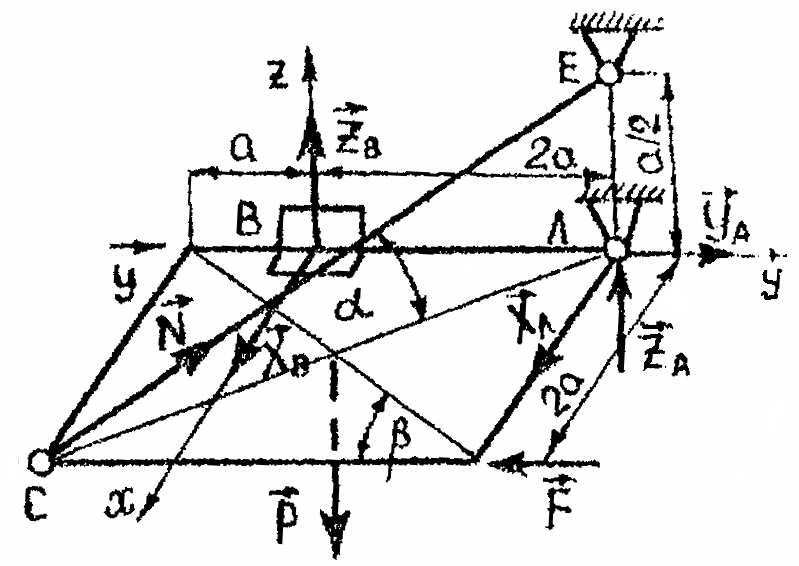 Рис.1а
Рис.1а
Розв’язання
. До об’єкта рівноваги , яким є плита
,прикладаємо активні сили
![]() та
та
![]() ,а
також реакції опор А , В і зусилля
,а
також реакції опор А , В і зусилля
![]() в
стрижні. Реакція кульового шарніра А
визначається трьома складовими
в
стрижні. Реакція кульового шарніра А
визначається трьома складовими
![]() ,
,
![]() ,
,
![]() , а петлі В – двома
, а петлі В – двома
![]() та
та
![]() (рис.1а)
(рис.1а)
Для довільної просторової системи сил записуємо шість рівнянь рівноваги у вибраній системі координат :
![]() F
F![]()
![]() =
0,
=
0,
![]() +
+![]() -
-
![]() =
0 ;
(1)
=
0 ;
(1)
![]() F
F![]() =
0,
=
0,
![]() -
-![]() +
+
![]() = 0 ;
(2)
= 0 ;
(2)
![]() F
F![]() =
0,
=
0,
![]() +
+
![]() -
-
![]() +
+
![]() =
0 (3)
=
0 (3)
![]() М
М![]() (
(
![]() )
= 0,
)
= 0,
![]()
![]() 2а
-
2а
-
![]() а
-
а
-![]()
![]() 0,5
а =
0 (4)
0,5
а =
0 (4)
![]() М
М![]() (
(
![]() )
= 0,
)
= 0,
![]()
![]() а
-
а
-
![]()
![]() 2а
= 0
(5)
2а
= 0
(5)
![]() М
М![]() (
(
![]() )
= -
)
= -
![]()
![]() 2а
+
2а
+
![]()
![]() 2а
-
2а
-
![]() а -
а -![]()
![]() 2
а =
0 (6)
2
а =
0 (6)
Тут кути
![]() і
і
![]() введено
для спрощення запису рівнянь .
введено
для спрощення запису рівнянь .
![]() =0,554
;
=0,554
;
![]() = 0,8.
= 0,8.
sin![]() =
=
![]() =
=
![]() =
0.137; cos
=
0.137; cos![]() =
=
![]() =
=
Із рівняння (5) маємо:
N =
![]() kH.
kH.
Із рівняння (4) маємо:
ZA=![]()
З рівняння (6) маємо:

Із рівняння (1) маємо:
XB=Ncos![]() cos
cos![]() _XA=7.3
_XA=7.3![]()
З рівняння (2) маємо:
YA=F_
Ncos![]() cos
cos![]() =6_7.3
=6_7.3![]()
З рівняння (3) маємо:ZB=P_Nsin![]() -
ZA=2-7,3
-
ZA=2-7,3![]() -
1
-
1
Приклад 2 . Горизонтальна прямокутна плита вагою Р закріплена сферичним
шарніром у крапці А ,циліндричним
(підшипником) у крапці В і невагомим
стержнем
![]() .На
плиту в площині , паралельній
.На
плиту в площині , паралельній
![]() ,
діє сила
,
діє сила![]() ,
а в площині рівнобіжної площині А
,
а в площині рівнобіжної площині А![]() -
пара сил з моментом М.
-
пара сил з моментом М.
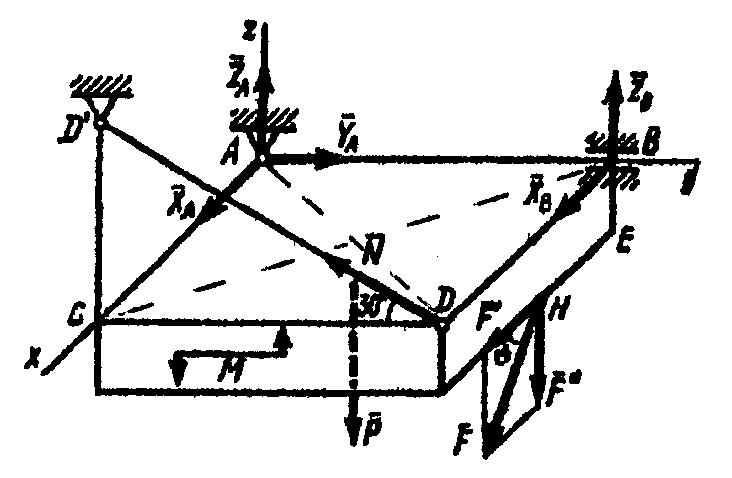 Рис.2
Рис.2
Розв”язання.1.
Розглянемо рівновагу плити .На плиту
діють задані сили
![]() ,
,![]() і
пара з моментом М, а також реакції в’язей
. Реакцію сферичного шарніра розкладаємо
на три складові
і
пара з моментом М, а також реакції в’язей
. Реакцію сферичного шарніра розкладаємо
на три складові
![]() ,
,![]() ,
,![]() ,
циліндричного (підшипника) – на дві
складові
,
циліндричного (підшипника) – на дві
складові
![]() ,
,![]() (у
площині , перпендикулярній осі підшипника
); реакцію
(у
площині , перпендикулярній осі підшипника
); реакцію
![]() стрижня
стрижня
направляємо уздовж стержня
від
![]() до
до
![]() ,
припускаючи , що він розтягнутий.
,
припускаючи , що він розтягнутий.
