15. Критерії відповідності характеристик змодельованої базової випадкової величини, та її теоретичних характеристик.

15. Перевірка на рівномірність росподілу псевдовипадкових чисел за гістограмою.

22. Перевірка якості згенерованих псевдовипадкових чисел за моментами розподілу

Для ідеального генератора псевдовипадкових чисел математичне сподівання їх дорівнює  , а дисперсія —  . Нехай маємо послідовність чисел  , здобутих за допомогою генератора псевдовипадкових чисел на ЕОМ. Для цих чисел

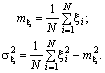
Послідовність згенеровано правильно, якщо

Для перевірки також використовують оцінку кореляційної функції

Якщо в 0 значенні вона дорівнює дисперсії, а в інших значеннях наближається до 0, то послідовність згенеровано правильно.

23. Перевірка якості згенерованих псевдовипадкових чисел на періодичність

Якщо серед множини програмно утворюваних випадкових чисел   немає однакових, а   збігається з одним із створених раніше чисел, то l називається відрізком аперіодичності. Очевидно, що 

Під час дослідження генератора випадкових чисел необхідно встановити довжину відрізка аперіодичності. Якщо число необхідних для експериментів випадкових чисел менше за довжину відрізка аперіодичності l, то датчик можна використовувати. У противному разі довжину відрізка аперіодичності слід збільшити, застосувавши різні штучні прийоми, зокрема змінивши початкове число  або використавши інший генератор.

24. Алгоритм імітаційного моделювання випадкових послідовностей з дискретними розподілами

Нехай - послідовність незалежних випадкових величин, кожна з яких має один і той же дискретний розподіл (т – скінченне число або т = ∞)

,

І нехай - послідовність незалежних випадкових величин, рівномірно розподілених у інтервалі [0,1].

Розглянемо розбиття відрізка [0,1] на т інтервалів точками s₀, .

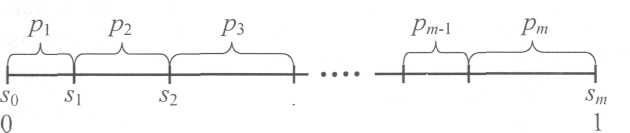
Легко бачити, що

Тобто, ймовірність попадання в к -ий інтервал рівна ймовірності того, що випадкова величина набуде значення х_t. Звідси, очевидним чином, випливає алгоритм імітаційного моделювання випадкової послідовності . А саме: для будь-якого t = 0,1 отримуємо реалізацію і шукаємо той k-ий інтервал , у який попадає , тобто , після цього маємо: . Наведений алгоритм можна представити у вигляді наступного співвідношення:

де

Звичайно, на практиці, немає потреби наперед здійснювати розбиття відрізка [0,1], а потім аналізувати кожен отриманий підінтервал (особливо, коли M = ∞). Достатньо, наприклад, скористатися цілком зрозумілим алгоритмом, блок-схему якого наведено на рис. 2.2.

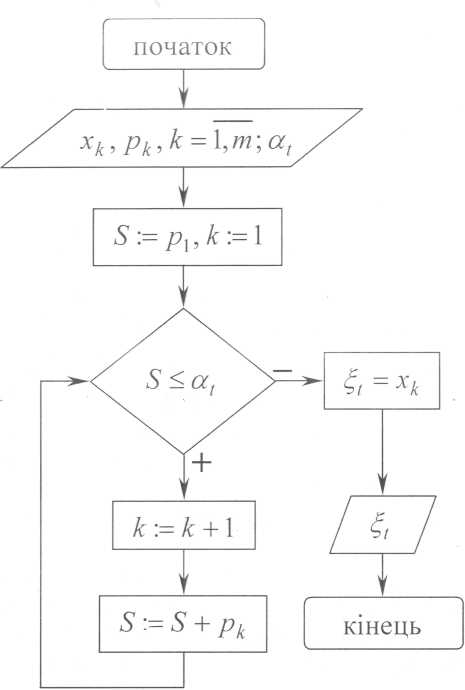
25. Імітаційне моделювання дискретної випадкової величини

Розподіл дискретної випадкової величини може бути поданий у вигляді таблиці

Xi	x1	x2	…	xn
pi	p1	p2	…	pn

Тут pj — імовірність того, що випадкова величина х набуває значення хj, j = 1, …, n.

Накладається також умова:

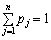
Поділимо інтервал (0; 1) на n відрізків, довжини котрих дорівнюють заданим імовірностям. Якщо випадкове число x, що формується генератором випадкових чисел, котрі відповідають рівномірному закону розподілу на інтервалі (0; 1), потрапляє до інтервалу pk, то випадкова величина х набуває значення хk. Отже, під час моделювання дискретної випадкової величини фактично використовується та сама процедура, що й за моделювання повної групи несумісних подій.