Правильность методики оценивается как удовлетворительная

0. < 0.0115981

Зависимость случайной составляющей погрешности измерений от величины среднего значения определяемой величины выражается как:

Y=0.00005152+0.010200552*X

Коэффициент корреляции равен 0.96068117

Хср1=0,005 Dn1=0.000084

Хср2=0,009 Dn2=0.0001686

Хср3=0,02 Dn3=0.0002488

Зависимость случайной составляющей погрешности измерений, проводимых с двумя параллельными определениями, от величины среднего значения определяемой величины выражается как:

Y=0.00083904+0.16525801*X

Зависимость систематической составляющей погрешности измерений, от величины среднего значения определяется аналогично.

Задача 3.4: Построить трехгодичную кривую изменения атмосферного давления и провести анализ тенденции этого изменения по данным выборки.

Скользящее среднее – это метод, позволяющий упростить анализ тенденции за счет сглаживания колебаний измерений по временным интервалам. Эти колебания могут возникать из-за случайного “шума”, который часто является побочным эффектом техники измерения. Например, измерения атмосферного давления будут зависеть и от точности барометра, и от того, насколько внимательно исследователь будет фиксировать показания прибора. Однако можно выполнить ряд измерений, затем сгладить их по отрезкам времени и построить окончательную кривую, которая будет более точно отражать фактическое значение атмосферного давления. Используется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Каждое прогнозируемое значение основано на формуле:

, где (3.4.1)

• N - число предшествующих периодов, входящих в скользящее среднее

• A_j - фактическое значение в момент времени j

• F_j - прогнозируемое значение в момент времени j

Предположим, мы создали трехгодичную кривую изменения атмосферного давления, показанную на рис. 2.4.1. Для построения менее “шумной” линии тренда для этих данных можно использовать шестимесячное скользящее среднее. Первая точка в кривой скользящего среднего – это среднее за первые шесть месяцев (Январь – Июнь 2000 года). Следующая точка – среднее со второго по седьмой месяцы (Февраль – Июль 2000 года) и т.д. Инструмент Скользящее среднее выполняет этот анализ вместо пользователя.

Таблица 3.4.1

Изменение атмосферного давления

Месяц	атм. Давление, мм рт.ст.	Скользящее среднее по 6 месяцам		Месяц	атм. Давление, мм рт.ст.	Скользящее среднее по 6 месяцам
янв.	753,4	#Н/Д		июл. 01	759,2	758,52
фев.00	758	#Н/Д		авг. 01	763,2	758,225
мар.00	745,8	#Н/Д		сен. 01	754,1	759,8333333
апр.00	753,2	#Н/Д		окт. 01	760	760,4
май.00	756,9	#Н/Д		ноя. 01	762,3	759,76
июн.00	768,5	755.9666667		дек.01	753,5	758,7166667
июл.00	754	756.0666667		янв. 02	753,9	757,8333333
авг.00	756,4	755.8		фев. 02	763,2	757,8333333
сен.00	754,3	757.2166667		мар. 02	764,6	759,5833333
окт.00	750	756.6833333		апр. 02	757,4	759,15
ноя.00	751	755.7		май. 02	753,6	757,7
дек.00	754	753.2833333		июн. 02	754,2	757,8166667
янв. 01	763,6	754.8833333		июл.02	767,9	760,15
фев.01	759,7	755.4333333		авг.02	765,6	760,55
мар.01	753,4	755.2833333		сен.02	751,5	758,3666667
апр.01	758,7	756.7333333		окт.02	756,7	758,25
май.01	761,4	758.4666667		ноя.02	753,2	758,1833333
июн.01	759,4	759.3666667		дек.02	760	759,15

На рис.3.4.2 представлено шестимесячное скользящее среднее вместе с исходной кривой изменения атмосферного давления. Инструмент Скользящее среднее возвращает выходные данные в соседний с исходными данными столбец, который и использовался для построения сглаженной кривой в диаграмме. Первые пять ячеек выходного диапазона содержат ошибочное значение #Н/Д (#N/A). Если интервал равен n, мы всегда будем иметь n-1 ошибочное значение #Н/Д в начале выходного диапазона. Включение этих значений в диаграмму не создает трудностей, так как Excel просто оставляет пустой начальную область сглаженной кривой.

Итак, сначала нам необходимо построить график изменения атмосферного давления в течение нескольких месяцев. Для этого в Excel построим таблицу, состоящую из двух столбцов: месяц и атмосферное давление, мм рт ст. Заполним соответствующие ячейки таблицы значениями, приведенными в таблице 3.4.1.

Затем для построения графика воспользуемся мастером диаграмм, расположенным на панели инструментов. С помощью четырех окон, последовательно появляющихся на экране, мастер диаграмм соберет всю необходимую для построения графика информацию.

Шаг 1: выбираем тип диаграммы – график, вид: график с маркерами, помечающими точки данных.

Шаг 2: в строке диапазон данных вводим необходимый диапазон, устанавливаем: ряды в столбцах. В закладке ряд: вводим диапазон подписи по оси Х (название месяцев).

Шаг 3: в строки название диаграммы, ось Х и ось У вводим соответствующие названия, остальные вкладки заполняем по желанию.

Шаг 4: выбираем месторасположение диаграммы: на имеющемся листе или на отдельном.

В результате мы должны получить график, представленный на рис.3.4.1.

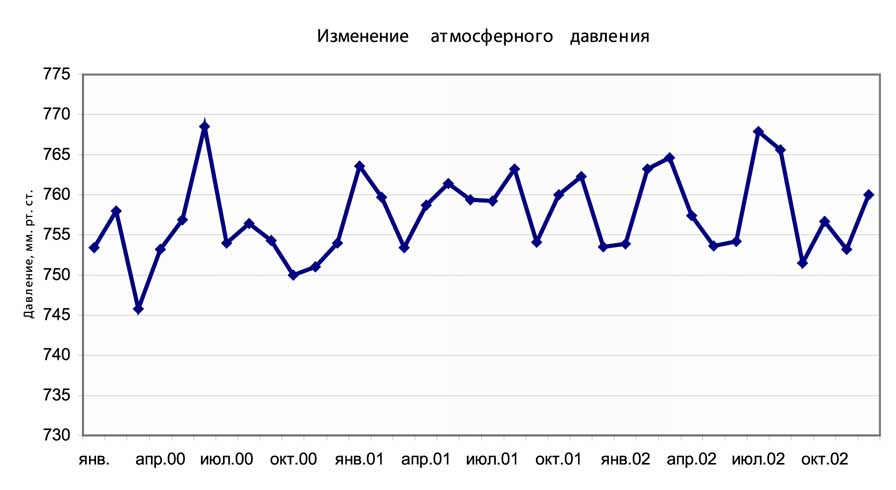
Рис.3.4.1

Следующий этап: вычисление скользящего среднего.

Для его вычисления в меню Сервис выбираем команду Анализ данных (Data analysis), затем в окне диалога Анализа данных указываем инструмент Скользящее среднее (moving average) и нажимаем кнопку ОК.

Если команда Анализа данных отсутствует в меню Сервис, выбираем в меню Сервис команду Надстройки и затем – Пакет анализа в списке надстроек, после чего нажимаем кнопку ОК. Для последних версий в Файл – Параметры – Надстройки сделайте Пакет анализа активным.

Инструмент Скользящее среднее требует задания трех параметров: диапазона, которых содержит анализируемые данные: вводим соответствующие значения давления; диапазона для вычисляемых усредненных данных: указываем диапазон ячеек, в которых будут выводиться результаты анализа и интервала усреднения: для шестимесячного скользящего среднего задаем интервал равный 6.

Ставим галочку напротив строки: вывод графика, для наглядного отображения выводимых результатов.

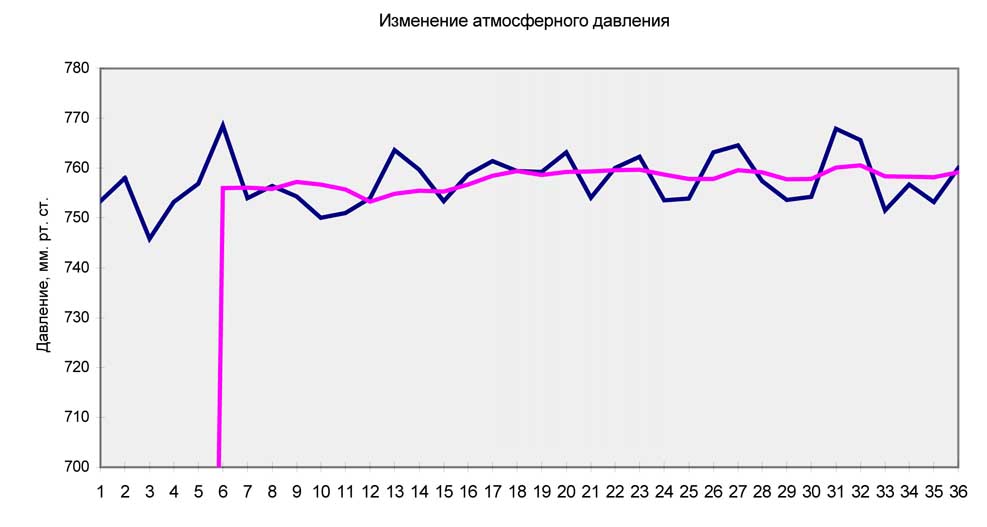
Рис.3.4.2

Как видно на экране первые несколько ячеек выводят ошибочное значение #H/Д (#N/A), причина этого была описана выше.

Кроме скользящего среднего в анализе данных предлагаются следующие инструменты анализа: одно, двухфакторный дисперсионный анализ, экспоненциальное сглаживание, анализ Фурье, корреляция, регрессия и т. д. Постарайтесь разобраться с этими инструментами самостоятельно.

Excel также представляет несколько функций для работы с линейной регрессией – ЛИНЕЙН, ТЕНДЕЦИЯ, ПРЕДСКАЗ, НАКЛОН и СТОШYX – и две – ЛГРФПРИБЛ и РОСТ – для экспоненциальной регрессии. Каждую из этих функций можно использовать с одной или несколькими независимыми переменными.

Регрессия – это статистический метод, позволяющий найти уравнение, которое наилучшим образом описывает множество данных. Регрессионный анализ основывается на сложных уравнениях и позволяет анализировать большие совокупности данных с построением соответствующих кривых зависимости. Раньше регрессионный анализ был мало доступным из-за большого объема необходимых вычислений. Но с появлением приложений для работы с электронными таблицами, таких как Microsoft Excel, которые предлагают встроенные регрессионные функции, регрессионный анализ становится все более популярным.

Линейная регрессия определяет прямую, которая наилучшим образом представляет множество данных. Основываясь на данных за текущий год, линейная регрессия поможет определить прогнозируемый подъем или спад контролируемых параметров на будущий год (изменение стока реки, изменение концентрации токсичных газов в атмосфере).

Экспоненциальная регрессия определяет экспоненциальную кривую, наилучшим образом представляющую множество данных, для которых предполагается нелинейная зависимость от времени. Например, ряд изменения роста деревьев почти всегда может быть лучше представлен экспоненциальной кривой, нежели прямой кривой.

Многомерная регрессия выполняет анализ для нескольких множеств данных; это часто дает более реалистичный прогноз. Можно проводить как линейный, так и экспоненциальный многомерный регрессионный анализ.

Функции Excel для работы с линейной регрессией так же предназначены для самостоятельного изучения.

Задача 3.5: построить математическую модель изменения температуры от концентрации СО₂ в атмосфере Земли, используя зависимости Ракиповой.

Нам известно, что в процессе хозяйственной деятельности человека ежегодно высвобождается большое количество энергии. Это происходит в основном за счет сжигания топлива и работы атомных электростанций.

Влияние энергетики на температуру атмосферы проявляется в следующем.

1. выбросы СО₂ в атмосферу от сжигания топлив приводят к увеличению количества СО₂ в атмосфере и благодаря парниковому эффекту приводят к разогреву атмосферы.

2. происходит чисто тепловой разогрев атмосферы в результате рассеяния производимой энергии.

3. сжигание топлив сопровождается загрязнением атмосферы аэрозолями. При этом меняются рассеяние, поглощение и отражение солнечной радиации в атмосфере и вследствие этого меняется температура атмосферы.

С экологической точки зрения очень важно знать, прослеживать и пытаться контролировать концентрации газов, являющихся причиной парникового эффекта.

Механизм парникового эффекта объясняется различием поглотительной способности атмосферы для приходящего к Земле излучения Солнца и излучения, уходящего от Земли. Атмосфера сравнительно хорошо пропускает идущее от Солнца коротковолновое излучение (90% энергии солнечного излучения приходится на диапазон спектра 0,4 – 4 мкм). Земля излучает полученную от Солнца энергию в длинноволновом диапазоне (участок спектра 5 – 100 мкм). В этом диапазоне происходит интенсивное поглощение излучения молекулами различных газов, что вызывает разогревание атмосферы, называемое парниковым эффектом.

Одним из таких газов является СО₂. Вид зависимости температуры от содержания СО₂ в атмосфере был определен расчетным путем многими учеными на основании различных модельных представления. Результаты расчетов расходятся не слишком сильно. Следует отметить, что изменением режима влажности и осадков, вызванным изменением температуры, либо пренебрегали, либо проведенные расчеты не позволяли сделать выводы относительно изменения режима влажности и осадков в зоне, занятой растительностью. Для наших расчетов мы использовали зависимость, полученную Л.Р. Ракиповой и О.Н.Вишняковой, в которой, как и в большинстве других работ, изменение режима влажности и осадков считалось незначительным. В результате для расчетов была получена аппроксимация зависимости в виде:

(3.5.1)

где

Т_g - отклонение средней глобальной температуры атмосферы у поверхности Земли от современного значения,

Z – относительное содержание СО₂ в атмосфере (по отношению к современному значению). В современном состоянии биосферы Т_g = 0 и Z = 1. Полученная аппроксимация достаточно точна и производная dT_g/dZ непрерывна в точке Z = 1.

Вид зависимости изображен на рис. 3.5.1. Видно, что температура есть возрастающая функция количества атмосферного СО₂. Увеличение количества СО₂ в атмосфере на 20% приводит к увеличению температуры на 0,3С. Увеличение атмосферного СО₂ вдвое приводит к увеличению температуры на 1,3С.

Итак, в ячейку А1 вводим Z, в ячейку В1 – Т. Далее в диапазон А2:А11 введем числа от 1 до 10, используя функцию Автозаполнения. После этого в ячейке В2 с помощью специальной встроенной функции ЕСЛИ создаем формулу:

=ЕСЛИ(A2>=1;2,5*(1-EXP(-0,82*(A2-1)));-5,25*A2^2+12,55*A2-7,3),

которая является электронным аналогом формулы (3.5.1), в случае Z ≥ 1, формула Excel высчитывает значение T_g по первому уравнению, в случае Z < 1 – по второму. Затем «растянем» введенную формулу для всех значений Z.

Таблица 3.5.1

Z	T
1	0
2	1,398921
3	2,01505
4	2,286413
5	2,405929
6	2,458568
7	2,481752
8	2,491963
9	2,49646
10	2,498441

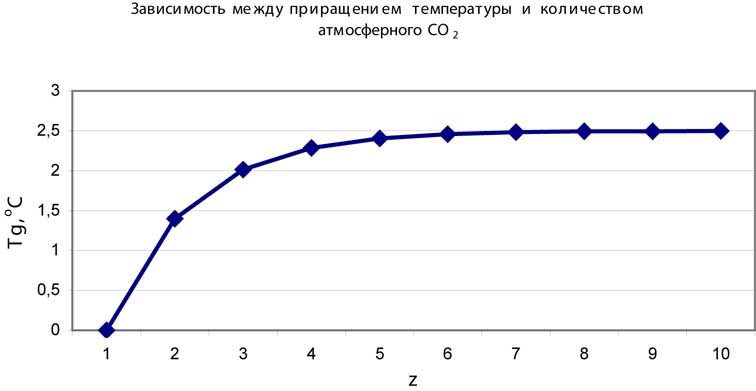
Рис.3.5.1

Использование логических функций значительно расширяют возможности применения EXCEL. До 7 функций ЕСЛИ могут быть вложены друг в друга в качестве значений аргументов значение_если_истина и значение_если_ложь. Определите для решения какой задачи была написана следующая формула =ЕСЛИ(A3<=3,"2",ЕСЛИ(A3<=6,"3",ЕСЛИ(A3<=9,"4",ЕСЛИ(A3<=12,"5")))).

Аналогичное решение: = ЕСЛИ (И(A1 >= 10, A1 <= 12), "Отлично"; ЕСЛИ (И (A1>=7; A1<=9);"Хорошо"; ЕСЛИ (И(A1>=4;A1<=6); "Удовлетворительно"; "Неудовлетворительно"))). Обратите внимание, что в синтаксис данных функций, для исключения копирования формул, внесена ошибка.

Решите задачу по определению направления ветра при заданном азимуте. С (0-22.5); СВ (22.5-67.5) и т. д.

Задача 3.6: построить математическую модель изменения концентрации СО₂ в атмосфере Земли, используя данные исследований с 1958 по 2012 года (http://scrippsco2.ucsd.edu/data/in_situ_co2/monthly_mlo.csv). С помощью полученной модели предсказать изменение концентрации данного парникового газа на ближайшее будущее (до 2017 года).

На отличную оценку решение данной задачи необходимо начать с того, что используя интернет обновите данные измерений концентраций углекислого газа. В данном примере взяты за основу измерения проводившихся в обсерватории Мауна-Лоа на Гавайских островах в 1957 – 2012 гг.. Из базы содержащей несколько тысяч измерений по годам и месяцам с помощью функций ЕСЛИ нужно выбрать годовые минимальные (октябрь) и максимальные (май) значения концентрации. С помощью функций, функций сортировки необходимо получить таблицу аналогичную таблице 3.5.2.

Для хорошей и удовлетворительной оценки решение задачи допускается начать с построения зависимости количества атмосферного СО₂ от времени. С помощью мастера диаграмм постройте график, изображенный на рис.3.5.1.

Таблица 3.5.2

Изменение концентрации атмосферного СО₂

года	Объемные части/млн	года	Объемные части/млн	года	Объемные части/млн
1958	317,5	1976	328,94	1995	363,79
1958	313,2	1977	336,75	1995	357,76
1959	318,29	1977	331,16	1996	365,41
1959	313,26	1978	338,01	1996	359,6
1960	320,03	1978	332,55	1997	366,8
1960	313,83	1979	339,47	1997	360,77
1961	320,58	1979	333,86	1998	369,3
1961	315,38	1980	341,46	1998	364,23
1962	321,01	1980	336,02	1999	371
1962	315,42	1981	342,91	1999	365,13
1963	322,25	1981	336,86	2000	371,82
1963	315,99	1982	344,14	2000	366,73
1964	322,25	1982	337,86	2001	374,02
1964	316,79	1983	345,75	2001	368,1
1965	322,16	1983	339,99	2002	375,55
1965	317,3	1984	347,43	2002	370,25
1966	324,01	1984	341,35	2003	378,35
1966	318,1	1985	348,93	2003	373
1967	325	1985	342,8	2004	380,61
1967	319,31	1986	350,21	2004	374,22
1968	325,57	1986	344,17	2005	382,24
1968	320,25	1987	351,84	2005	376,79
1969	327,34	1987	346,36	2006	384,94
1969	321,78	1988	354,22	2006	379,05
1970	328,07	1988	348,88	2007	386,43
1970	323,16	1989	355,67	2007	380,88
1971	328,92	1989	349,99	2008	388,49
1971	323,57	1990	357,16	2008	382,81
1972	330,07	1990	351,18	2009	390,18
1972	325,06	1991	359,34	2009	384,34
1973	332,48	1991	352,21	2010	393,22
1973	327,18	1992	359,66	2010	387,15
1974	333,09	1992	353,31	2011	394,34
1974	327,37	1993	360,28	2011	388,92
1975	333,97	1993	353,99	2012	396,79
1975	328,34	1994	361,68
1976	334,87	1994	355,99

Анализируем график: видны уменьшения концентрации СО₂ летом и повышением концентрации СО₂ зимой, что объясняется сезонным развитием наземной растительности в Северном полушарии. В целом за данный период рост СО₂ составил 0,28% в год. Аналогичный рост концентрации атмосферного СО₂ наблюдается во всех обсерваториях. Это говорит о том, что ожидаемый в ближайшие годы рост концентрации атмосферного СО₂ будет достаточно велик, что может привести к заметному изменению температуры атмосферы.

Зависимость, рассмотренная нами, была построена в начале 80-х годов. Т.о. мы можем проследить изменение концентрации СО₂ в воздухе до наших дней и сделать прогноз на ближайшее будущее. Это возможно сделать с помощью такой функции, как линия тренда. Линия Тренда – это линия регрессии, которая аппроксимирует точки данных, или линия скользящего среднего. Линии тренда графически иллюстрируют тренд (тенденцию изменения) рядов данных. Линии тренда обычно используются, когда необходимо решить задачи прогнозирования и экстраполяции (т. е. задачи регрессионного анализа, когда одна переменная может быть представлена через другие). С помощью регрессионного анализа можно продолжить линию тренда вперед или назад, экстраполировать ее за пределы, в которых данные уже неизвестны и показать их тренд - тенденцию изменения. Можно также построить скользящее среднее, которое сглаживает случайные отклонения.

Для создания линии тренда необходимо выполнить следующие действия: наводим курсор на график и нажимаем правую кнопку мыши, появляется контекстное меню, в котором выбираем команду: добавить линию тренда.

Для данного ряда данных приемлемо выбрать 3-ий тип линии тренда – полиномиальную линию тренда 3-ей степени. В закладке Параметры указываем прогноз на необходимое число периодов вперед, ставим галочку напротив строк: показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Затем нажимаем кнопку ОК. Результат видим на экране (рис.3.5.3).

Как видно из графика, наблюдается постепенное повышение концентрации СО₂ в воздухе в данный период времени. Задав параметры линии тренда – прогноз вперед на n периодов, возможно проследить изменение концентрации СО₂ в воздухе, но необходимо учитывать тот факт, что значения будут не точными, а приближенными, т.к. значение остаточного квадратного отклонения (R²)=0,98038384. Уравнение линии тренда имеет вид: y=-0,00000679x³+0,00423210x²+0,34009010x+314,50813027

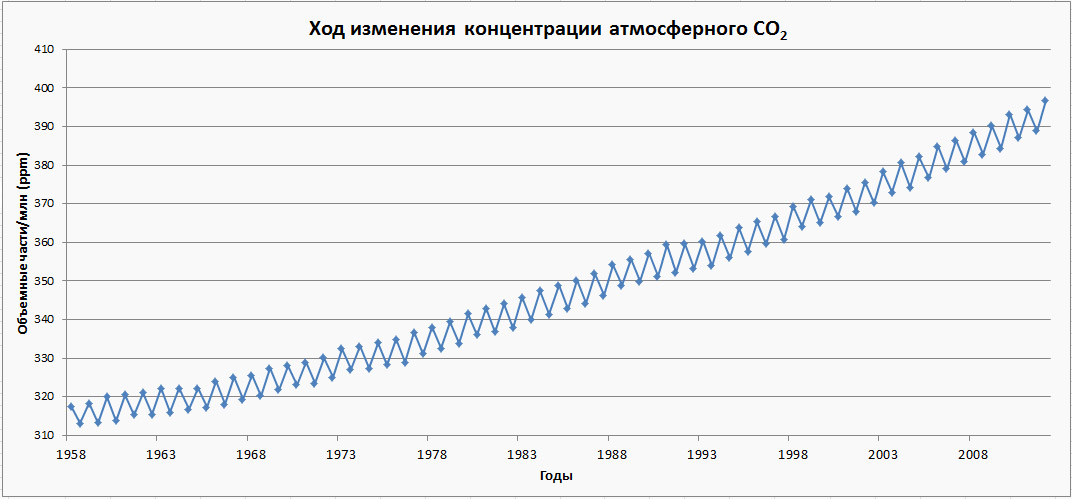Рис.3.5.2

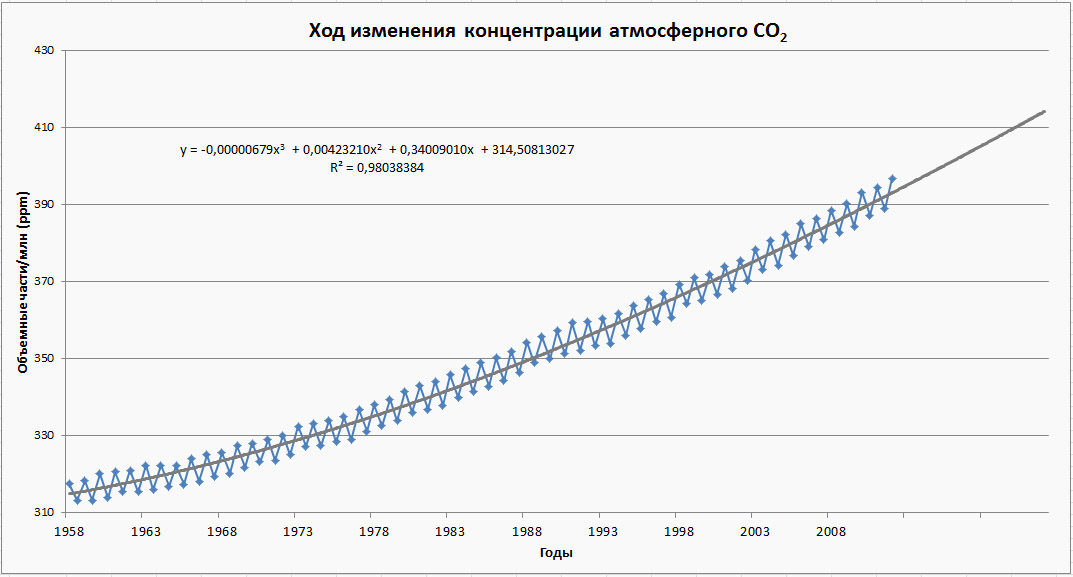
Рис.3.5.3

Инструменты Excel делают возможным проследить изменения концентрации СО₂ в атмосфере до наших дней, а также предсказать возможное количество парникового газа в атмосфере будущего.

Выделив курсором мышки линию тренда и нажав правую кнопку мыши, в появившемся окне выбираем команду Формат линии тренда. И осуществляем необходимые нам изменения. В данном конкретном случае нам следует лишь увеличить количество прогнозируемых периодов (например, на 10 или 20), для того, чтобы иметь представление о предполагаемом по данной математической модели увеличении концентрации СО₂ в настоящий период времени и в ближайшем будущем. Постройте график аналогичный рис 3.5.3.

С использованием линии тренда можно решать простейшие задач прогнозирования с использованием различных функций интерполяции: логарифмической, экспоненциальной, полиномиальной, степенной и т. д. Для этого на панели Тип выберите нужный тип регрессионного анализа (экстраполяции) линии тренда или тип “скользящей средней”.

Задача 3.7: построить кривую изменения численности населения Земли. Аппроксимировать полученную кривую с помощью экспоненциальной и степенной функции.

год	Население, т.ч.		год	Население, т.ч.		год	Население, т.ч.
-4000	7		1300	360		1950	2418,6
-1000	50		1340	443		1955	2755,8
-500	100		1400	350		1960	3021,4
0	170		1500	425		1965	3334,8
200	190		1600	545		1970	3692,9
400	190		1650	470		1975	4068,1
500	190		1700	600		1980	4434,6
600	200		1750	791		1985	4830,9
700	210		1800	978		1990	5263,5
800	220		1850	1262		1995	5674,3
900	226		1900	1650		2000	6070,6
1000	310		1910	1750		2005	6343,6
1100	301		1920	1860		2010	6900
1200	360		1930	2070
1250	400		1940	2300

Решение данной задачи с использованием линии тренда не позволяет получить оптимальный результат. Поставленная задача нагляднее всего решается путём ручного подбора коэффициентов экспоненциальной или степенной зависимости.

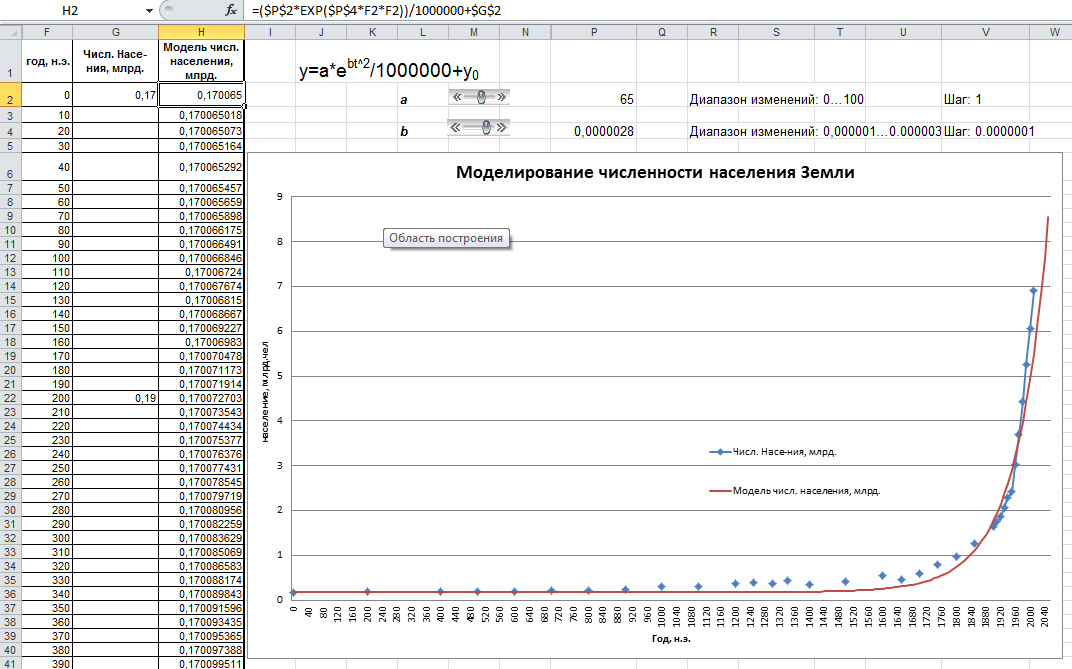
Задача 3.8: рассчитать зону поражения отравляющим веществом при заданной постоянной скорости ветра и известному времени продолжительности аварии.

Решением данной задачи будет круговая диаграмма построенная на рисунке

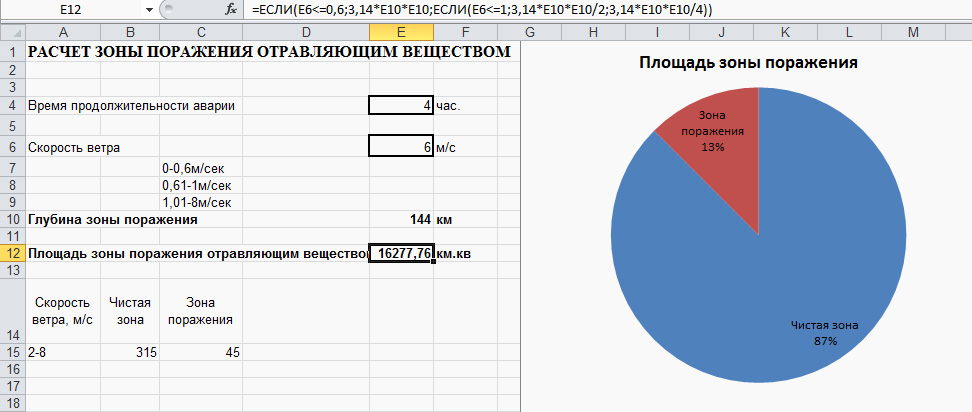
Рис.3.7.1

Обратите внимание, что расчёт площади поражения используются три разные формулы в зависимости от скорости ветра.

Если скорость ветра от 0 до 0,6, то- «=3,14*Е10²»

Если скорость ветра от 0,61 до 1, то- «=3,14*Е10²/2»

Если скорость ветра от 1,01 до 8, то- «=3,14*Е10²/4»

Расчёт глубины зоны поражения осуществляется по формуле «=Е4*Е6*6»

Чистая зона и зона поражения, ячейки В15 и С15 задаются формулами: =ЕСЛИ(E6<=0,6;360;ЕСЛИ(E6<=1;180;ЕСЛИ(E6<=2;270;315)))

Контрольные вопросы:

1. Что такое линия тренда?

2. Как можно использовать команду Подбор параметров?

3. Что такое консолидация данных?

4. Что включают в себя метрологические характеристики?

5. Что такое аппроксимация функции?

6. Какие функции для работы с линейной регрессией Вы знаете?

7. Что такое Скользящее среднее?

8. Каким способом возможно предсказать изменения некоторых величин во времени?