Контрольные вопросы

1. Что представляет собой внедренная диаграмма и в каком случае она применяется?

2. Какие типы диаграмм можно построить с помощью Excel?

3. Перечислите основные шаги построения диаграмм.

4. Как перенести внедренную диаграмму в лист диаграмм и диаграмму из листа диаграмм внедрить в рабочий лист?

5. Как вставить пустой лист диаграмм?

6. Как удалить данные из диаграммы и как вносить новые данные?

7. Какими способами можно вставить название и легенду диаграммы?

8. Как записывается свободно позиционируемый текст в диаграмме?

9. Как изменить данные непосредственно на диаграмме или графике? Отражаются ли эти изменения на других диаграммах и данных?

10. Что такое Мастер текстов и его применение?

11. Перечислите способы с помощью которых данные из текстовых файлов можно поместить в Excel.

12. Чем отличается абсолютная ссылка от относительной?

Практическая работа № 3 Использование Excel в математическом моделировании и прогнозировании состояния окружающей среды

Цель работы: изучить возможности Excel в решении экологических задач

Теоретическая часть

Научно-технический прогресс, и прежде всего, быстрый рост энергетической мощности цивилизации порождает многочисленные проблемы, требующие глубокого научного анализа. Они вызваны прежде всего масштабом прямого воздействия человеческой деятельности на окружающую среду. Вырубка лесов, замена естественных ценозов искусственными, эрозия почв, различные загрязнения и многое другое изменяют, деформируют установившийся ход природных процессов и, следовательно, меняют условия жизни и деятельности людей.

Важную роль здесь будут играть создание и анализ математических моделей, описывающих протекающие в биосфере динамические процессы, при этом особое значение приобретает машинная имитация изучаемых процессов, математическое моделирование, является сплавом математических методов и конкретных естественно-научных исследований. Предмет математического моделирования систем, как науки, составляют экологические процессы и системы, а методом исследования этой науки является математическое моделирование, т.е. построение математических моделей и анализ их подходящими средствами современной математики.

В экологии математические модели – это не цель, а лишь средство изучения реальных систем. Поэтому возникает вопрос о возможностях и границах применимости ММСОС при решении конкретных задач прикладной и теоретической экологии. Среди этих задач – прогнозирование поведения экосистем под действием тех или иных антропогенных факторов, выбор оптимальной стратегии эксплуатации экосистемы, управление популяциями и сообществами, экологическая оценка различных технологий сельского хозяйства и т.д.

Реальные явления, с которыми человек сталкивается на практике, настолько сложны, что при их анализе приходится отвлекаться от ряда несущественных второстепенных признаков и создавать новый, порой идеальный образ, в котором учтены существенные стороны явления. Этот образ, имитирующий реальный объект называется его моделью.

Существует огромное количество специальных программ, которые созданы для построения математических моделей в разных областях науки, в частности такие программы существуют и для изучения процессов, происходящих в биосфере.

Например, Mathcad - программное средство, среда для выполнения на компьютере разнообразных математических и технических расчетов, снабженная простым в освоении и в работе графическим интерфейсом, которая предоставляет пользователю инструменты для работы с формулами, числами, графиками и текстами. В среде Mathcad доступны более сотни операторов и логических функций, предназначенных для численного и символьного решения математических задач различной сложности. Отличительной чертой Mathcad являются так называемые документы, которые объединяют описание математического алгоритма решения задачи (или ряда задач) с текстовыми комментариями и результатами вычислений, заданными в форме символов, чисел, таблиц или графиков. Более детальным изучением этой программы, построением динамических экологических моделей в среде Mathcad мы займёмся на следующем курсе, при изучении дисциплины Математическое моделирование экологических систем и технологий.

В настоящее время самой распространённой математической программой, установленной практически на всех компьютерах является Microsoft Excel – программа входящая в состав Microsoft Office. Excel сочетает в себе очень простой и удобный интерфейс, распространённость и в тоже время эта программа позволяет решать и анализировать широкий спектр задач экологии.

Программу Excel можно настраивать в соответствии с индивидуальными запросами очень широкого круга пользователей. Каждый пользователь программы Excel, определив круг наиболее часто используемых функций, может организовать работу с ними наиболее удобным для себя образом. С другой стороны, те функции программы, которые никогда не используются, можно вообще убрать из конфигурации, чтобы сэкономить ресурсы компьютера и повысить эффективность обработки. С учётом того, что у Вас уже есть достаточный опыт работ в Excel предлагается начать данную лабораторную работу с создания наиболее удобного интерфейса, необходимого для решения задач. Вы имеете возможность создать собственные панели инструментов, составляя их более чем из пятисот готовых кнопок, палитр и полей со списками или используя кнопки, разработанные лично вами. При первом запуске Microsoft Excel на экране появляются две панели инструментов: Стандартная и Форматирование, однако Excel имеет еще множество других панелей инструментов, на которые можно поместить огромное количество дополнительных кнопок.

Рис. 3.1

Вы можете разместить панели инструментов Стандартная и Форматирование на отдельных строках. Для этого в меню Сервис выберите команду Настройка и затем на вкладке Параметры открывшегося окна диалога снимите флажок Стандартная панель и панель форматирования в одной строке.

Для того чтобы скрытые кнопки были видимы, достаточно щелкнуть на стрелке вниз в правом конце панели инструментов, чтобы открыть меню Другие кнопки. Здесь Вашему вниманию предлагается обширный набор кнопок, которые можно вывести на видимую часть панели инструментов, поставив флажок напротив необходимой кнопки.

В любое время Вы можете вывести на экран сколько угодно дополнительных панелей инструментов, как показано на рис. 3.2. Правда, при этом возможно придется пожертвовать размерами окна листа. Для активизации панели инструментов выберите в меню Вид команду Панели инструментов и затем укажите нужную панель инструментов в подчиненном меню.

Рис. 3.2

Удалить панель инструментов не сложно. Достаточно, открыв контекстное меню панелей инструментов, убрать флажок рядом с ее именем.

В Excel кроме кнопок и команд, которые уже включены во встроенные панели инструментов и строки меню, имеется значительное число дополнительных кнопок и команд.

Вы можете также создать собственную панель инструментов очень просто, выполнив следующие действия:

1. В меню Вид выберите команду Панели инструментов, а затем – Настройка.

2. На вкладке Панели инструментов нажмите кнопку Создать.

3. После этого появится окно диалога Создание панели инструментов. Введите имя для новой панели инструментов. Нажмите Ok, и на экране появится небольшая, пустая и незакрепленная панель инструментов.

4. Добавьте в новую панель нужные кнопки, перетаскивая их с вкладки Команды окна диалога Настройка или копируя с других панелей инструментов.

После определения новой панели инструментов и закрытия окна диалога Настройка ее имя появится в подменю Панели инструментов, в контекстном меню и в списке на вкладке Панели инструментов окна диалога Настройка. Пользовательскую панель инструментов можно вывести на экран, скрыть и закрепить, как любую встроенную панель инструментов Excel.

После того, как Вы разобрались с настройкой панелей инструментов Excel, оставьте только стандартную и форматирования и переходите к решению задач. При использовании последних версий зайдите в меню Файл – Параметры – Настройка ленты.

Задача 3.1: проведенные замеры показали, что в воздухе присутствуют такие вещества, как ацетон и аммиак NH₃, с концентрацией 190 и 55 мг/м³ соответственно. Вещества обладают аддитивным действием, ПДК ацетона – 200 мг/м³, аммиака – 20 мг/м³. С помощью Excel определить возможную концентрацию аммиака.

Данную задачу решим с помощью команды Подбор параметра.

Введем данные в ячейки Excel А1:A5 и B1:В4:

рис. 3.1.1

В ячейку В5 введем формулу, являющуюся условием безопасного действия данной смеси газов, ссылаясь на ячейки, содержащие необходимые данные:

(3.1.1)

В электронном виде эта формула будет иметь вид: =В1/В3+В2/В4, где

В1 – ячейка, содержащая значение концентрации ацетона;

В3 – ячейка, содержащая значение ПДК ацетона;

В2 – ячейка, содержащая значение концентрации аммиака;

В4 – ячейка, содержащая значение ПДК аммиака.

Для введения формулы активизируем ячейку В5, ставим знак “=”, которые соответствует началу записи формулы, затем, оставляя ячейку В5 активной, щелкаем с помощью курсора мышки на ячейку В1, далее в строке формул видим ссылку на эту ячейку, продолжаем запись: ставим знак “/” и ссылаемся на ячейку В2, далее продолжаем запись согласно формуле. По завершению записи нажмите Enter. В ячейке В5 появляется результат вычисления.

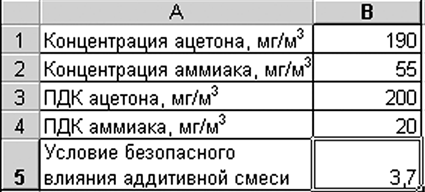
рис.3.1.2

Как видно из выражения (3.1.1), смесь будет являться безопасной, если сумма отношений концентраций к ПДК будет меньше либо равна 1, в нашем случае она равна 3,7, т.е. условие не выполняется. Следовательно, нам необходимо найти такое значение концентрации аммиака, при котором смесь не будет оказывать вредного влияния на человека.

Для этого, используя команду Подбор параметра меню Сервис, необходимо выполнить следующие действия:

1. Выделите ячейку с формулой, в данном случае В5.

2. В меню Сервис выберите команду Подбор параметра.

3. В окне диалога Подбор параметра, показанном на рис.3.1.3, оставьте без изменений значение в поле Установить в ячейке (там должна содержаться абсолютная ссылка на активную ячейку).

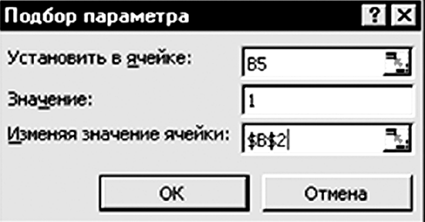
рис.3.1.3

4. В поле Значение введите максимальное значение, которое вы хотите получить в качестве результата формулы, в данном случае 1.

5. В поле Изменяя значение ячейки введите ссылку или щелкните в листе на ячейке, значение которой является неизвестным. В данном случае это ячейка В2.

6. Нажмите кнопку Ok или клавишу Enter. Excel выведет окно диалога Результат подбора параметра, показанное на рис. 2.1.4. Ответ на ваш вопрос находится в ячейке, заданной ранее в поле Изменяя значение ячейки. В данном примере результат 1 появляется в ячейке В2, т.е. для выполнения условия задачи, необходимо, чтобы концентрация NH₃ была равна 1 мг/м³.

7. Чтобы сохранить это значение, нажмите кнопку Ok в окне диалога Результат подбора параметра. Для восстановления значения, которое было в ячейке В2 до использования команды Подбор параметра, нажмите кнопку Отмена.

рис. 2.1.4

При подборе параметра Excel использует итерационный процесс. Для изменяемой ячейки, заданной в поле Изменяя значение ячейки, программа проверяет одно значение за другим, пока не получит нужное решение. В той задаче, которую мы только что рассматривали, решение может быть получено очень быстро. Другие задачи потребуют большего времени, а для некоторых решений не будет найдено вовсе.

Для последних версий EXCEL: Данные – Анализ что Если.

Задача 3.2: Тремя станциями мониторинга окружающей среды было проведено слежение за состоянием реки Днепр, пробы воды брались в течении полугода один раз в месяц, данные каждой станции приведены на отдельных листах Книги Excel. Консолидируйте данные.

Результаты измерений:

Станция 1:

	Результаты анализа проб воды реки Днепр
	Взвешенные вещества	Хлориды	Сульфаты	БПК5, мг О2 /л	Фосфаты
Январь	25	270	456	3,9	0,009
Февраль	30	327	487	4,3	0,0043
Март	28	201	390	2,5	0,0027
Апрель	21	280	509	6,5	0,0059
Май	39	387	476	4,2	0,0045
Июнь	45	359	387	4,3	0,0029

Станция 2:

	Результаты анализа проб воды реки Днепр
	Взвешенные вещества	Хлориды	Сульфаты	БПК5, мг О2 /л	Фосфаты
Январь	30	260	467	4	0,0089
Февраль	32	350	486	4,5	0,0035
Март	24	198	456	2,7	0,003
Апрель	26	300	498	6,4	0,0056
Май	39	459	587	4,7	0,0042
Июнь	44	337	432	3,4	0,003

Станция 3:

	Результаты анализа проб воды реки Днепр
	Взвешенные вещества	Хлориды	Сульфаты	БПК5, мг О2 /л	Фосфаты
Январь	27	267	578	3,6	0,0091
Февраль	35	300	483	4,2	0,0038
Март	23	200	364	2,1	0,0029
Апрель	18	349	516	6,8	0,0054
Май	43	432	432	4,5	0,0043
Июнь	40	333	386	3,9	0,0028

Введем данные в ячейки Excel. Значение замеров каждой станции будут находится на разных листах.

Так как названия строк и столбцов, а также названия самих таблиц идентичны проведем следующую операцию: находясь на Листе 1, зажмите клавишу Shift и не отжимая ее курсором выделите Лист 2 и 3, таким образом Вы сделали активными сразу три листа. Теперь все данные, записанные на Листе 1, будут автоматически копироваться на Лист 2 и Лист 3.

Введем название таблицы, названия столбцов и с помощью функции автозаполнения названия месяцев. Данные по каждой станции введем отдельно.

С помощью команды Консолидация в меню Данные мы сможем собрать все данные, находящиеся на трех листах воедино.

Консолидировать данные можно по расположению или по категориям. Если Вы консолидируете данные по расположению, Excel собирает информацию из одинаково расположенных ячеек всех исходных листов. При консолидации данных по категории Excel использует в качестве основы для объединения листов заголовки столбцов или строк. Консолидация по категории представляет большую свободу для организации данных в исходных листах.

Так как наши таблицы находятся в ячейках с одинаковыми адресами, мы можем использоваться консолидацию по расположению.

Нам необходимо создать лист Усреднение данных, для этого выполним следующие действия:

1. Создайте итоговый лист и активизируйте его. Выделите конечную область, то есть блок ячеек, в который будут помещены консолидированные данные. На рис. 2.2.1 конечная область – это диапазон В3:F8 в листе Усреднение.

2. В меню Данные выберете команду Консолидация.

3. Для усреднения значений из всех исходных листов выберите функцию Среднее в раскрывающемся списке Функция в окне диалога Консолидация. Оставьте флажки в области Использовать в качестве имен не установленными. Поскольку мы не собираемся создавать связи с исходными листами, также не устанавливайте флажок Создавать связи с исходными данными.

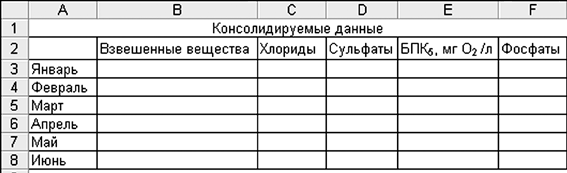
Рис.3.2.1

4. Введите ссылку для каждого исходного диапазона в поле Ссылка или выделите эти диапазоны с помощью мыши.

5. Нажмите кнопку Добавить в окне диалога Консолидация. Excel перенесет ссылку из поля Ссылка в список Список диапазона. На рис. 3.2.2 показан окончательный вид этого окна диалога.

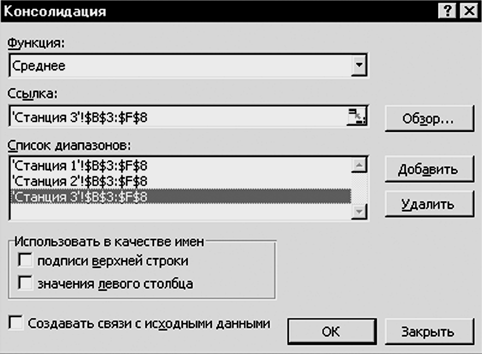
Рис.3.2.2

Нажмите кнопку Ok. Excel усреднит исходные значения и поместит их в итоговый лист, представленный на рис.3.2.3

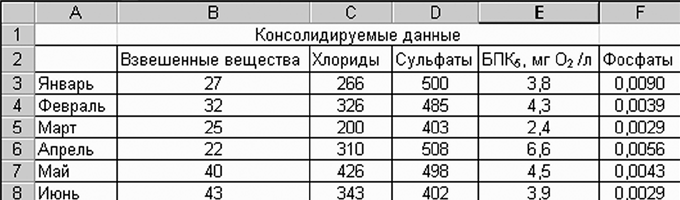
Рис.3.2.3

Задача 3.3. В биоматериале определяли массовую долю хлорорганического пестицида ДДТ. Для этого ДДТ выделяли из материала посредством экстракции гексаном с последующей очисткой экстракта концентрированной серной кислотой, и анализировали методом капиллярной газо-жидкостной хроматографии с детектором по захвату электронов. Правильность методики оценивали путем введения ДДТ в биоматериал и анализом проб с добавками ДДТ. Вычислить метрологические характеристики метода.

Исходные данные для вычисления приведены в таблице 3.3.1:

Таблица 3.3.1

Выборка №1	Выборка №2	Выборка №3
0,004337	0,007612	0,0166090
0,004236	0,007474	0,0170130
0,003943	0,007813	0,0158290
0,004253	0,008258	0,0167240
0,00396	0,007755	0,0158540
0,004048	0,007907	0,0161140
0,004004	0,007831	0,0159840
0,00429	0,008323	0,0168340
0,004343	0,008415	0,0169900
0,004263	0,008276	0,0167540
0,004341	0,008411	0,0169840
0,003991	0,007809	0,0159470
0,004081	0,007964	0,0162120
0,004304	0,008348	0,0168760
0,0041	0,007997	0,0162690

Для определения содержания загрязняющих веществ в воде используют различные методы анализа, подвергшиеся метрологической аттестации. В основе метрологической аттестации метода лежит определение его метрологических характеристик путем математической обработки результатов опытов, определения погрешностей анализа, полученных при помощи этого метода. Данный анализ более подробно рассмотрен в методических указаниях по определению метрологических характеристик методик определения загрязнителей в объектах окружающей среды. Ниже приведен только пример выполнения данных расчётов с использованием табличного процессора Excel.

Порядок проведения расчета.

1. В ячейку А1 введите «Выборка».

2. В ячейку А2 внесите N.

3. В ячейку А3 – число 1, а затем, используя автозаполнение внесите числа до 15.

4. В ячейку В2 внесите Х, а в ячейки В3-В17 – Ваши исходные данные.

5. В ячейку А19 введите слова «Математическое ожидание».

6. В ячейке В19 вычислите среднее значение исходных данных с помощью Мастера функций.

7. В ячейку С3 введите формулу =$B$19-B3. Вспомните про абсолютные и относительные ссылки (F4). После этого скопируйте формулу в ячейки С4-С17.

8. В ячейке D3 вычислите (Хср – Х)² и аналогично предыдущему значению вычислите все (Хср –Х) во второй степени.

9. В ячейку А20 внесите «Среднее квадратическое отклонение», а в ячейке В20 вычислите среднее квадратическое отклонение по формуле:

Кроме того, формулы и методика вычислений указаны в Методических указаниях по определению метрологических характеристик методик определения загрязнителей в объектах окружающей среды.

10. В ячейки А21 и В21 внесите «Действительное значение измеряемой величины» и его значение соответственно.

11. Далее необходимо проверить результаты опытов на наличие грубых ошибок. Для этого:

• вычислить значение

для чего среди исходных данных (используя мастер функций) следует выбрать максимальное и минимальное значения и поочередно подставлять их в формулу, при этом S - среднее квадратическое отклонение.

В таблице 3.3.2 указаны теоретические значение квантиля распределения t_т

Таблица 3.3.2

n	tт	n	tт
3	1.41	11	2.34
4	1.69	12	2.39
5	1.87	13	2.43
6	2.00	14	2.46
7	2.09	15	2.49
8	2.17	16	2.52
9	2.24	17	2.55
10	2.29	18	2.58

• Сравнить вычисленное значение t_max и t_т. Если t_max > t_т, то результат следует отбросить как анормальный.

• Пересчитать значения Хср и S для новой выборки.

12. В

    

    ячейках А22 – С22 вычислить границы доверительного интервала. Для чего следует в ячейке А22 вычислить левую часть неравенства, в ячейку В22 ввести < μ <, а в ячейке С22 произвести вычисление правой части неравенства.

где t_s – это квантиль распределения Стьюдента, указанный в таблице 3.3.3

n	ts	n	ts
2	12.7	11	2.23
3	4.30	12	2.20
4	3.18	13	2.18
5	2.78	14	2.16
6	2.57	15	2.14
7	2.45	16	2.13
8	2.36	17	2.12
9	2.31	18	2.11
10	2.26	19	2.10

13. Если соблюдается неравенство Xcp -  > X, (где X – это средняя поправка (см. пункт 17)), то систематическая составляющая погрешности значима и необходимо вычислить и исключить ее.

14. Для устранения погрешности необходимо найти поправку на систематическую составляющую погрешности. В ячейку А23 внесите «Поправки».

15. В ячейках А24-А39 вычислить поправку по формуле  – Хі , где  – действительное значение величины.

16. Вычислить среднюю поправку в ячейке А40 аналогично тому, как мы определяли среднее значение Х (это и будет систематическая составляющая погрешности).

17. В ячейку А41 вводим «Исправленные результаты измерений».

18. В ячейку А42 вводим N, а в ячейки А43 –А58 числа от 1 до 15.

19. В ячейку В42 вводим Х, а в ячейки В43-В58 исправленные значения Х=Хі+поправка.

20. Выполнить аналогичные операции для выборок №2 и №3.

21. В

    

    ячейку А61 вводим «Случайная составляющая погрешности измерений», а в ячейке В61 вычисляем ее по формуле:

22. В ячейку А62 – «Случайная составляющая погрешности измерений, проводимых с двумя параллельными определениями», а в ячейке В62 вычисляем ее по той же формуле, только n=2.

23. В ячейку А63 – «Воспроизводимость результатов анализа», а в ячейке В64 вычисляем Хср/S. В ячейку А65 вводим «Отношение среднего квадратического отклонения к среднему», а в ячейке В65 вычисляем его по формуле S/Xcp. В ячейку А66 вносим «Относительная погрешность», в В66 вычисляем ее как 100*Δx/μ.

24. В ячейку А67 вводим «Предел обнаружения метода», в В67 вычисляем его как S*3.

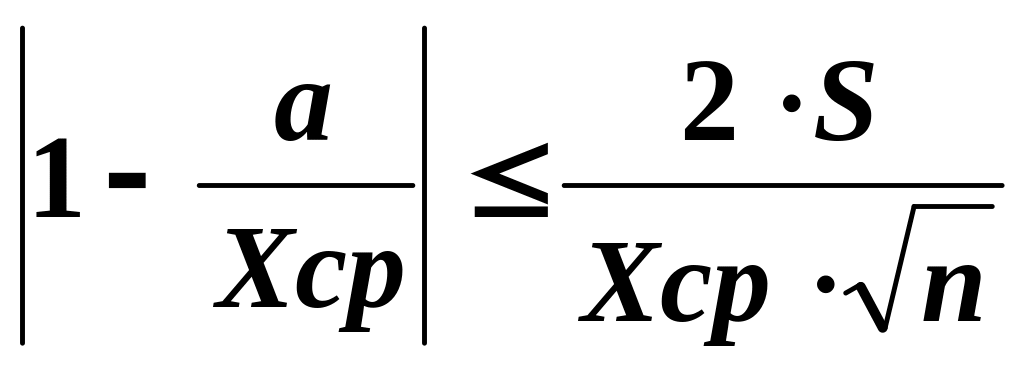25. О цениваем правильность методики, вычисляя неравенство:

где а – аттестованное значение содержания определяемого компонента в стандартном образце или известное содержание добавки (действительное значение).

В ячейке А68 вычисляем левую часть формулы, в В68 вводим знак неравенства, а в С68 вычисляем правую часть неравенства.

Если это неравенство соблюдается, то правильность методики оценивается как удовлетворительная.

После выполнения всех трех домашних заданий необходимо вычислить зависимость и коэффициенты корреляции этих зависимостей.

26. Находим зависимости между средним значением и случайной составляющей погрешности. Для этого:

• Вычисляем сумму действительных значений трех исходных данных (Σx_i).

• Вычисляем сумму случайных составляющих погрешности этих выборок (Σy).

• Вычисляем сумму произведений соответствующих друг другу действительных значений и случайных составляющих погрешности (Σxy).

• Возводим в квадрат сумму действительных значений трех исходных данных ((Σx)²).

• Вычисляем сумму квадратов действительных значений (Σx²).

• В ычисляем коэффициент В по формуле:

• В ычисляем коэффициент А по формуле:

• Вычисляем коэффициент корреляции r с помощью Мастера функций

, где

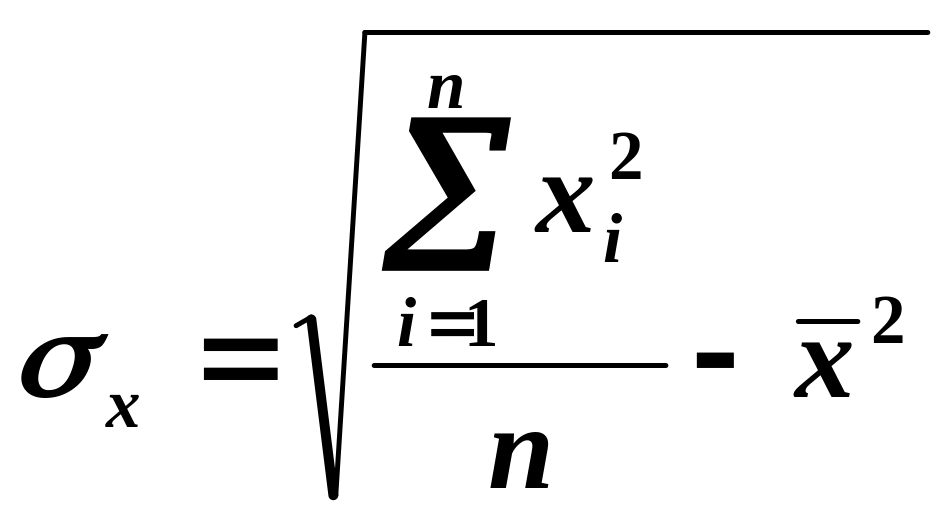
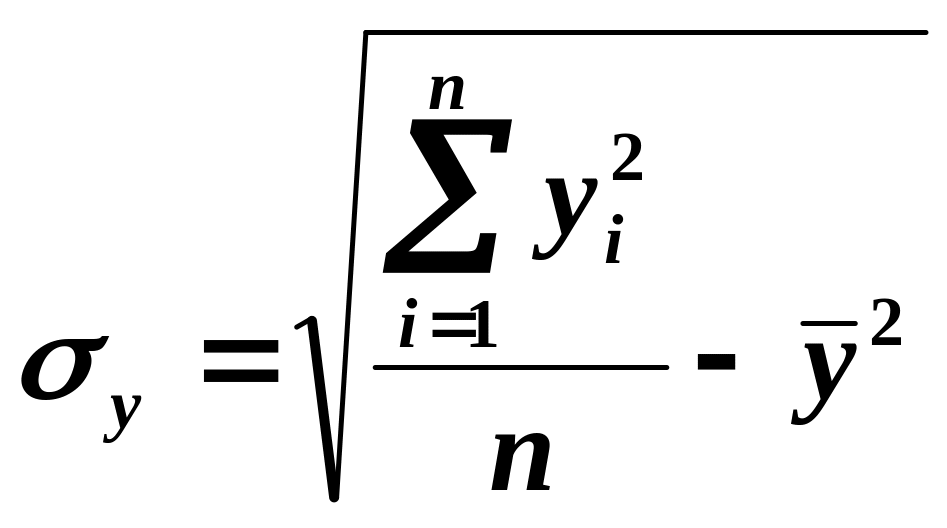
Результатом выполненной работы являются следующие таблицы и расчёты:

Исходные данные №1.

Выборка:

N	X	Хср – Х	(Хср - Х)2
1	0,004337	-0,0001707	0,0000000291
2	0,004236	-0,0000697	0,0000000049
3	0,003943	0,0002233	0,0000000498
4	0,004253	-0,0000867	0,0000000075
5	0,00396	0,0002063	0,0000000425
6	0,004048	0,0001183	0,0000000140
7	0,004004	0,0001623	0,0000000263
8	0,00429	-0,0001237	0,0000000153
9	0,004343	-0,0001767	0,0000000312
10	0,004263	-0,0000967	0,0000000094
11	0,004341	-0,0001747	0,0000000305
12	0,003991	0,0001753	0,0000000307
13	0,004081	0,0000853	0,0000000073
14	0,004304	-0,0001377	0,0000000190
15	0,004100	0,0000663	0,0000000044

Математическое ожидание Хср=0,0041663

Среднее квадратическое отклонение SKO=0,0001517

Действительное значение измеряемой величины = 0,005

(используется для вычисления поправки на систематику)

При соблюдении неравенства для определения значимости систематической составляющей погрешности измерений данная составляющая значима

0.0049162 < 0.005 < 0.0051517

Поправка на систематическую составляющую погрешности вводится.

Поправки:

0,0006630
0,0007640
0,0010570
0,0007470
0,0010400
0,0009520
0,0009960
0,0007100
0,0006570
0,0007370
0,0006590
0,0010090
0,0009190
0,0006960
0,0009000

Средняя поправка: 0,00083373

Исправленные результаты измерений:

N	Х	Хср-Х	(Хср-Х)2
1	0,00517073	-0,00017073	0,0000000291
2	0,00506973	-0,00006973	0,0000000049
3	0,00477673	0,00022327	0,0000000498
4	0,00508673	-0,00008673	0,0000000075
5	0,00479373	0,00020627	0,0000000425
6	0,00488173	0,00011827	0,0000000140
7	0,00483773	0,00016227	0,0000000263
8	0,00512373	-0,00012373	0,0000000153
9	0,00517673	-0,00009673	0,0000000094
10	0,00509673	-0,00009673	0,0000000094
11	0,00517473	-0,00017473	0,0000000305
12	0,00482473	0,00017527	0,0000000307
13	0,00491473	0,00008527	0,0000000073
14	0,00513773	-0,00013773	0,0000000190
15	0,00493373	0,00006627	0,0000000044

Математическое ожидание Хср=0.005

Среднее квадратическое отклонение SKO=0.0001517

Случайная составляющая погрешности измерений: 0.000084

Случайная составляющая погрешности измерений,

проводимых с двумя параллельными определениями:0.001362

Систематическая составляющая погрешности измерений: 0.0008337

Значима.

Воспроизводимость результатов анализа:

отношение среднего к среднему квадратическому отклонению (х_ср/S): 32,9674402

отношение среднего квадратического отклонения к среднему(S/х_ср) : 0,030333

относительная погрешность в % (100*Δx/M): 3,033295866

Предел обнаружения метода (утроенное значение SKO): 0,0004550