5. Факультативный материал

Задача 5.1.: Использование Excel для расчёта простых процентов по депозиту.

Excel незаменим для решения целого ряда финансовых задач. Предположим, организация располагает некоторыми оборотными средствами, или наоборот для модернизации оборудования их не хватает. Какой будет ежемесячный платёж по кредитам и депозитам? Повторите задачу с использованием функции СЕГОДНЯ, вычислением количества прошедших дней и суммы начисленных процентов. С использованием условного форматирования, добейтесь того, чтобы когда до окончания вклада остается меньше 15 дней значения в столбце I4:I8 заливались красным цветом.

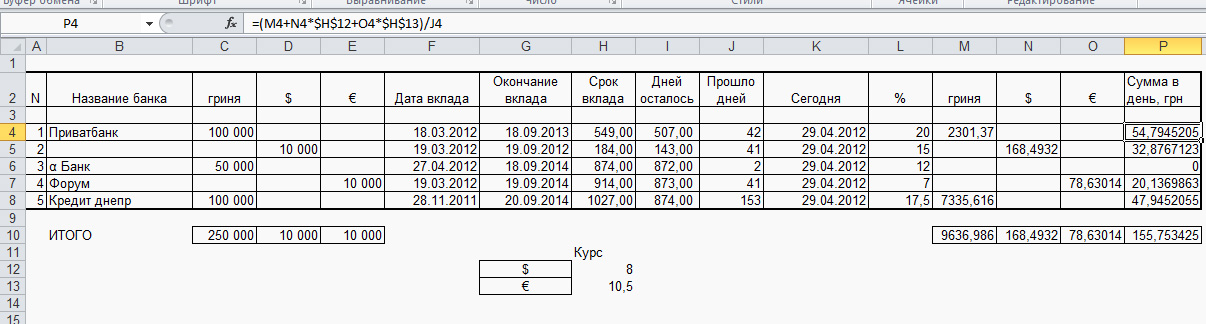
Самостоятельно вычислите, хватит ли у организации денег на покупку очистного оборудования стоимостью 450 000 грн. На какой момент денег будет достаточно, при условии, что все депозитные договора оформлены как «Вільній рух»?

Задача 5.2.: Используя Excel для расчёта выплат по кредиту найти оптимальный банковский кредит на покупку скруббера бутары СБ-60 стоимостью 75 000 грн.

Д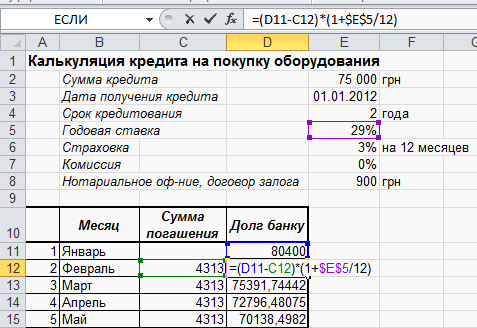 анная задача решается самостоятельно и начинается с анализа рынка банковских кредитов. Выбирается оптимальный, с минимальной переплатой и возможностью досрочного расторжения. Учтите, что фраза без скрытых комиссий и переплат на практике часто оказывается просто маркетинговым ходом. На банковских сайтах часто предлагаются свои калькуляторы для расчета ежемесячного взноса по кредиту. Создайте свой пример калькуляции и сравните с предложениями банков. Вычислите сумму переплат за 2 года, за 5 лет и за 10.

Задача 5.3.: Решение дифференциальных уравнений

Дифференциальные уравнения могут быть использованы для моделирования как экологических так и социальных и экономических процессов. Проведем исследование системы нелинейных дифференциальных уравнений, отражающих известную экологическую задачу: на ограниченной территории в единицу времени вырастает определенное количество моркови (здесь Eo=1000), появляются 10 зайцев и начинают размножаться со скоростью N*kr, съедая моркови ed=N*ke, при этом остается Е моркови. Когда вся морковь съедается и образуется дефицит D=E-Eo, зайцы начинают вымирать со скоростью, пропорциональной их количеству и квадрату дефицита D: vs=N*ks* D² . Получаем систему уравнений:

dN/dt = kr*N - ks*N* D ²

E=1000- ke*N

D= ЕСЛИ(E>1000; (E-Eo)/N;0)

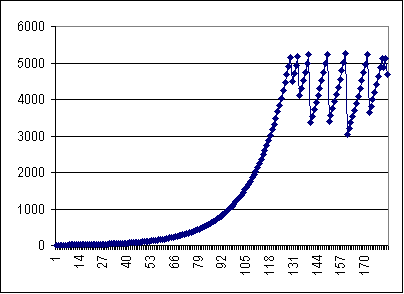
Присвойте ячейкам строки 3 имена соответствующих коэффициентов и заполните строку 7 таблицы формулами: A7=A6+B7-C7; B7=kr*A6;

C7= ks*A6*E7^2; D7=ke*A6; E7=ЕСЛИ(F7>Eo;( F7-Eo)/A6; 0); F7=Eo-D7. Скопируйте вниз всю строку 7. Постройте графики и исследуйте поведение N, vr, vs, ed, E. Исследуйте поведение системы при различных зависимостях dN/dt от D: линейной, логарифмической, показательной и т.д.

	A	B	C	D	E	F
2	нач.кол	kr	ks	ke	Eo
3	10	0,05	5000	0,2	1000
4
5	N	vr	vs	ed	дефицит	E
6	10				D
7	10,5	0,5	0	2	0	998
8	11,025	0,525	0	2,1	0	997,9
9	11,57625	0,55125	0	2,205	0	997,795
10	12,15506	0,578813	0	2,31525	0	997,6848
11	12,76282	0,607753	0	2,431013	0	997,569
12	13,40096	0,638141	0	2,552563	0	997,4474
13	14,071	0,670048	0	2,680191	0	997,3198
14	14,77455	0,70355	0	2,814201	0	997,1858
15	15,51328	0,738728	0	2,954911	0	997,0451
16	16,28895	0,775664	0	3,102656	0	996,8973
17	17,10339	0,814447	0	3,257789	0	996,7422
18	17,95856	0,85517	0	3,420679	0	996,5793
19	18,85649	0,897928	0	3,591713	0	996,4083
20	19,79932	0,942825	0	3,771298	0	996,2287
21	20,78928	0,989966	0	3,959863	0	996,0401
22	21,82875	1,039464	0	4,157856	0	995,8421
23	22,92018	1,091437	0	4,365749	0	995,6343
24	24,06619	1,146009	0	4,584037	0	995,416
25	25,2695	1,20331	0	4,813238	0	995,1868
26	26,53298	1,263475	0	5,0539	0	994,9461
27	27,85963	1,326649	0	5,306595	0	994,6934
28	29,25261	1,392981	0	5,571925	0	994,4281
29	30,71524	1,46263	0	5,850521	0	994,1495
30	32,251	1,535762	0	6,143048	0	993,857
31	33,86355	1,61255	0	6,4502	0	993,5498