
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Привести кривую к каноническому виду:
- •Найти уравнения линий пересечения данной поверхности с координатными плоскостями . Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 14
- •Вариант 15
- •Построить кривую
- •Привести кривую к каноническому виду:
- •Найти уравнения линий пересечения данной поверхности с координатными плоскостями . Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
Вариант 8
ABCDEF – правильный шестиугольник, причем =
 ,
,
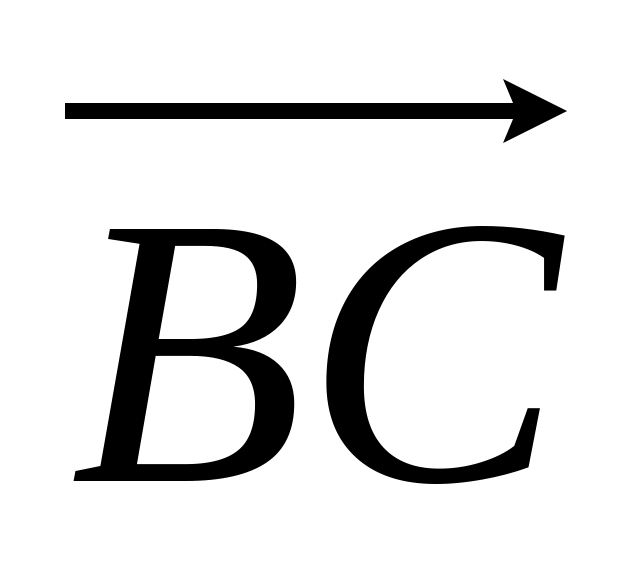 =
= .
Выразить через
и
векторы
.
Выразить через
и
векторы
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
,
,
 .
.Найти угол, образованный единичными векторами
 если известно, что векторы
если известно, что векторы
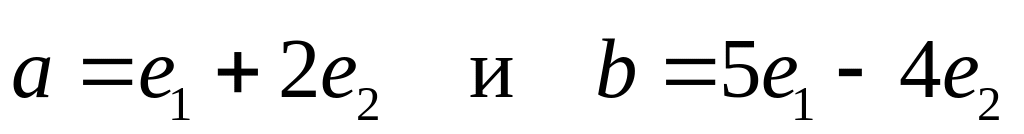 перпендикулярны
перпендикулярныНайти тупой угол (в радианах) между диагоналями параллелограмма, построенного на векторах
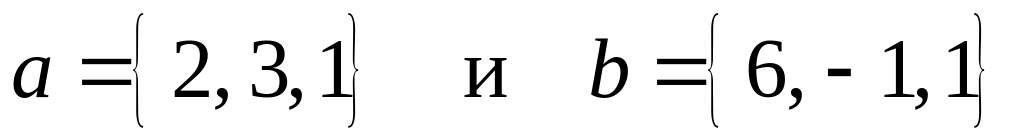 .
.Найти уравнения и длины сторон треугольника, если даны две вершины треугольника А(-1, -1), В(-11, 4) и точка пересечения высот К(-7, -4).
Построить кривую
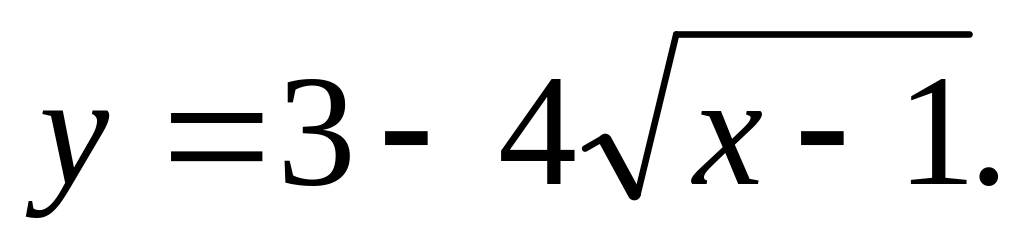
Привести кривую к каноническому виду:

Найти точку, симметричную точке М относительно прямой L

Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям
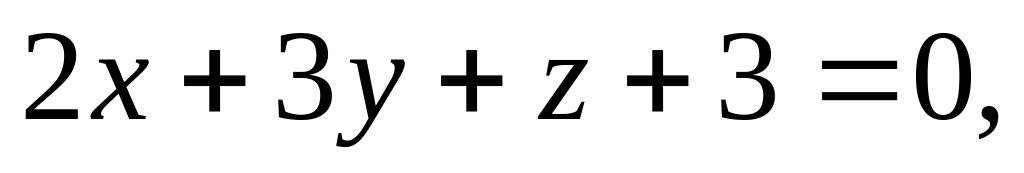

Докажите, что прямая
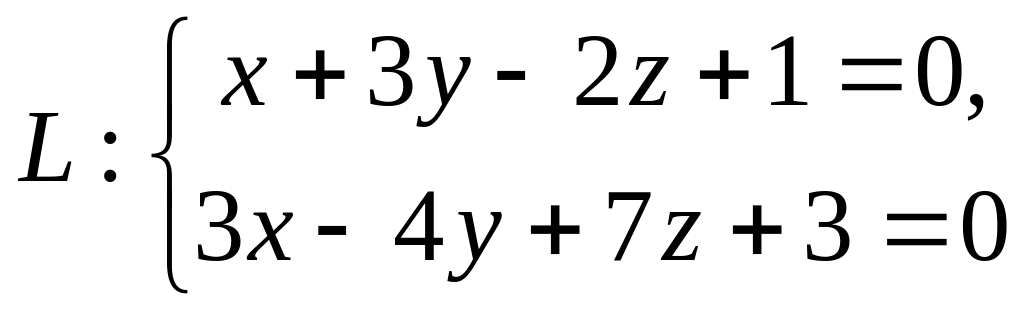 пересекает ось OX.
пересекает ось OX.Составьте уравнения прямых, образованных пересечением плоскости
 с координатными плоскостями.
с координатными плоскостями.Составить уравнение сферы, если известно, что точки
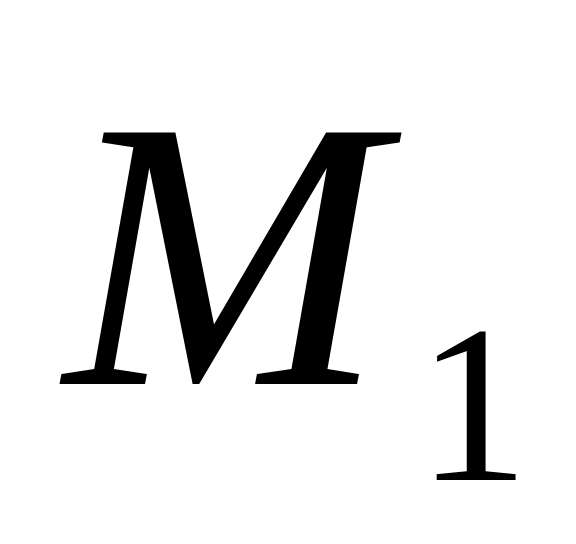 (3;-3;2)
(3;-3;2) и
и
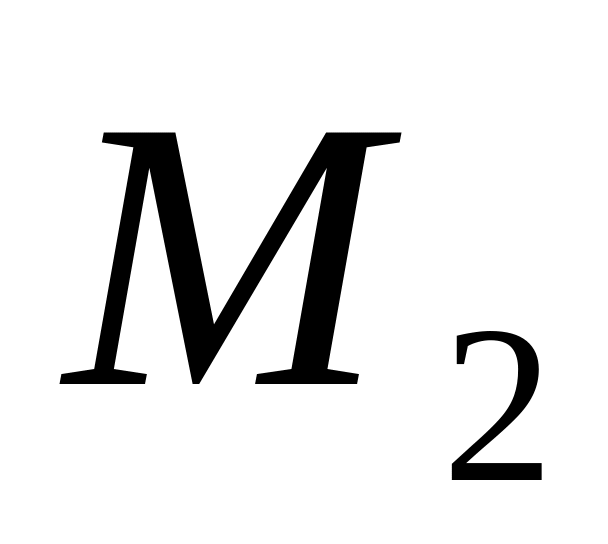 (5;3;-6)
- концы диаметра сферы.
(5;3;-6)
- концы диаметра сферы.Найти уравнения линий пересечения данной поверхности с координатными плоскостями
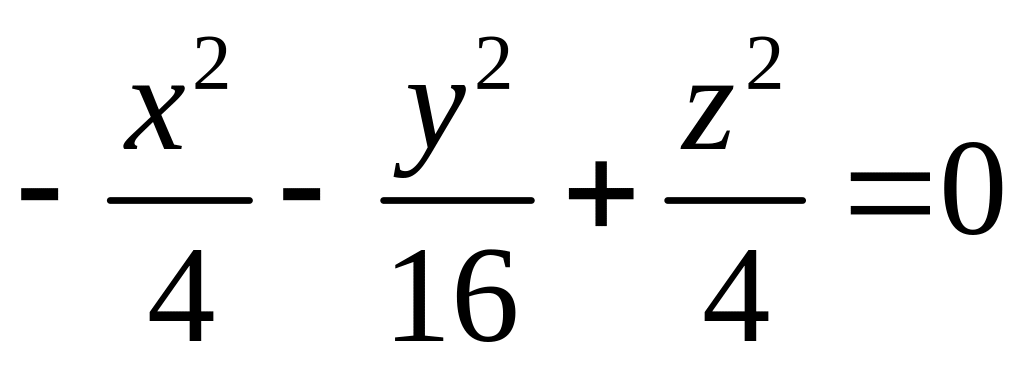
Вариант 9
В пространстве заданы треугольники ABC и
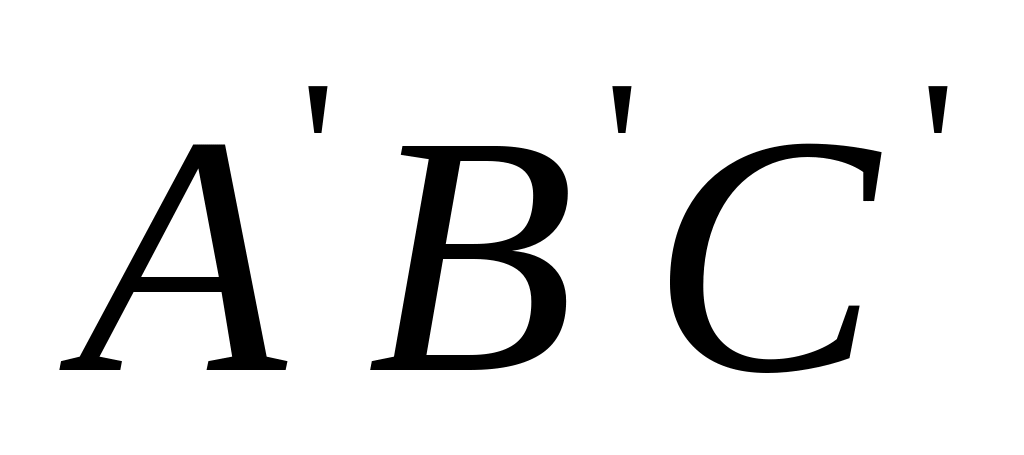 .
M
и
.
M
и
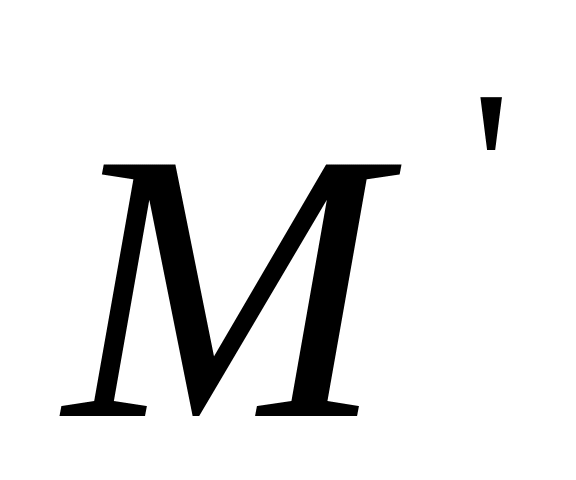 – точки пересечения их медиан. Выразить
– точки пересечения их медиан. Выразить
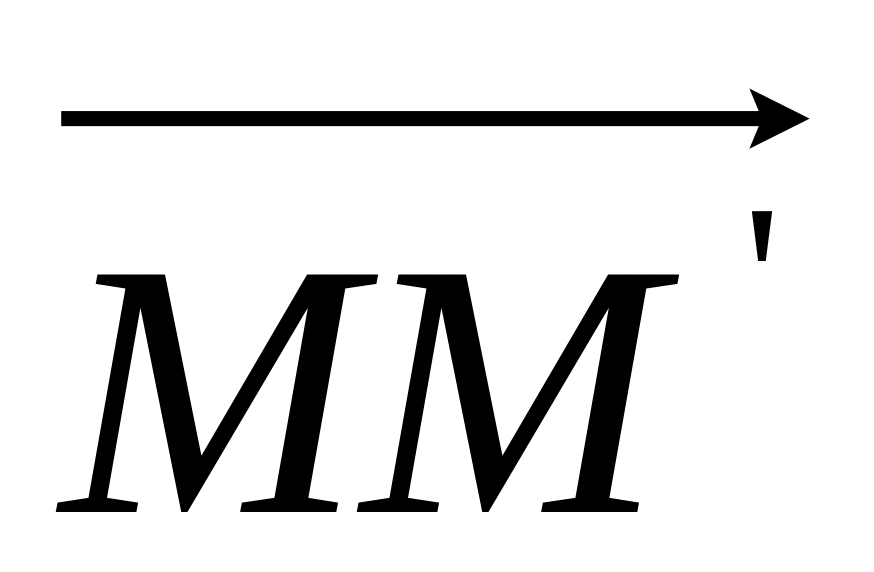 через
векторы
через
векторы
 ,
,
 и
и
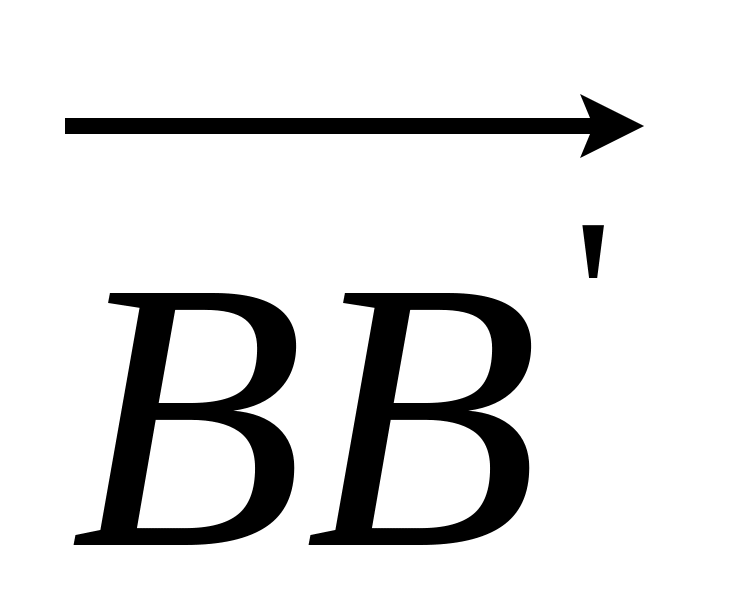
Доказать, что вектор
 перпендикулярен вектору
перпендикулярен вектору
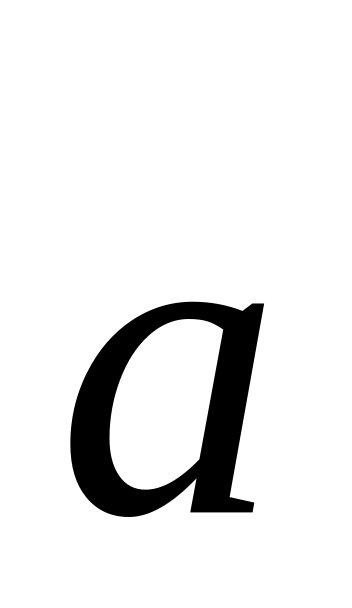 .
.Найти вектор
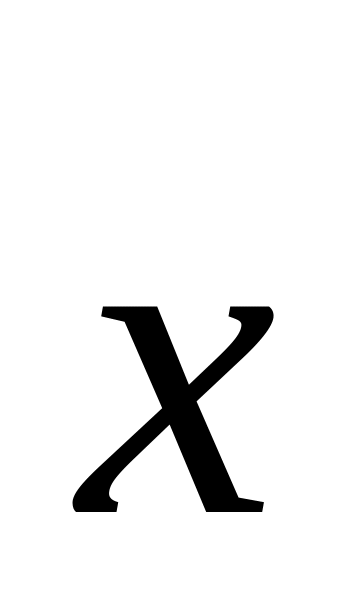 ,
коллинеарный вектору
,
коллинеарный вектору
 ,
если его проекция на вектор
,
если его проекция на вектор
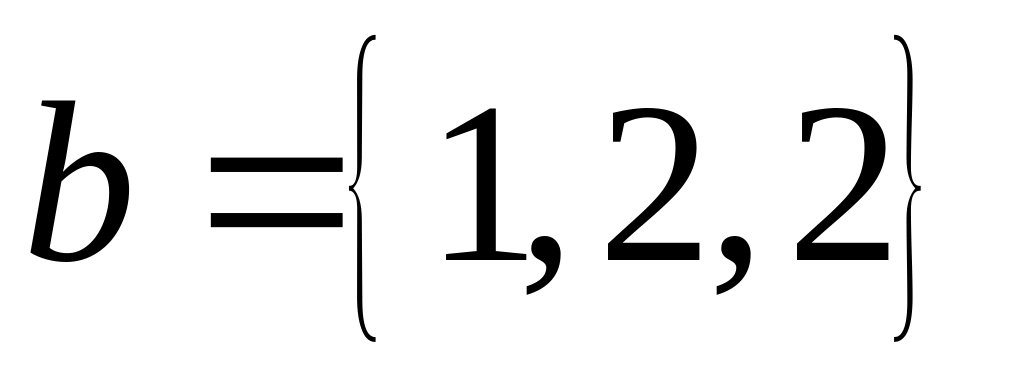 равна 5.
равна 5.Найти координаты вершин треугольника, если даны уравнения двух сторон треугольника и двух высот: (АС): х-2у+1=0 2х-4у+2=0 (АВ): х+2у-3=0 2х-у-19=0.
Построить кривую
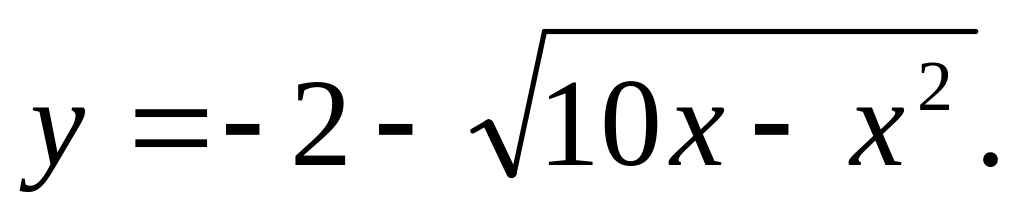
Привести кривую к каноническому виду:
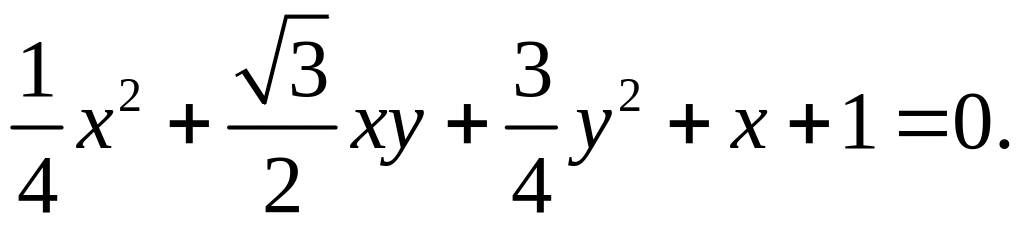
Найти точку , симметричную точке М относительно прямой L, если

Составьте уравнение плоскости, которая проходит через точку
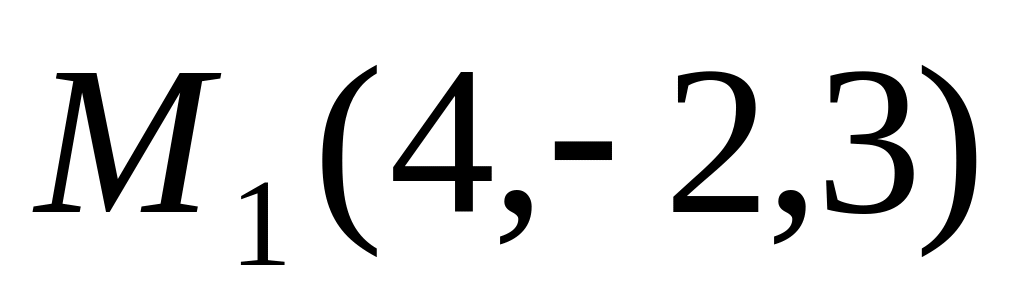 перпендикулярно к двум плоскостям:
перпендикулярно к двум плоскостям:
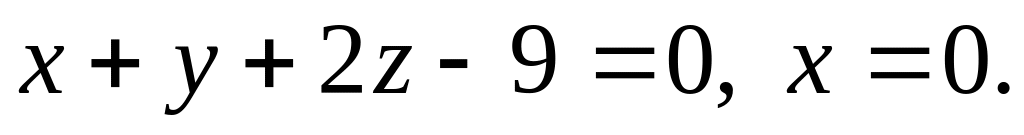 .
.Составьте уравнение плоскости, проходящей через прямую
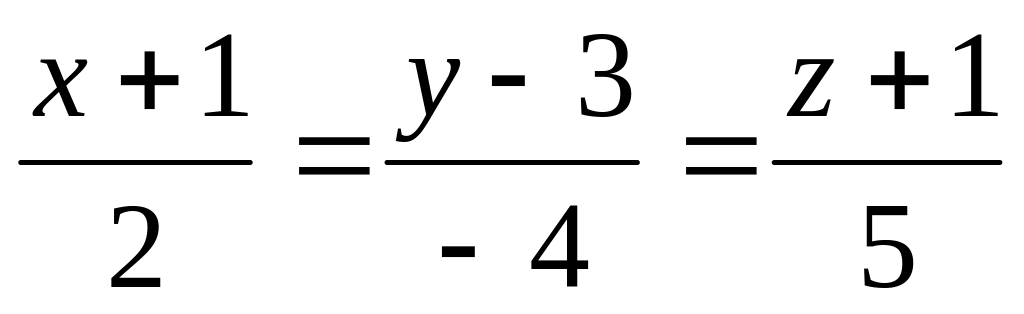 перпендикулярно к плоскости
перпендикулярно к плоскости
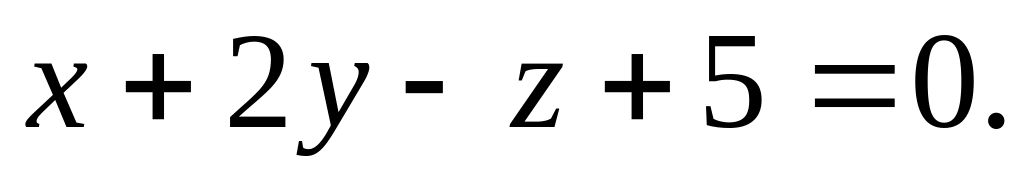
Проверить параллельность прямых или найти угол между ними:
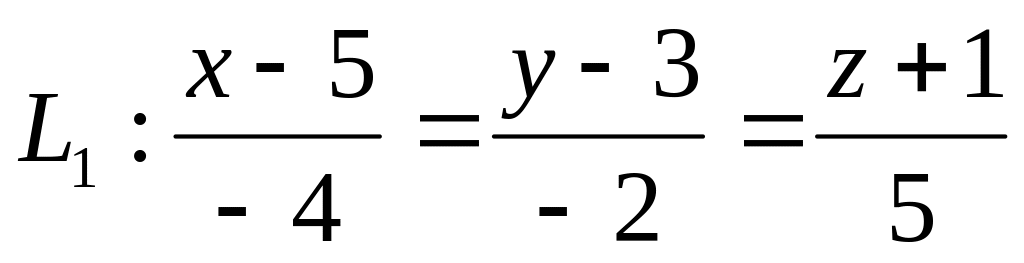 и
и
Составить уравнение сферы, если известны координаты центра С(1;-4;-1) и плоскость 2x – y + 2z + 2 = 0 касается сферы.
Найти уравнения линий пересечения данной поверхности с координатными плоскостями
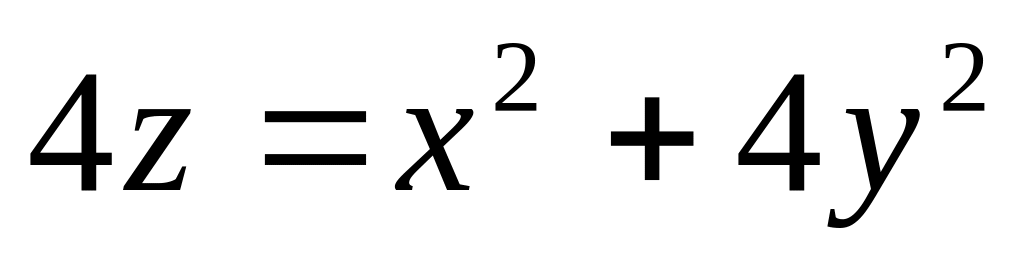 .
.
Вариант 10
Точки E и F – середины сторон AD и BC четырехугольника ABCD. Доказать, что =
 (
+
(
+ ).
).Для заданных векторов
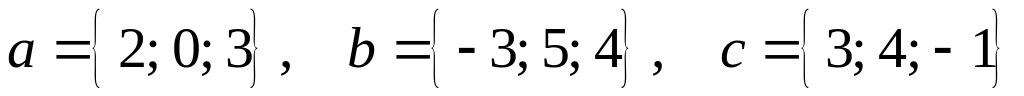 вычислить проекцию вектора
вычислить проекцию вектора
 на вектор
на вектор
 .
.Упростить выражение

Найти уравнения и длины сторон и медиан треугольника если даны две вершины треугольника А(-1, 1), В(19, -9), и точка пересечения медиан М(29/3; -1/3).
Построить кривую
 .
.Привести кривую к каноническому виду:

Найти точку, симметричную точке М относительно прямой L, если

Определите двугранный угол, образованный пересечением пары плоскостей
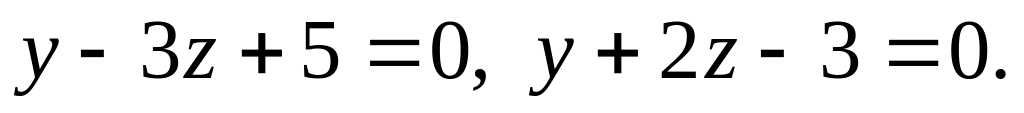
Вычислите кратчайшее расстояние между прямыми:
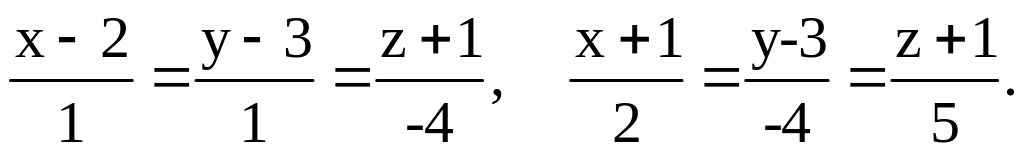
Составьте уравнения проекции прямой
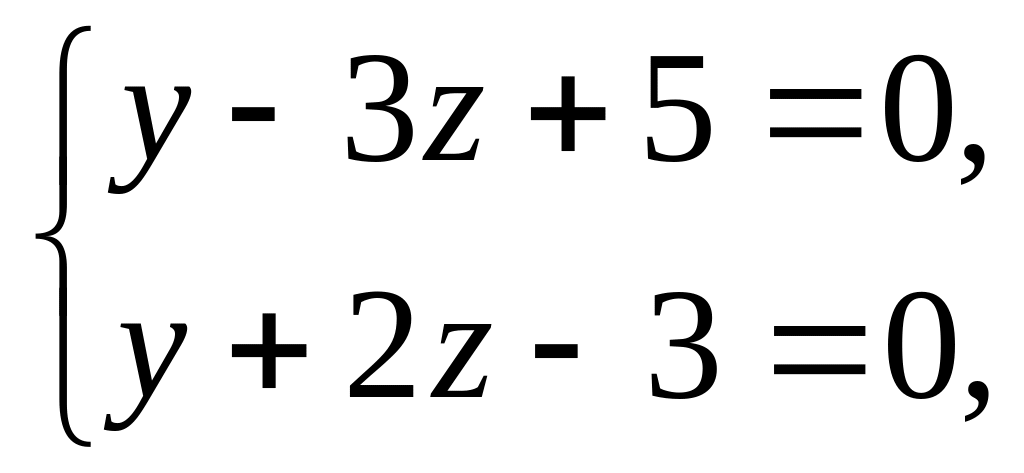 на плоскость
на плоскость
 .
.Составить уравнение сферы, если известно, что точки
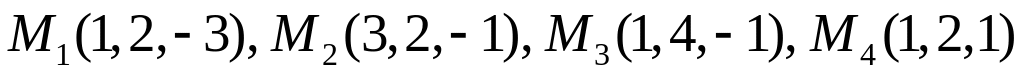 лежат на сфере.
лежат на сфере.Найти уравнения линий пересечения данной поверхности с координатными плоскостями
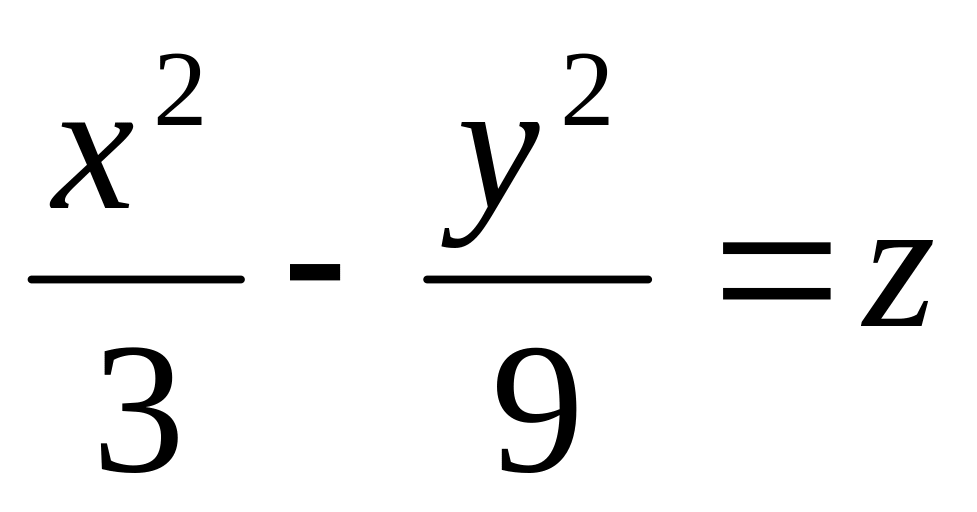 .
.
