4. Дифференцируемость функции. Связь дифференцируемости с существованием производной и непрерывностью функции

Определение 3. Функция y = f(x) называется дифференцируемой в точке xD(f), если она определена в некоторой окрестности точки x и её приращение в этой точке можно представить в виде:

x = Ax + (x)x,

где A = A(x) – не зависит от x; (x) – бесконечно малая величина при x0, т.е.

Теорема 1 (связь дифференцируемости с существованием производной)

Функция y = f(x) дифференцируема в точке xD(f) тогда и только тогда, когда она имеет в этой точке производную f '(x). При этом f '(x) = A.

Доказательство.

1) Необходимость: Дано: y = f(x) дифференцируема в точке х.

Доказать: A = f '(x).

Так как функция y = f(x) дифференцируема в точке х, то по определению

y = A  x + (x)  x,

где (x)  0 при x  0.

Разделим это равенство на x ≠ 0:

.

Перейдём к пределу при x  0:

существует, а значит f '(x) = A.

Необходимость доказана.

2) Достаточность: Дано: f ' (x) – существует

Доказать: f(x) дифференцируема.

Так как существует f '(x)= , то по свойству предела можно записать:

,

где (x)  0 при  x 0.

Умножим это равенство на x:

 функция y = f(x), дифференцируема в точке х.

Достаточность доказана.

Теорема 2 (связь дифференцируемости с непрерывностью функции)

Если функция y = f(x) дифференцируема в точке xD(f), то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то её приращение в этой точке можно представить в виде:

y = A  x + (x)  x,

где A = f '(x) и (x)  0 при x  0.

Найдём предел от y при x  0:

Отсюда следует, что по определению 2 непрерывности функции в точке функция y = f(x) непрерывна в точке x.

Замечание. Обратное теореме 2 утверждение не всегда верно.

5. Правила дифференцирования

Теорема 3. Если функции U(x) и V(x) дифференцируемы в точке x, то функция U(x)  V(x) дифференцируема в точке x и её производная вычисляется по формуле:

(U(x)  V(x))' = (U(x))'  (V(x))'.

Доказательство: Рассмотрим функцию y = U(x)  V(x).

Тогда y = U  V. Разделим на x и перейдём к пределу при x  0:

так как по условию теоремы функции U(x) и V(x) дифференцируемы.

Значит, (U(x)  V(x))' = U '(x)  V '(x).

Теорема доказана.

Теорема 4. Если функции U(x) и V(x) дифференцируемы в точке х, то функция (U(x)V(x)) дифференцируема в точке х и её производная вычисляется по формуле:

(U(x)  V(x))' = (U(x))' V(x) + U(x)  (V(x))'.

Доказательство. Рассмотрим функцию . Найдём её приращение

y = (U+U)(V+V) – UV = UV + UV + VDU + DUDV – UV=

= UDV + VDU + DUDV.

Разделим Dy на Dx и перейдем к пределу при Dx  0:

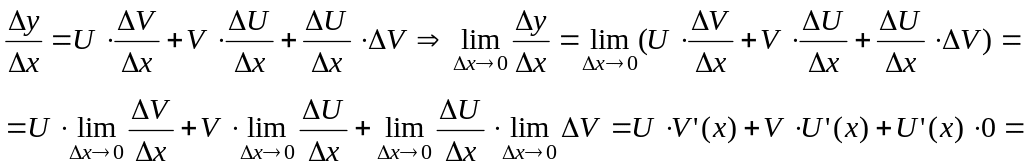
так как по условию функции U(x) и V(x) дифференцируемы, а значит , и .

Следовательно,

(U(x) V(x))' = U ' (x)  V(x) + U(x)  V ' (x).

Теорема доказана.

Следствия:

а) Если U(x), V(x) и W(x) дифференцируемы в точке х, то функция (U(x)V(x) W(x)) дифференцируема в точке х и её производная вычисляется по формуле:

(UV×W)' = U '×V×W + U×V '×W + U×V×W '.

б) Производная постоянной, умноженной на дифференцируемую функцию, равна этой постоянной, умноженной на производную функции:

(C×U(x))' = C×U ' (x).

Теорема 5. Если функции U(x) и V(x) дифференцируемы в точке х и V(x) ≠ 0, то функция дифференцируема в точке х и её производная вычисляется по формуле:

.

Доказательство. Рассмотрим функцию . Найдём её приращение

Разделим y на x и перейдём к пределу при x  0:

,

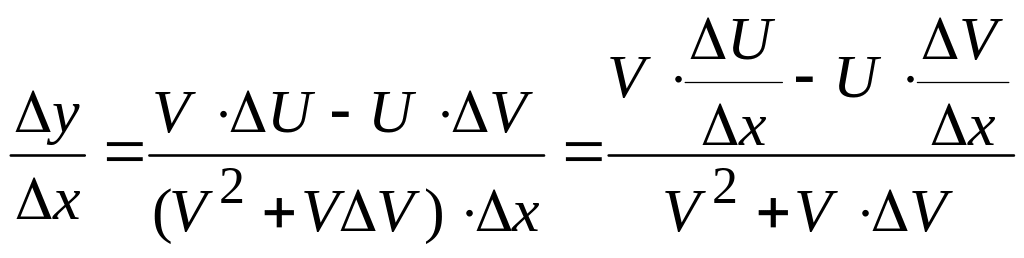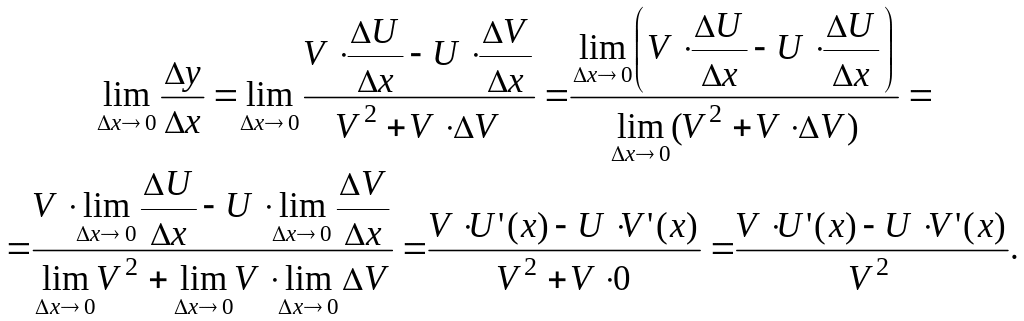
Значит,

.

Теорема доказана.

Теорема 6 (производная сложной функции). Если функция f(u) дифференцируема в точке u, а функция u(x) дифференцируема в точке x, причём u = u(x), тогда сложная функция f(u(x)) дифференцируема в точке x и её производная вычисляется по формуле:

(f (u(x)))' = f '(u) ×u' (x).

Доказательство. Рассмотрим функцию y = f(u). Так как функция f(u) дифференцируема в точке u, то её приращение можно записать в виде:

,

где .

Разделим на Dx и перейдём к пределу при Dx  0:

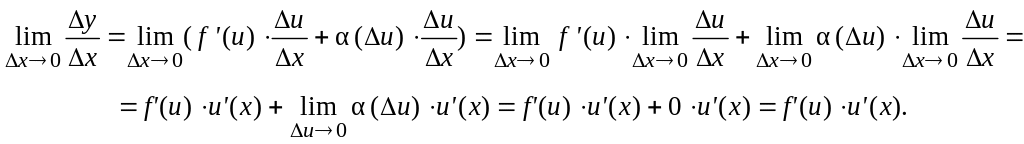
Если D x 0, то D u 0, так как u(x) дифференцируема, а значит непрерывна, т.е.

(f(u(x)))' = f ' (u) ×u' (x).

Теорема доказана.