§ 2. Предел функции

1. Предел функции в конечной точке x0

Определение 1. Окрестностью точки x₀ называется любой интервал, содержащий точку x₀:

.

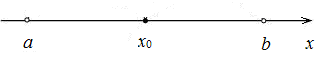
Определение 2. -Окрестностью точки x₀ называется интервал ( ; ), длина которого 2, симметричный относительно x₀:

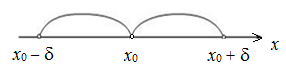
Определение 3. Проколотой -окрестностью точки x₀ называется -окрестность точки x₀ без самой точки x₀:

Определение 4. Число А называется пределом функции f(x) при x  x₀, если для любого малого числа ε > 0 существует такое малое число , что для любого x, принадлежащего D(f) и проколотой δ-окрестности точки x₀, т.е. , выполняется неравенство: .

Итак: и .

2. Односторонние пределы

Определение 5. Число А называется правым (левым) пределом функции y = f(x) в точке x₀, если для любого малого числа ε > 0 найдётся другое малое число – такое, что для всех и лежащих в правой (левой) окрестности точки x₀, т.е. , справедливо неравенство: .

При этом используют следующие обозначения:

– для правого предела.

– для левого предела.

Замечание 1. Если f(x) имеет в точке x₀, предел равный А, то существуют и и справедливо равенство:

.

Замечание 2. Если f(x) имеет в точке x₀ правый и левый пределы, равные между собой, то в точке функция f(x) имеет предел, равный числу:

.

Замечание 3. Если f(x) имеет в точке x₀ правый и левый пределы, но они не равны между собой, то в точке x₀ функция f(x) не имеет предела.

3. Предел функции на бесконечности

Определение 6. Окрестностью бесконечно удалённой точки называют множество значений x, удовлетворяющих неравенству , где N достаточно большое положительное число.

Определение 7. Число А называется пределом функции f(x) при , если для любого малого числа ε > 0 существует другое большое число – такое, что для любого удовлетворяющего неравенству выполняется неравенство . Этот факт

записывают: .

4. Бесконечно малые и бесконечно большие функции

Определение 8. Функция (x) называется бесконечно малой при x  x₀ или в точке , если предел (x) при x равен нулю: .

Определение 9. Функция f(x) называется бесконечно большой в точке , если предел f(x) при x  x₀ равен ∞. Это значит, что для любого сколь угодно большого числа M > 0 существует малое число δ = δ(M) > 0 такое, что для любого удовлетворяющего неравенству , выполняется неравенство f(x) > M.

Определение 10. Функция f(x) называется ограниченной на некотором множестве X  D(f), если существует такое число M > 0, что для любого x  X выполняется неравенство f(x) < M.

Основные свойства бесконечно малых функций

1) Алгебраическая сумма конечного числа бесконечно малых функций в точке есть бесконечно малая функция в этой точке , т.е. если – бесконечно малые функции в точке , то – бесконечно малая функция в этой точке .

2) Произведение конечного числа бесконечно малых функций в точке есть бесконечно малая функция в точке , т.е. если – бесконечно малые функции в точке , то – бесконечно малая функция в этой точке .

3) Произведение бесконечно малой функции в точке на ограниченную функцию в некоторой окрестности точки есть бесконечно малая функция в точке , т. е. если α(x) бесконечно малая функция в точке и f(x) ограниченная в некоторой окрестности точки , то α(x)f(x) – бесконечно малая функция в точке .

Следствие из свойства 3). Произведение постоянной c на бесконечно малую функцию α(x) в точке есть бесконечно малая функция в точке , т.е. если α(x) – бесконечно малая функция в точке , то с×α(x) – бесконечно малая функция в точке x₀.

Теорема (о связи между бесконечно малой функцией в точке x₀ и бесконечно большой функцией в точке x₀)

Если функция f(x) является бесконечно большой в точке , то функция является бесконечно малой в точке . (Верно и обратное утверждение)