10. Условный экстремум. Множители Лагранжа

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение

(х, у) = 0,

которое называется уравнением связи.

Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.

Тогда u = f(x, y(x)).

.

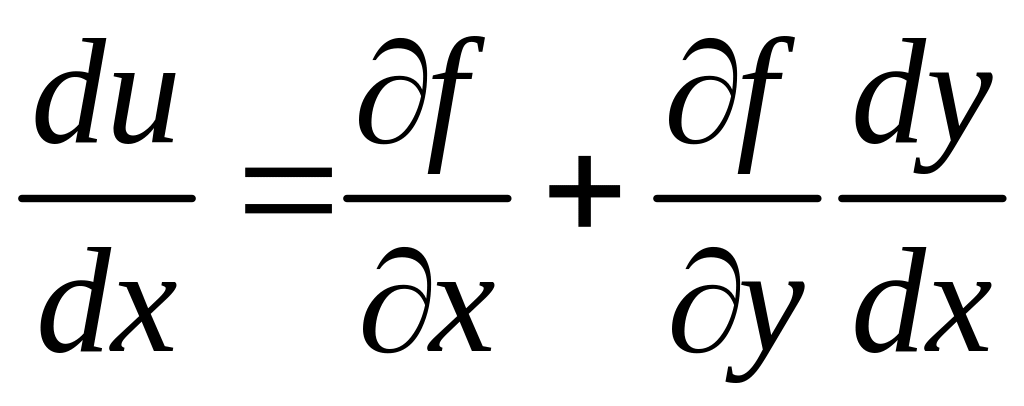В точках экстремума:

(1)

Кроме того:

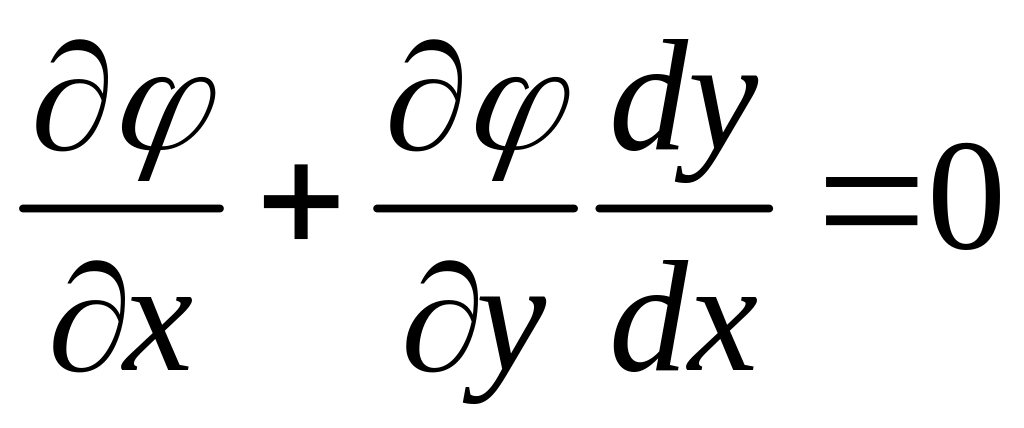(2)

Умножим равенство (2) на число  и сложим с равенством (1).

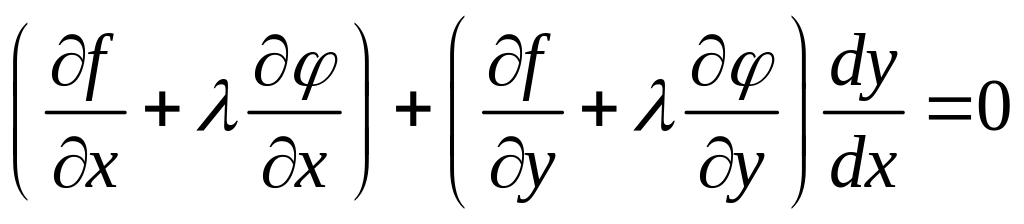
Для выполнения этого условия во всех точках найдем неопределенный коэффициент  так, чтобы выполнялась система трех уравнений:

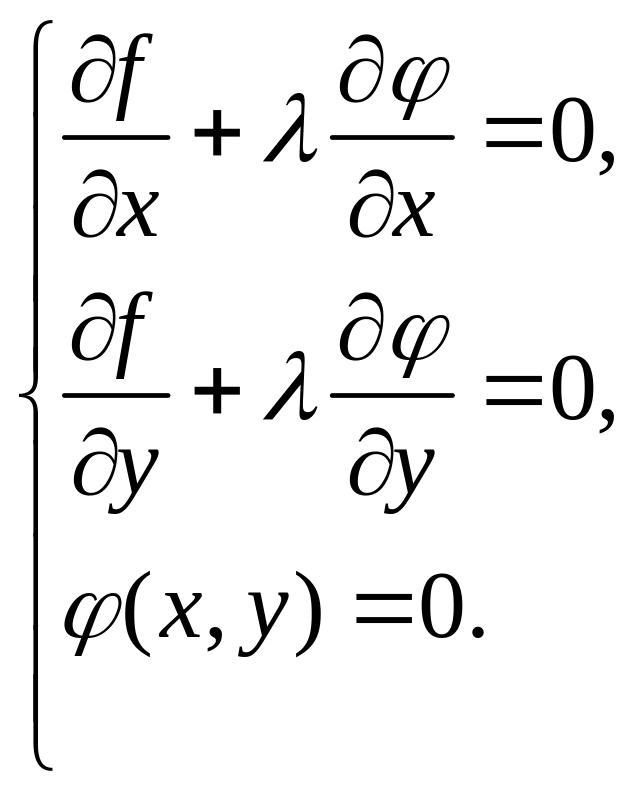
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Выражение u = f(x, y) + (x, y) называется функцией Лагранжа.

Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0

Таким образом, функция имеет экстремум в точке .

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.

11. Примеры функций многих переменных в экономике

1) Функция полезности, выражающая полезность от двух приобретенных товаров и чаще всего встречается в следующих видах:

а) , где ( ), , ;

б) , где , ( ), , ; такую функцию называют функцией постоянной эластичности;

в) функция Р. Стоуна , где ( ) – минимально необходимое количество -го блага, которое приобретается в любом случае; ( ) – коэффициенты, характеризующие относительную ценность благ для потребителя.

2) Производственная функция, выражающая результат производственной деятельности от обусловивших его факторов (например, труда и капитала ), чаще всего встречается в следующих видах:

а) функция Кобба–Дугласа ;

б) функция с постоянной эластичностью замещения .

Замечание. Приведенные функции могут быть обобщены на любое число переменных.

Определение 9. Линией уровня функции двух переменных называют плоскую кривую, получаемую при пересечении графика этой функции плоскостью ( ), параллельной координатной плоскости .

Замечание 1. Обычно линии уровня, соответствующие различным значениям , проецируются на координатную плоскость . В этом случае с их помощью удобно исследовать сложный характер графика функции . Таким образом, можно сказать, что линии уровня функции – это семейство кривых на координатной плоскости , описываемое уравнением вида .

Замечание 2. В экономике линии уровня производственных функций называют изоквантами (линиями постоянного уровня производства), а линии уровня функции полезности – кривыми безразличия (вдоль них полезность двух товаров остается неизменной)

Пример. Найти линии уровня функции .

Решение. Линии уровня данной функции – это семейство кривых на плоскости , описываемое уравнением . Преобразуем это уравнение: выделим полный квадрат по каждой переменной. Тогда или . Полученное уравнение описывает семейство окружностей с центром в точке радиуса ( ).