Полный дифференциал функции двух переменных, его применение в приближенных вычислениях

Пусть требуется вычислить приближенно число как значение функции в некоторой точке , т. е. . Предполагается, что без применения вычислительных средств этого сделать нельзя для точки , но можно сделать для некоторой близкой к ней точке (ее назовем "удобной" точкой).

В этом случае справедлива следующая формула:

, (3.1)

где – приращения аргументов, – значения частных производных от функции в точке .

Пример 3. Вычислить приближенно число , используя функцию нескольких переменных.

Решение: Возьмем функцию . Тогда , , . Выбираем два числа 3 и 2, близкие к числам 2,97 и 2,02, следовательно "удобная" точка , так как в этой точке точно вычисляется значение нашей функции: . Тогда приращения равны .

Чтобы применить формулу (3.1), необходимо найти значения частных производных от функции по каждому аргументу в точке . Сначала ищем частные производные , :

,

.

Тогда формула (3.1) примет вид

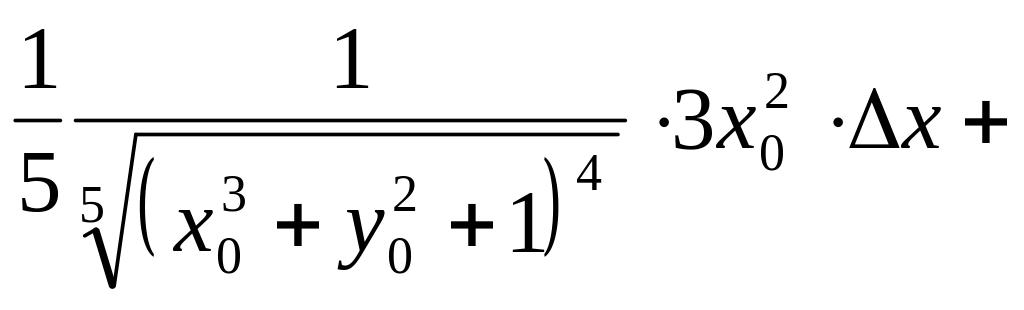
+ . (3.2)

Подставляем в , вместо точку :

,

.

Окончательно, подставляя в равенство (3.2), все необходимые данные, получим 1,9909.

4. Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности

нормаль

N

 N₀

касательная плоскость

Пусть N и N₀ – точки данной поверхности. Проведем прямую NN₀. Плоскость, которая проходит через точку N₀, называется касательной плоскостью к поверхности, если угол между секущей NN₀ и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN₀.

Определение. Нормалью к поверхности в точке N₀ называется прямая, проходящая через точку N₀ перпендикулярно касательной плоскости к этой поверхности.

В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.

Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М₀(х₀, у₀), касательная плоскость в точке N₀(x₀,y_0,(x₀,y₀)) существует и имеет уравнение:

.

Уравнение нормали к поверхности в этой точке:

Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х₀, у₀) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х₀, у₀) к точке (х₀+х, у₀+у).

Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.

Пример. Написать уравнения касательной плоскости и нормали к поверхности в точке М(1, 1, 1).

Решение.

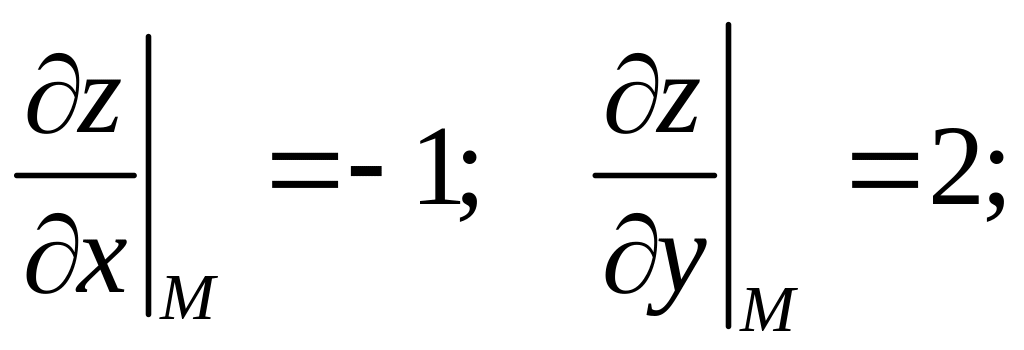
Уравнение касательной плоскости:

Уравнение нормали:

5. Производные и дифференциалы высших порядков функции нескольких переменных

Пусть функция имеет частные производные и 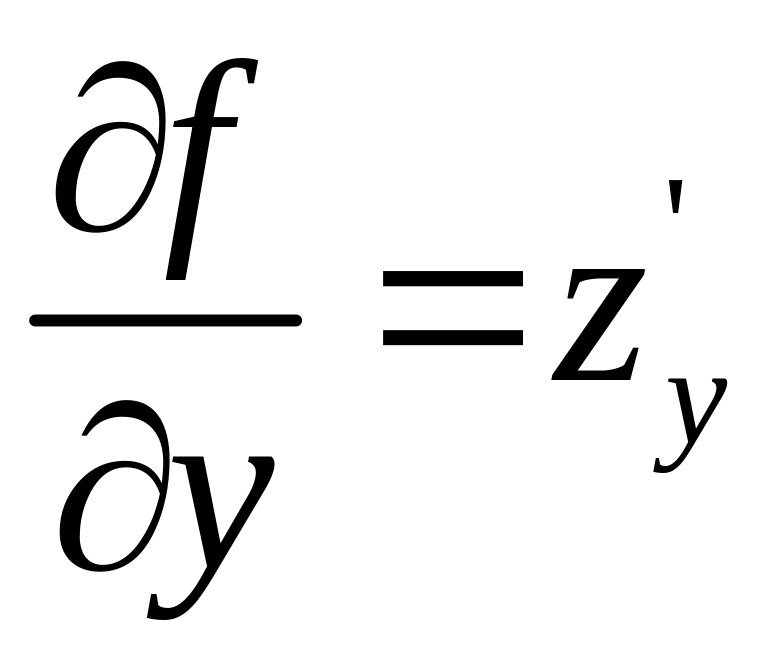. Каждая из них, являясь функцией двух переменных, может, в свою очередь, иметь частные производные

.

Эти производные обозначаются также

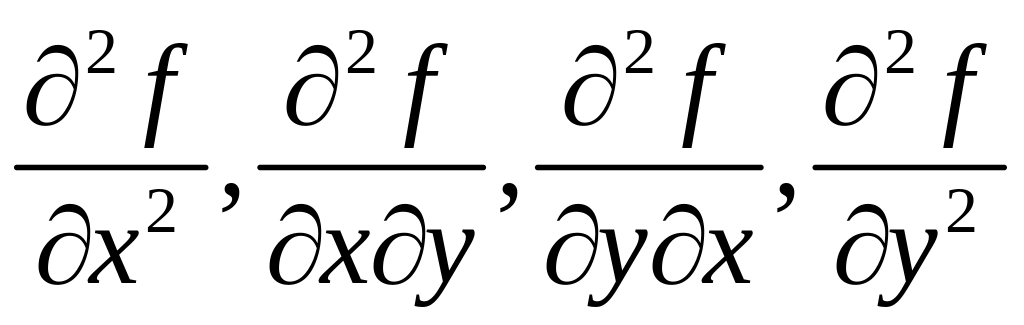
и называются производными второго порядка. При этом называются смешанными производными.

Нахождение этих производных осуществляется по правилам, описанным выше.

Пример 1. ; найти все производные второго порядка.

, , ,

, , .

Из примера следует, что , то есть смешанные производные второго порядка равны между собой. Этот факт не является случайностью.

Можно показать, что смешанные производные равны, если они непрерывны. Следовательно, в этом случае порядок дифференцирования не играет роли.

Можно рассматривать производные и более высокого порядка, например, .

При этом, как и для вторых производных, можно менять порядок двух стоящих рядом операций дифференцирования; существенным является лишь то, сколько раз по данной переменной проводится дифференцирование, порядок же роли не играет (если эти производные непрерывны). Например,

.

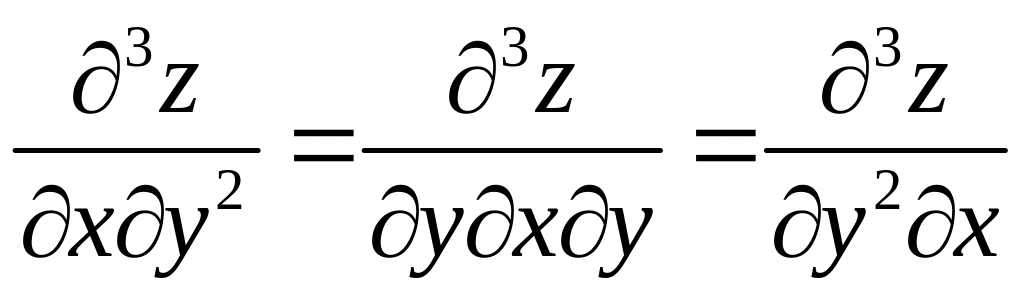Подобно тому, как рассматриваются частные производные высших порядков, можно определять и частные дифференциалы высших порядков:

, , … ,

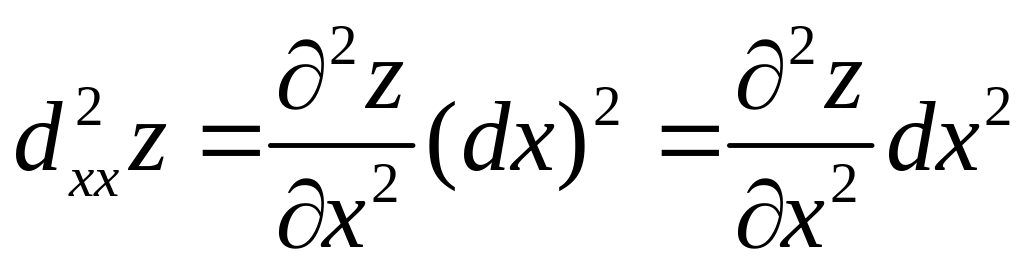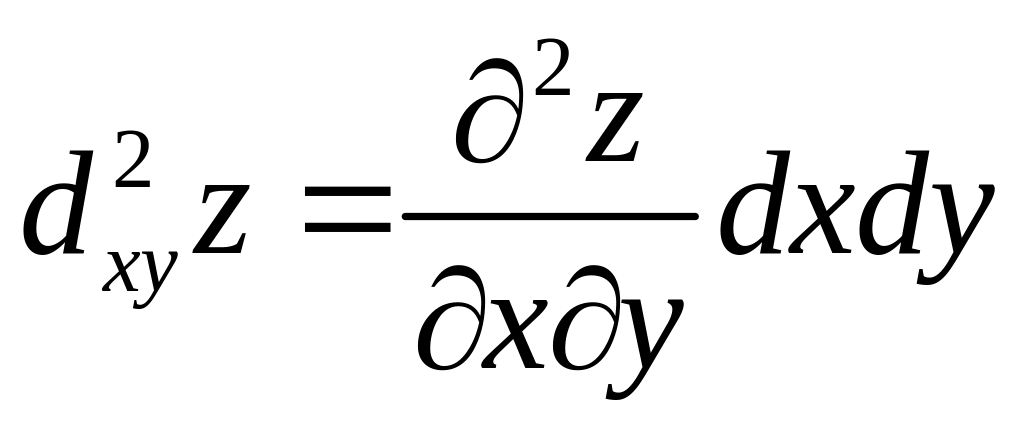где дифференциал независимой переменной х равен , дифференциал независимой переменной у равен ,….

Полный дифференциал любого порядка – это полный дифференциал от полного дифференциала предыдущего порядка. При этом при последующих дифференцированиях дифференциалы независимых переменных следует рассматривать как постоянные величины.

Пусть, например, . Тогда

,

.

Этот результат можно записать в виде символической формулы

,

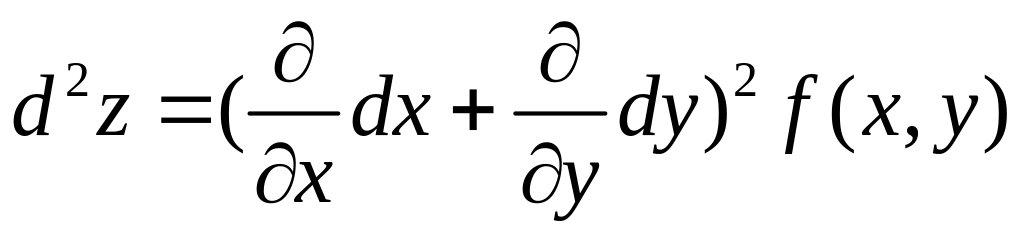где в правой части надо раскрыть скобки так, как если бы были обычными алгебраическими множителями.

Подобным же образом

.

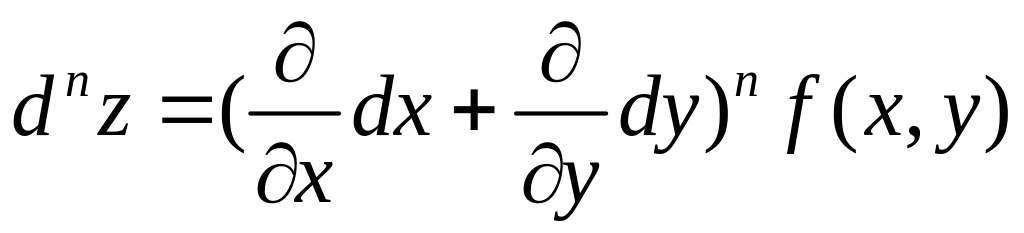Если же , но х и у не являются независимыми переменными, то форма дифференциала меняется, то есть дифференциал высшего порядка не обладает свойством инвариантности.