МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Инженерно-экономический факультет

Кафедра эконометрики и математического моделирования (ЭиММ)

ЛЕКЦИИ ПО ДИСЦИПЛИНЕ

«Математический анализ»

для направления 080100 «Экономика»

Рязань 2012

Тема 7. Дифференциальное исчисление функции нескольких переменных

и ее приложения к экономике

1. Определение функции многих переменных (ФМП), функции двух переменных (Ф2П). Геометрическое изображение Ф2П

До сих пор мы рассматривали совместное изменение двух переменных, одна из которых зависела от другой. Нередки, однако, случаи, когда независимых переменных оказывается несколько, и для определения значения функции необходимо предварительно установить значения, совместно принимаемые всеми этими независимыми переменными.

Например, объем V кругового цилиндра является функцией от радиуса R его основания и высоты H; доход предприятия зависит от объема производства, эффективности работы, возможностей сбыта; объем усеченного конуса является функцией трех переменных – радиусов R и r обоих его оснований и высоты H. Число подобных примеров можно увеличить.

Уточним понятие функции в случае нескольких независимых переменных. Говоря об изменении двух независимых переменных x и y, мы должны каждый раз указывать, какие пары значений они могут принимать совместно. Множество этих пар называется областью определения функции.

Само понятие функции дается в тех же выражениях, что и для случая одной независимой переменной.

Определение 1. Переменная z (с областью изменения ) называется функцией независимых переменных x, y в множестве D, если каждой паре их значений из D по некоторому правилу ставится в соответствие одно определенное значение .

Здесь имеется в виду однозначная функция; легко распространить это понятие и на случай многозначной функции.

Переменные x, y называются аргументами функции z. Функциональная зависимость между x, y, z обозначается аналогично случаю одной независимой переменной:

, , , ….

Например, функция определена лишь для тех пар , которые удовлетворяют условию .

Таким образом, если для функции одной переменной стандартной областью определения является промежуток (конечный или бесконечный), то для функции двух переменных мы сталкиваемся с более сложными областями определения. Рассмотрение этих областей значительно облегчается их геометрической иллюстрацией.

Для характеристики области определения функции следует указать, какая область на плоскости заполнена соответствующими точками. Сами пары чисел называют «точками». Например, для функции областью определения является круг с радиусом, равным 2, и центром в начале координат (граничные точки исключаются), то есть

.

Подобно тому, как функция геометрически иллюстрируется своим графиком, можно геометрически иллюстрировать и функцию .

И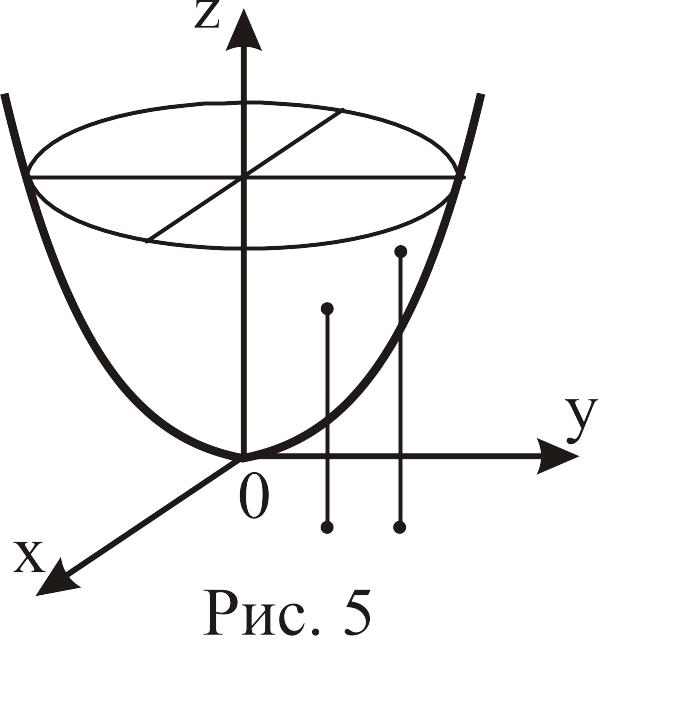 зобразив область D в плоскости , в каждой точке этой области восстановим перпендикуляр к плоскости и отложим на нем значение . Геометрическое место полученных таким образом точек и является графиком рассматриваемой функции. Это будет, вообще говоря, некоторая поверхность, а равенство называется уравнением поверхности.

Например, графиком функции является эллиптический параболоид (рис. 5).

Аналогично функции двух переменных можно рассмотреть функцию трех, четырех и большего числа переменных, так что . Определение функции и все сказанное по его поводу для случая двух переменных непосредственно переносится на случай n независимых переменных.