
- •1.1 Найти на заданном графике функции значения предела (предела справа, предела слева) в заданной точке (на бесконечности) или пояснить, почему он не существует.
- •1.2 Пояснить на примере графика функции понятия предела слева, предела справа и предела на бесконечности. Цифры от балды!! Так даны в педивикии. Просто чтобы уяснить суть.
- •1.3 Пояснить понятия «бесконечно малая» и «бесконечно большая», проиллюстрировать это на графике.
- •Следствия
- •Доказательство следствия
- •Часть 2.
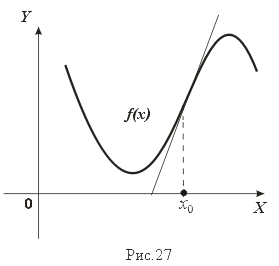
- •2.2 Геометрический смысл производной
- •2.3 Дать определение дифференциала, пояснить на графике понятия приращения и дифференциала.
- •2.4 Сформулировать теорему Лангранжа, пояснить геом. Смысл
- •2.5 Записать формулу Тейлора, пояснить ее геометрический смысл
- •2.6 В чем состоит правило Лопиталя
- •2.7 Пояснить, что такое min, max, inf, sup
- •2.8 Сформулировать, когда возможен экстремум функции.
- •Часть 3.
- •3.9 Записать 4 типа простейших дробей, взять интегралы
- •3.10 Дать определение неберущегося интеграла, и привести несколько примеров.
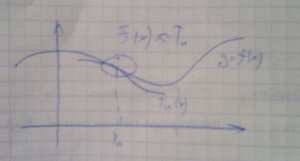
2.5 Записать формулу Тейлора, пояснить ее геометрический смысл
Смысл в том, что мы ищем максимально близкую к данной функцию.
Формула Тейлора показывает поведение функции в окрестности некоторой точки.
![]()
2.6 В чем состоит правило Лопиталя
Метод
нахождения пределов функций, раскрывающий
неопределённости вида
0 / 0 и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен пределу отношения
их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен пределу отношения
их производных.
Функции f(x) и g(x) удовлетворяют следующим условиям:
1. Существует f '(x) и g '(x) в окрестности точки хо
2.
![]()
![]()
3.
Существует ![]()
![]()
![]() Правило
Лопиталя.
Правило
Лопиталя.
2.7 Пояснить, что такое min, max, inf, sup
min, max - максимальное или минимальное значение функции.
inf- единственная точка минимума на отрезке
sup - единственная точка максимума на отрезке
2.8 Сформулировать, когда возможен экстремум функции.
Для непрерывной функции экстремум может иметь место только в тех точках, где производная или равна нулю ,или не существует (в частности, обращается в бесконечность).
Если точка xо является точкой экстремума функции f(x), то либо f '(xо) = 0, либо f '(xо) не существует. Такие точки называюткритическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
2.9 Что такое точка перегиба функции и как ее найти.
Точка перегиба функции - точка n(x0;y0), отделяющая выпуклую часть функции от вогнутой.
Точка перегиба - точка в которой меняется знак второй производной функции (производная второго порядка).
Чтобы найти точку перегиба нужно:
1. Найти вторую производную функции.
2.
Решить уравнение ![]()
3.
Найти промежутки на которых ![]()
4. Выбрать точки в которых меняется знак второй производной.
2.10 Пояснить на графике, что такое асимптота
Прямая линия называется асимптотой, если расстояние точки графика от асимптоты стремится к нулю при неограниченном удалении точки от начала координат (определение Осетрова)
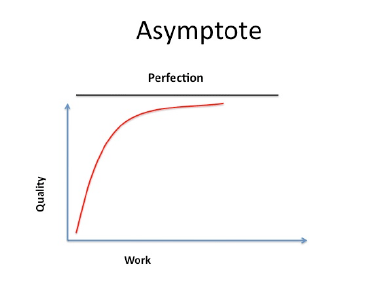
На слова не смотрите, красное- график, черное - асимптота.
Часть 3.
3.1 Дать определение первообразной функции.
Функцию, производная которой равна данной функции, называют первообразной для неё. (Нахождение первообразной определяется как операция, обратная к операции вычисления производной.)
Объяснение на примерах:
cos
x - производная sin x ![]() sin
x -первообразная cos x.
sin
x -первообразная cos x.
![]() -производная
ln |x|
-производная
ln |x| ![]() ln |x| - первообразная
ln |x| - первообразная
3.2 Неопределённый интеграл и его компоненты.
Семейство первообразных для f(x) на (а,в) называется неопределённым интегралом от функции f(x) и обозначается символом :
![]()
Знак ![]() называется интегралом,
называется интегралом,
![]() - подынтегральной
функцией
- подынтегральной
функцией
Если ![]() -одна
из первообразных для f(x),то согласно
сказанному:
-одна
из первообразных для f(x),то согласно
сказанному:
![]() ,
,
Где С- произвольная постоянная.
Неопределенный интеграл называется берущимся, если его можно выразить через конечное число элементарных функций и неберущимся в противном случае.
3.3 Пояснить в чём выражается линейность неопределенного интеграла,и как это может помочь при вычислении интегралов.
Линейность - это то, что любую функцию можно представить в виде линейной комбинации других функций.
Линейность интегрирования позволяет разбивать сложные интегралы на части.
![]() и
и 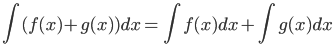
Cоответсвенно вытекает еще одно свойство как комбинация этих двух:
![]()
3.4 Таблица интегралов

3.5 Порядок вычисления методом замены переменной
Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением
![]()
где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.
3.6 Объяснить, как можно взять интеграл методом подведения под знак дифференциала
Метод
подведения под знак дифференциала
основан на равенстве ![]()
То есть, главной задачей является приведение подынтегральной функции к виду
![]()
Поэтому желательно иметь перед глазами таблицу производных основных элементарных функций.
Пример:
Вычислить
интеграл тангенса:
![]()
Решение:
![]()
Так как ![]() ,то
можно подвести под знак дифференциала
,то
можно подвести под знак дифференциала 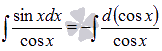 .Из
таблицы первообразных видим
.Из
таблицы первообразных видим  ,
где
,
где ![]()
Ответ:
![]()
3.7 Формула интегрирования по частям
Для неопределённого интеграла:
![]()
3.8 Ответить,всегда ли можно взять интеграл от целой, дробно-рациональной, рациональной, иррациональной,
трансцендентной функций.
Интеграл от целой функции всегда берётся.
Интеграл от дробно-иррациональной функции всегда берётся.
Интеграл от рациональной функции всегда берется.
Интеграл от иррациональной функции не всегда.
Интеграл от транцедентной функции не всегда .Например
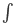 e(x2)
.
e(x2)
.
Элементарная функция, не являющаяся алгебраической называется трансцентной.
Другие интегралы удается взять лишь сделав замену переменной, чтобы функция по отношению к новой переменной стала рациональной.
Интеграл от правильной рациональной дроби, сведется к интегрированию простейших дробей.
