1.1 Найти на заданном графике функции значения предела (предела справа, предела слева) в заданной точке (на бесконечности) или пояснить, почему он не существует.
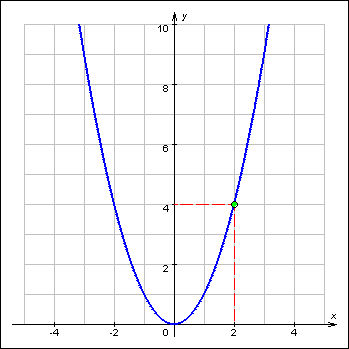
Предел
функции при 
равен 4.
Односторонний предел в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (пределом справа).
Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.
Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим. Существуют различные определения таких пределов, но они эквивалентны между собой.
Определение предела (на всякий случай) Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству
0 <| x-a |< ε, значения функции f(x) будут лежать в ε-окрестности числа А, т.е. |f(x)-A| < e.
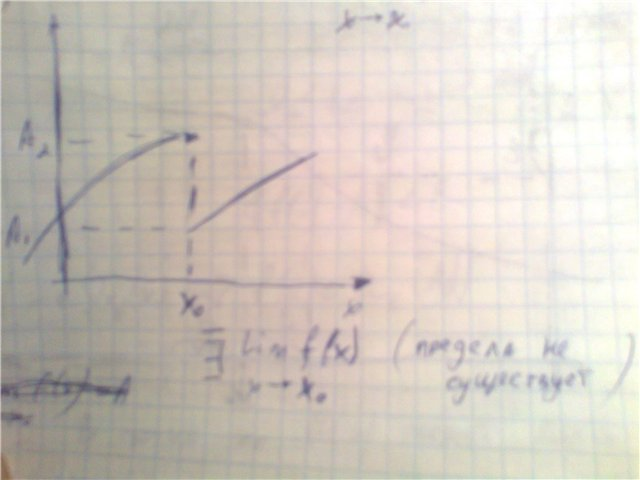
1.2 Пояснить на примере графика функции понятия предела слева, предела справа и предела на бесконечности. Цифры от балды!! Так даны в педивикии. Просто чтобы уяснить суть.
Предел
справа: 
7
Предел слева: 3
Обычного предела не существует.
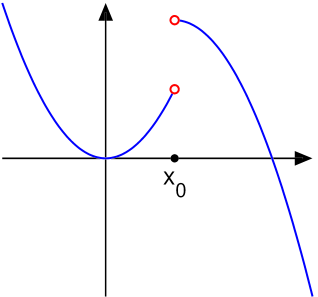
2) Функция, предел которой на бесконечности равен L.
Короче говоря, ели есть асимптота, то предел на бесконечности равен ей. В данном случае, прямая y=L является асимптотой, так то.
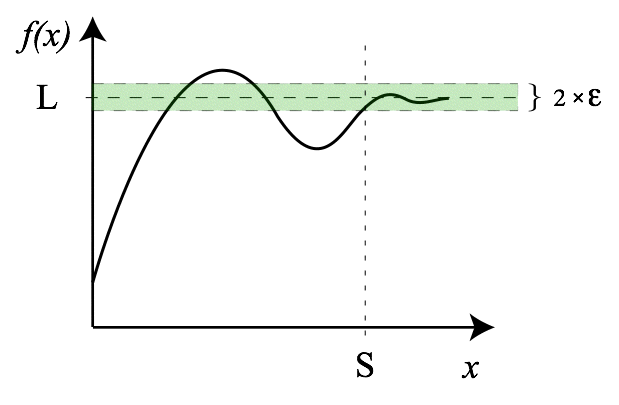
1.3 Пояснить понятия «бесконечно малая» и «бесконечно большая», проиллюстрировать это на графике.
Бесконечно малая-функция, предел которой равен нулю.
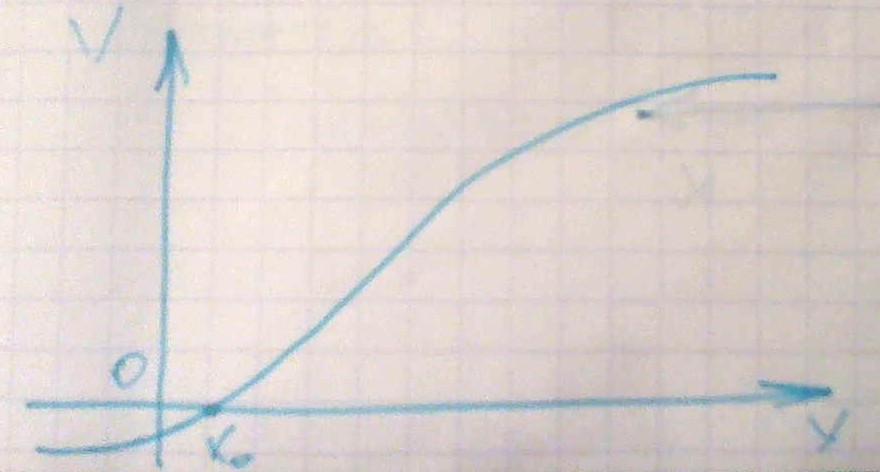
▲ Функция, бесконечно малая при x→x0
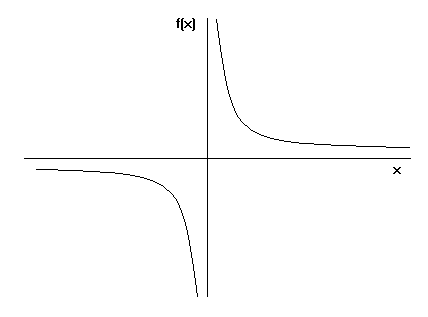
Функция
будет бесконечно малой при х стремящемся
к -
и
при х стремящемся к
Бесконечно большая- функция, предел которой равен бесконечности любого знака.
Например,
1)
f(x)= 
2) y=1/x^2
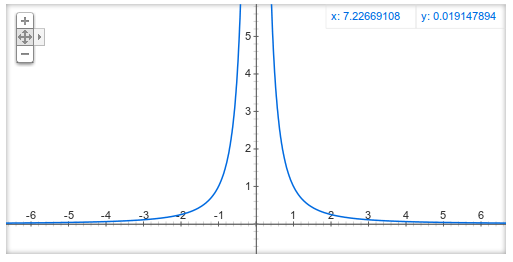
Если f(x) бесконечно большая при х→х0 ,то f(x)-не ограничена в окрестности точки хо. Обратное не верно.
1.4 Пояснить, какие бесконечно малые называются эквивалентными и привести несколько примеров.
Если 
,
то бесконечно малые величины α и β
называются эквивалентными
( 
.
Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.
1.5 Записать первый замечательный предел.
Первый замечательный предел:
1.6 Записать второй замечательный предел.
Второй замечательный предел:
-----------------------------------------------------------------------------------------
Следствия
Доказательство следствия
----------------------------------------------------------------------------------------------------------
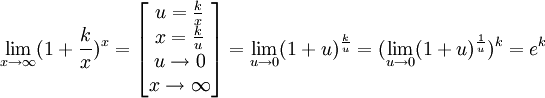
1.7 Виды неопределенностей :
|
|
|
|
|
|
|
1.8 Пояснить, как вычислить предел с помощью замены функций на их эквивалентные бесконечно малые.
Пределы отношения бесконечно малых можно упрощать, откидывая бесконечно малые слагаемые большего порядка и заменяя множители в числителе и знаменателе на эквивалентные бесконечно малые.
1.9 Дать определение функции, непрерывной в точке (через предел).
y=f(x)- непрерывна в точке хо по определению:
1) Данная функция должна быть определена в точке хо или в её окрестности.
2)
Существует 
.
3)
Предел не только существует, но и 
1.10 Определение функции, непрерывной на замкнутом промежутке
f(x)- непрерывна на [a;b]
1) f(x) непрерывна при любых х принадлежащих (a;b)
2) f(x) непрерывна справа в точке a
3) f(x) непрерывна слева в точке b