2.3. Звукопоглинання в житлових будівлях

Під звукопоглинанням розуміється процес перетворення енергії звукових хвиль у теплову енергію при поширенні звуку в середовищі або при падінні звуку на межу двох середовищ. У будівельній акустиці мова йде, в основному, про другій частині визначення процесу, а в якості кордонів двох середовищ найчастіше маються на увазі кордони «повітря-огороджувальні конструкції» приміщення.

Найбільш виразно процес звукопоглинання спостерігається в тих випадках, коли на кордоні з повітряним середовищем розміщують матеріали, у яких властивості перетворювати коливальну енергію звукової хвилі в теплову виражені найбільш яскраво. Ця група матеріалів (і виробів на їх основі) отримала назву звукопоглинальних.

Звукопоглинальні матеріали знаходять застосування в більшості сучасних засобів захисту від шуму. Вони входять до складу всіх відомих пристроїв для безпосереднього поглинання звуку акустичними облицюваннями огороджувальних конструкцій, для глушіння шуму, що поширюється в каналах вентиляційних систем, для ізоляції структурного звуку і вібрацій в якості пружних прокладок і покриттів, для поліпшення ізоляції звуку в якості заповнювача і ущільнювача щілин і отворів.

Основні види будівельних звукопоглинальних матеріалів та виробів

Класифікація матеріалів по структурним, сировинним і конструктивними ознаками

Ефективні звукопоглинальні матеріали поєднують структурні ознаки, протилежні одна одній. Звукопоглинальні матеріали повинні мати мінімальну щільність, максимальний обсяг наскрізних пор і максимальну питому площу поверхні пор.

Тому при розробці технології виробництва звукопогло ¬ щающая матеріалів виходять, насамперед, із структурних характе ¬ ристик: щільності, пористості, питомої площі поверхні пор. Варіюючи різними видами сировини та видозмінюючи технологічні режими, можна створювати матеріали певної структури, а отже, і властивостей.

Виходячи з цих вимог, всі відомі звукопоглинальні матеріали діляться по структурним ознаками на 4 типи:

- З волокнистою структурою;

- З зернистою структурою:

- Зі змішаною структурою;

- З комірчастою структурою.

Матеріали з волокнистою структурою, що володіють межволокністой пористістю, випускаються на основі мінеральної або скляної вати у вигляді напівфабрикатів (напівжорстких і жорстких плит, рулонів, матів), використовуваних як елементів звукопоглинальних конструкцій або у вигляді матеріалів повної заводської готовності (плити типу Спінтон).

Матеріали з зернистою структурою володіють тільки межгранульной пористістю, яка утворюється між зернами скелетооб-разователя - перліту, вермикуліту, шамоту, металу.

Випускають і пористу вогнетривку кераміку, що володіє також зернистою структурою, але використовувану в основному як теплову ізоляцію, тепловий захист або в якості гарячих фільтрів. Звукопоглинаючі властивості пористої кераміки невисокі (коефіцієнт звукопоглинання не перевищує 0,35-0,4 в середньому діапазоні частот, тому вона не знайшла застосування в будівельній акустиці.

Зернистою структурою володіє металокераміка, що отримується шляхом пресування металевих порошків (бронза, нержавіюча сталь, нікель) з додаванням наповнювача, в якості якого використовують парафін або 12%-ий водний розчин полівінілового спирту. При подальшому нагріванні спресованої суміші наповнювач випаровується, утворюючи пори між зернами металу.

За кордоном металокераміку застосовують у вигляді акустичних панелей. У вітчизняному виробництві освоєно випуск різних типів металокерамічних глушників шуму повітряного потоку, що випливає з пневматичних механізмів.

Матеріали зі змішаною структурою характеризуються наявністю як, внутрізерновой (внутрігранульной) пористості, так і міжзернової (межгранульной).

Матеріали з комірчастою структурою являють собою двофазну систему, що складається з скелетообразующего заповнювача і відносно рівномірно диспергованої газової фази.

Відомі полімерні і мінеральні матеріали з комірчастою структурою: пінополіуретан, вініпор, пеногипса, ніздрюватий бетон.

При цьому найбільше поширення одержали плити на основі пористого бетону автоклавного твердіння під умовною назвою «Сілакпор».

Перфоровані матеріали, використовувані як резолю ¬ нансних конструкцій, являють собою плоскі перфоровані пластини. Найбільшого поширення у нас в країні отримали перфорована суха гіпсова штукатурка, азбоцементні перфоровані плити, перфоровані металеві елементи з дюралюмінію.

По сировинних ознаками звукопоглинальні матеріали разде ¬ ляють на чотири групи:

- Матеріали мінерального походження (плити «Сілакпор», «Кермітон», пеногіпсовие, гіпсові і азбестоцементні перфоровані плити, мінераловатні плити і мати, які застосовуються як елементів звукопоглинальних конструкцій);

- Матеріали органічного походження (пінополіуретан, пінополіетилен, вініпор, полімерні плівки);

- Композиційні матеріали (плити Акмігран, Акмініт, Ар-МІТОН, Спінтон, Травертон, Акмінікс і т.д.),

- Матеріали з металу (дюралюмінієві, перфоровані екрани і профілі).

За конструктивними ознаками звукопоглинальні матеріали поділяються на п'ять груп:

- Звукопоглинальні вироби повної заводської готовності;

- Матеріали, що застосовуються в якості елементів конструкцій звукопоглинальних облицювань;

- Звукопоглинальні елементи плоского й об'ємного типу;

- Елементи кулісного типу;

- Резонансні звукопоглинаючі конструкції.

Всі перераховані ознаки в основному стосуються суто технологічних характеристик матеріалів і виробів. Ці ознаки можуть бути використані при вирішенні рецептури виготовлення матеріалів і встановленні технологічних режимів їх випуску для отримання матеріалів із заданими звукопоглинальні властивості, якщо знайдено зв'язок технологічних та акустичних параметрів.

Поряд з перерахованими ознаками істотні і відмінності по коефіцієнту звукопоглинання а в певному діапазоні частот. Матеріали і вироби з ос> 0,8 в діапазоні низьких (100-250 Гц), середніх (315-1000 Гц) і високих (1250-5000 Гц) частот віднесені до першого класу звукопоглотітелей, що забезпечують максимальне зниження рівня звукового тиску. Для другого класу в тих же діапазонах частот а = 0,4 - ^ -0,8, а для третього а <0,4. Використання цього основного чисто акустичного ознаки дозволило серед різноманіття застосовуються зараз конструкцій звукопоглинальних облицювань виділити три основні групи, що охоплюють по суті всі види випускаються в нашій країні виробів і відрізняються специфічними ознаками як конструктивного, так і акустичного характеру. До першої групи звукопоглинальних елементів, що мають найбільше поширення і одержали назву плоских, з повним правом можна віднести елементи, виконані з матеріалів повної заводської готовності (плити типу Акмігран, Екофон, Акусто та ін), а також у вигляді знімних касет з перфорованих (металевих , азбестоцементних, гіпсових) покриттів зі звукопоглинальними шарами з ультратонкого скляного й базальтового волокна або мінераловатних плит різних модифікацій. Акустична ефективність конструктивних елементів цієї групи відносно невелика, оскільки їх коефіцієнти звукопоглинання, як правило, не перевищують 0,8 - 0,9, а з урахуванням обмеженості займаної ними площі в приміщенні забезпечуваний такий облицюванням середній коефіцієнт звукопоглинання в більшості випадків не перевищує 0.5.

Другу групу звукопоглинальних елементів складають так звані об'ємні звукопоглинальні елементи, відмітною рисою яких в першу чергу слід назвати підвищений (в порівнянні з плоскими елементами) на 50-70% коефіцієнт звукопоглинання за рахунок додаткового поглинання внаслідок дифракції звукових хвиль і за рахунок більш розвинутої поверхні. У третю групу входять звукопоглинальні елементи, що є по суті об'ємними елементами, два розміри яких значно перевершують третій. Ці елементи виділені в самостійну групу через виняткову простоту їхнього виготовлення і монтажу, економічності, задовільного зовнішнього вигляду, високих вогнестійких якостей і отримали назву елементів кулісного типу. Умовні коефіцієнти звукопоглинання системи поглиначів кулісного типу (приведені до 1м2 поверхні огорожі досягають 2-2,5, тобто елементи цього типу значно перевершують по своїй ефективності елементи пер виття групи.

9.2. Звукопоглинальні вироби і конструкції повної заводської готовності

До числа найбільш поширених звукопоглинальних виробів повної заводської готовності, що випускаються вітчизняною промисловістю, можуть бути віднесені мінераловатні плити на крохмальному сполучному. У залежності від ступеня переробки мінеральної вати, концентрації та в'язкості сполучного можуть бути отримані вироби різної структури і з різними якісними показниками. Акустичні параметри таких матеріалів істотним чином залежать від розвитку питомої площі поверхні пор, щільності, діаметра волокна і т.п. Коефіцієнти звукопоглинання найбільш високі в області середніх і почасти високих частот.

Звукопоглинальний матеріал з високими акустичними властивостями можна виготовити і з волокнистих матеріалів на синтетичних зв'язуючих шляхом, введення сполучного в структуру волокнистого килима, одержуваного зі скляної вати в камерах волокноосажде-ня. Плити типу Армстронг і Акусто мають оптимальну щільність 50-100 кг/м3 і гладко мінливі в залежності від частоти хвильові параметри, що забезпечує їм настільки ж гладке зростання зі збільшенням частоти коефіцієнта звукопоглинання. На низьких частотах позначається негативний вплив в'язкості повітря так як діаметри волокон не перевищують 6-8 мкм і утворені ними капіляри-пори досить вузькі.

До матеріалів повної заводської готовності відносяться і багато ¬ слойні плити, виконані на основі напівжорстких мінераловатних плит щільністю 80-100 кг/м3 в поєднанні з перфорованим гіпсовим покриттям, складовим єдине ціле з футляром, в якому розміщується шар порістоволокністого матеріалу. Крім того, між покриттям і шаром звукопоглотітеля, як правило, розташовується проміжний захисний шар з акустично прозорого матеріалу.

Матеріали, які застосовуються в якості елементів конструкцій звукопоглинальних облицювань

Звукопоглинальні порістоволокністие матеріали складають основу всіх трьох груп елементів і в залежності від структури надають різну реакцію на падаючий на поверхню матеріалу звук. Ця реакція може бути оцінена за допомогою питомої акустичного імпедансу. Втрати звукової енергії в цих випадках відбуваються в силу ряду причин, головними з яких можуть бути названі ефекти в'язкості і теплопровідності повітря, а також податливості скелета матеріалу.

В'язке тертя при русі повітря у вузьких капілярах і обумовлює втрати звукової енергії всередині звукопоглинального матеріалу. До певної міри втрати можуть бути визначені опором продуванню повітря через шар матеріалу, в деяких випадках подчиняющемуся законом Пуазейля. Але оскільки процес стиснення повітря в порах матеріалу може протікати як адіабатичні, так і ізотермічно, то наявність теплопровідності може призвести до додаткових незворотних втрат енергії.

Явище податливості (або пружних коливань) скелета матеріалу також в ряді випадків призводить до незворотних втрат енергії релаксаційного характеру. У реальних звукопоглинальних матеріалах втрати можуть бути викликані однією з причин, але, як правило, в волокнистих структурах всі три механізми втрат беруть участь у процесі поглинання енергії падаючої хвилі.

В конструкціях звукопоглинаючих облицювань в якості звукопоглинального шару застосовують:

- Плити мінераловатні на синтетичному зв'язуючому, підлозі жорсткі, з діаметрами волокон 5-10 мкм, щільністю 50-100 кг/м3, вологостійкі, негорючі;

- Полотна з супертонкого скляного волокна діаметром не більше 3 мкм, щільністю 17-25 кг/м3, невлагостойкіе;

- Вироби з супертонких скляних волокон діаметром не більше 2 мкм, щільністю 7-15 кг/м3, облицьовані з одного або з двох сторін тканиною чи плівкою, важко горючі;

- Мати з супертонкого базальтового волокна вств щільністю 20-25 кг/м3, в захисній оболонці зі скляної тканини, негорючі, вологостійкі.

Оскільки основний елемент звукопоглощающей конструкції не має достатню міцність, його необхідно захищати оболонками і покриттями. В якості захисних оболонок застосовують:

- Скляну тканину, що представляє собою полотно різної щільності, що виробляється з кручених скляних ниток, негорючу, товщиною 70-100 мкм, з поверхневою щільністю не більш 0,11 кг/м2 марок А-1, ЕЗ-100, Е1-100, Е2- 100, а також скляну тканину завтовшки до 200 мкм з поверхневою щільністю до 0,2 кг/м2 марок ЕЗ-200, Т-23, ТСД;

- Павінол перфорований марки авіапол, негорючий матері ¬ ал зі скляної тканини з однобічним покриттям антіпірірован-ної полівінілхлоридної масою у вигляді смуг, що чергуються з про центом перфорації не менше 24, з поверхневою щільністю 0,25-0,57 кг/м2;

- Плівку поліетилентерефталатних ПЕТФ товщиною не більше 25 мкм, з поверхневою щільністю не більше 0,03 кг/м2.

В якості захисних покриттів використовують:

- Алюмінієві перфоровані панелі товщиною 0,8 мм, розміром 500x500 мм і коефіцієнтом перфорації 19% (ПАЗ 500/3-19);

- Алюмінієві перфоровані панелі товщиною 1 мм, розмірами 600 х 600 і 600 х 1200 мм з перфорацією по квадратній решітці і коефіцієнтами перфорації 14 і 16% відповідно (типу ЛАП);

- Алюмінієві перфоровані рейки товщиною 0,7 мм, раз заходами 100x3000 та 300x6000 мм з перфорацією по трикутнику і коефіцієнтом перфорації 23% (типу ЛАК);

- Плити гіпсокартонні штамповані, перфоровані з коефіцієнтом перфорації 9-12%, товщиною 10 мм, розмірами 500x500 і 500х 1000 мм з подклеенной з тильного боку тканиною або папером, важкогорючі;

- Просечновитяжние листи з алюмінію або сталі товщиною не більше 1,2 мм з розмірами вічок 30х 12, 26х 11, 24х 10 мм і з коефіцієнтом перфорації не менше 70%.

Всі захисні оболонки і покриття роблять вплив на акустичні властивості звукопоглинального шару. Тому можливість їх застосування повинна бути попередньо перевірена розрахунком по формулах або у відповідності з наявними рекомендаціями.

2.4. Акстика поглиначі та дифузерів

One of the most significant occurrences in the design of diffusers, if not the most important event, was the invention of the phase grating diffuser by Schroeder [1, 2]. Apart from very simple constructions, previous diffusers had not dispersed sound in a predictable manner. The Schroeder diffuser offered the possibility of producing so-called optimum diffusion and also required only a small number of simple to use design equations. D’Antonio and Konnert [3] presented one of the most readable reviews of the far field diffraction theory of Schroeder’s number theoretic surfaces, experimentally measured their performance and described their application in critical listening environments. Most crucially, they commercialized Schroeder diffusers and so made them widely available. Since the publication of Reference 3, there have been many new developments which have not been brought together and documented in one place. Therefore the intention of this chapter is to tell the whole story of Schroeder diffusers. Much of this chapter featured as a review article in the journal Building Acoustics [4].

The chapter will start by outlining a largely qualitative view of the diffuser, how it works and the basic design principles. Following this, a more detailed quantitative and theoretical analysis of the diffuser will be given. In these descriptions, the ingenuity of the original design concept will hopefully become apparent. In addition, more recent developments will be presented, illustrating weaknesses in the original design which can be overcome by modifying the design procedure, sometimes using one of Schroeder’s favourite subject area of number theory. Finally, it will be shown that better phase gratings can be made using an optimization procedure.

Basic principles

Figure 9.1 shows a single plane or 1D Schroeder diffuser. Itconsist s of a series of wells of the same width and different depths. The wells are separated by thin fins. The depths of the wells are determined by a mathematical sequence, such as the quadratic residue sequence. Single plane diffusers cause scattering in one plane, in the other direction, the extruded nature of the surface makes it behave like a plane surface. Because of this it is normal to just consider a cross section through the diffuser (Figure 9.2) which contains the plane of maximum dispersion. Multi-plane diffusers are possible as shown in Figure 9.1 and are discussed later in Section 9.7.

Consider a mid-frequency plane wave incident onto the diffuser. Plane wave propagation within the wells in the y-direction occurs. The plane waves are reflected from the bottom of the wells and eventually re-radiate into the space. For now, it will be assumed

Figure 9.1 Schroeder diffusers: single plane or 1D (left) and 2D (right).

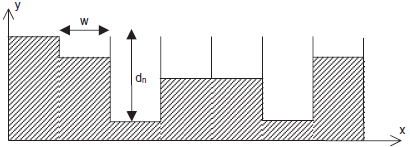
Figure 9.2 A cross section through an Nј7 quadratic residue diffuser QRD1). That there is no loss of energy. The pressure at a point external to the diffuser is therefore determined by the interference between the radiating waves from each well. All these waves have the same magnitude but a different phase because of the phase change due to the time it takes the acoustic wave to go down and up each well. Consequently, the polar distribution of the scattering is determined by the choice of well depths. Schroeder showed that by choosing a quadratic residue sequence, the energy scattered into each diffraction lobe direction is the same. In Figure 9.3, an example of the scattering from the surface is given, as calculated by the simplest and most approximate theory at a frequency where optimum diffusion is achieved. Eleven lobes of the same energy are found in this case. These lobes are generated because the surface is periodic.

Design equations

For the design theory to be correct, plane wave propagation within the wells must dominate. Consequently, an upper frequency for the diffusion to follow the simple design principles can be found from:

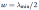
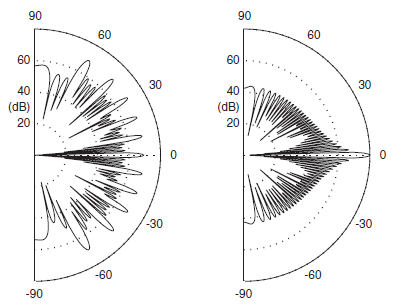
Figure 9.3 Scattered level from a Schroeder diffuser (left) and a plane surface (right) of the same size. where min is the minimum wavelength before cross modes in the wells appear and w the well width.

Above this limit scattering will continue to occur because these are complicated structures. Consequently, this is just a limit of applicability of a theory, and notan upper limiton the diffusion quality.

This need for plane wave propagation explains the need for fins to separate the different depth wells. Even for normal incidence, the lack of wells will cause the scattering not to follow these simple design principles. The fins should be as narrow as possible, but not so narrow that they vibrate and cause significant resonant losses.

A quadratic residue sequence is the most popular mathematical sequence used to form the well depths. The sequence number for the nth well, sn, is given by:

where modulo indicates the least non-negative remainder and is often written as mod for short. N is the prime number generator which in this case is also the number of wells per period. For example, one period of an N=7 QRD has

Schroeder diffusers work at integer multiples of a design frequency, f0. The design frequency is normally set as the lower frequency limit. It is more convenient to present formulations in terms of the corresponding design wavelength, λ 0, and so that will be done here. The depth of the nth well in the diffuser dn is determined from the sequence via the following equation:

The well depths consequently vary between 0 and approximately 0/2. The design frequency is not the lowest frequency at which the surface produces more scattering than a plane surface, it is just the first frequency at which the scattering can have even energy diffraction lobes. It has been shown that Schroeder diffusers scatter differently from a plane hard surface an octave or two below the design frequency [5, 6].

Some limitations and other considerations

Given the above equations, it is possible to design a diffuser to a desired bandwidth. There are some subtle details in the design that must be heeded to achieve the best possible diffusion.

If the period width (Nw) is too narrow, then at the first design frequency there is only one major lobe, and so this principle of even lobes is rather irrelevant. Theperiod or repeat width is often significant in determining performance, especially when the repeat width is small. This is illustrated in Figure 9.4 where the scattering from diffusers of different period widths is shown. These are both N=7 QRD

with a design frequency of 500Hz. The well widths are 3 and 9 cm, which means that the period widths are 21 and 70 cm respectively. The number of periods for each diffuser is set so that the overall widths of the devices are the same for a fair comparison. For the narrow wells and period width, shown right, the low frequency limit of diffusion is determined by the period width and not by the maximum depth.

This is illustrated in Figure 9.5 where the diffusion coefficient versus frequency is shown. The narrow well width diffuser only starts causing significant diffusion over and above the plane surface at 1.5 kHz, three times the design frequency.

This is roughly the frequency at which the first grating lobe appears for the narrow diffuser and so is the first frequency where significant scattering in oblique directions is achieved. For the wide well width, the first grating lobe appears below the design frequency and so significantdiffusio n is caused at 500 Hz and above.

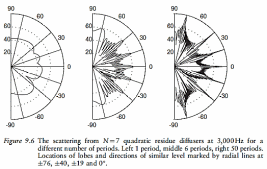
For the diffuser to behave optimally, the device must be periodic. The lobes are generated by the periodicity of the surface. Without periodicity, all that the design equations portray is the fact that in certain directions the scattering will have a similar level. This is illustrated in Figure 9.6 where the scattering from one and multiple periods of a diffuser is compared. The directions of similar level are marked. For the periodic cases, the directions of similar level align with the lobes. For the single period case, they are just points of identical level in the polar response; the points do not align with the lobes. Saying the levels are identical in this case is almost a meaningless statement, because in most polar responses there will be angles where the scattering is identical to other angles. Consequently, using one period of the device spoils the point of using the quadratic residue sequence. So using one period causes problems with the mathematical make-up and definition of optimum diffusion for a Schroeder diffuser. However, the scattering from a single period diffuser is often more uniform than a periodic device, as Figure 9.6 shows. This contradiction will be returned to later when modulation is discussed.

If too many periods are included then the grating lobes become rather narrow; this leads to uneven scattering because there are large nulls present, see Figure 9.6. It must be remembered, however, that manufacturing costs are likely to mean that a narrow base shape with a large number of repeats is going to be the cheapest build. Periodicity mightalso be preferred visually.

2.5. Вібродемпфування в будівлях

It is not practical to incorporate detailed microscopic representations of damping in the dynamic analysis of systems. Instead, simplified models of damping that are representative of various types of energy dissipation are typically used. Consider a general n-degree-of-freedom mechanical system. Its motion can be represented by the vector x of n generalized coordinates, xi;

representing the independent motions of the inertia elements. For small displacements, linear spring elements can be assumed. The corresponding quations of motion may be expressed in the vector matrix form

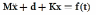
in which M is the mass (inertia) matrix and K is the stiffness matrix. The forcing function vector is f ðtÞ:

The damping force vector dðx; x_Þ is generally a nonlinear function of x and x_: The type of damping used in the system model may be represented by the nature of d that is employed in the system equations.

The various damping models that may be used, as discussed in the previous section, are listed in Table 1.1. Only the linear viscous damping term given in Table 1.1 is amenable to simplified mathematical analysis. In simplified dynamic models, other types of damping terms are usually replaced by an equivalent viscous damping term. Equivalent viscous damping is chosen so that its energy dissipation per cycle of oscillation is equal to that for the original damping. The resulting equations of motion are expressed by

In modal analysis of vibratory systems, the most commonly used model is proportional damping, where the damping matrix satisfies

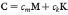
The first term on the right-hand side of Equation 1.29 is known as the inertial damping matrix. The corresponding damping force on each concentrated mass is proportional to its momentum. It represents the energy loss associated with a change in momentum (for example, during an impact). The second term is known as the stiffness damping matrix. The corresponding damping force is proportional to the rate of change of the local deformation forces at joints near the concentrated mass elements. Consequently, it represents a simplified form of linear structural damping. If damping is of the proportional type, it follows that the damped motion can be uncoupled into individual modes. This means that, if the damping model is of the proportional type, the damped system (as well as the undamped system) will possess real modes.