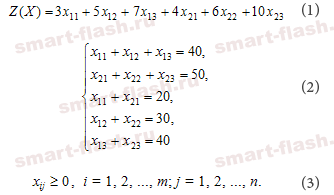Пример 2.8.3

По данным примера таблицы 2.16 найти оптимальный план при условии полного обеспечения потребностей пункта В3.

Таблица 2.16

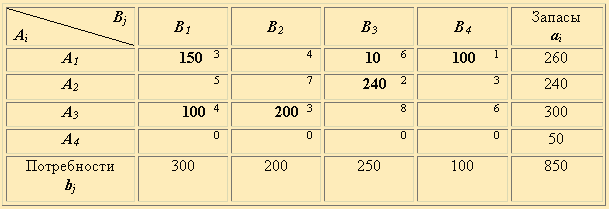
Следуя принципу минимальной стоимости, вносим в клетку А2 В3 груз 240 т. и недостающие 10 т. потребителю B3 заносим из A1. Исключаем из рассмотрения строку A2 и столбец B3 , уменьшая при этом a1 = 260 на 10 т. Решаем новую задачу (табл.2.16)

Таблица 2.17

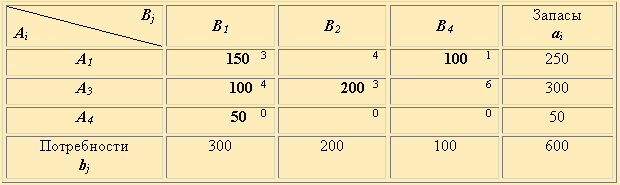
Проверяем оптимальность плана в табл. 2.16 методом потенциалов, и убеждаемся, что все ui+vj < cij в свободных ячейках. Находим Z1 = 1550. Добавив в матрицу, соответствующую последней таблице, строку A2 и столбец B3 из табл.3.18, находим решение задачи

и Zmin = 2090 (ед.).

В основном открытая модель транспортной задачи используется при решении ряда экономических задач.

Упражнения

Решить следующие транспортные задачи с дополнительными условиями (в ячейках таблицы даны тарифы cij, справа от таблицы - запасы ai, внизу ее - потребности bj ).

1.

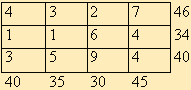
Полностью удовлетворить В2.

Заблокировать клетку А1В4.

2.

Из А3 в В4 доставить 20 ед. груза.

Вывезти полностью груз из А3.

3.

.

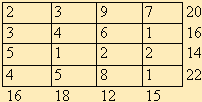Из А2 в В4 доставить не более 10 ед. груза.

4.

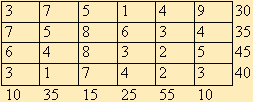
Из А2 в В5 доставить не менее 30 ед.

5. Пример составления математической модели транспортной задачи

Условие:

Однородный груз сосредоточен у m поставщиков в объемах a1, a2, ... am.

Данный груз необходимо доставить n потребителям в объемах b1, b2 ... bn.

Известны Cij , i=1,2,...m; j=1,2,...n - стоимости перевозки единиц груза от каждого i-го поставщика каждому j-му потребителю.

Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью, и суммарные затраты на перевозку всех грузов являются минимальными.

Исходные данные транспортной задачи записываются в виде таблицы:

Исходные данные задачи могут быть представлены в виде:

вектора А=(a1,a2,...,am) запасов поставщиков

вектора B=(b1,b2,...,bn) запросов потребителей

матрицы стоимостей:

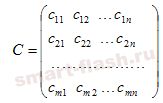
Математическая модель транспортной задачи

Переменными (неизвестными) транспортной задачи являются xij , i=1,2,...,m j=1,2,...,n - объемы перевозок от i-го поставщика каждому j-му потребителю.

Эти переменные могут быть записаны в виде матрицы перевозок:

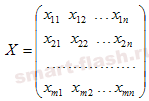
Так как произведение Cij*Xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны:

По условию задачи требуется обеспечить минимум суммарных затрат.

Следовательно, целевая функция задачи имеет вид:

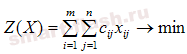
Система ограничений задачи состоит из двух групп уравнений.

Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью и имеет вид:

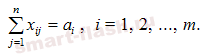
Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид:

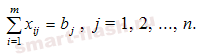
Учитывая условие неотрицательности объемов перевозок математическая модель выглядит следующим образом:

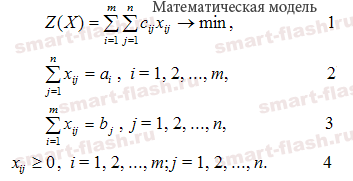
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.:

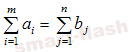
Такая задача называется задачей с правильным балансом, а модель задачи закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а модель задачи - открытой.

Математическая формулировка транспортной задачи такова: найти переменные задачи X=(xij), i=1,2,...,m; j=1,2,...,n, удовлетворяющие системе ограничений (цифра 2 на математической модели) , (3), условиям неотрицательности (4) и обеспечивающие минимум целевой функции (1)

Пример 34.1

Составить математическую модель транспортной задачи, исходные данные которой приведены в таблице 34.2

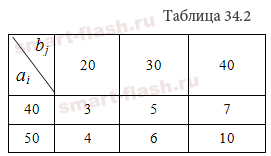
Решение:

1. Вводим переменные задачи (матрицу перевозок):

2. Записываем матрицу стоимостей:

3. Целевая функция задачи равняется сумме произведений всех соответствующих элементов матриц C и X.

Данная функция, определяющая суммарные затраты на все перевозки, должна достигать минимального значения.

4. Составим систему ограничений задачи.

Сумма всех перевозок, стоящих в первой строке матрицы X, должна равняться запасам первого поставщика, а сумма перевозок во второй строке матрицы X равняться запасам второго поставщика:

Это означает, что запасы поставщиков вывозятся полностью.

Суммы перевозок, стоящих в каждом столбце матрицы X, должны быть равны запросам соответствующих потребителей:

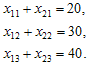Это означает, что запросы потребителей удовлетворяются полностью.

Необходимо также учитывать, что перевозки не могут быть отрицательными:

Ответ: Таким образом, математическая модель рассматриваемой задачи записывается следующим образом:

Найти переменные задачи, обеспечивающие минимум целевой функции (1) и удовлетворяющие системе ограничений (2) и условиям неотрицательности (3).