2.2 Сравнительный анализ матрицы частных коэффициентов корреляции с матрицей парных коэффициентов корреляции

Если переменные коррелируют друг с другом, то на величине парного коэффициента корреляции может сказываться влияние других переменных. В связи с этим возникает необходимость исследовать частную корреляцию между двумя переменными при исключении влияния остальных (m – 2) переменных.

Для получения матрицы частных коэффициентов корреляции в рабочем окне нажмите кнопку табличных опций и выберите Partial correlations (рисунок 12).

Рисунок 12 – Матрица частных коэффициентов корреляции

Проведём сравнительный анализ матрицы частных коэффициентов корреляции (рисунок 12) с матрицей парных коэффициентов корреляции (рисунок 11).

Сравнивая частные коэффициенты корреляции с соответствующими парными коэффициентами, видим, что за счёт «очищения связи» коэффициенты корреляции между у (объёмом реализации за квартал) и независимыми переменными х_i подверглись изменению, связь между у и х₁, у и х₃ ослабла, теснота связи между у и х₂ существенно не изменилась_. Следовательно, переменные х₂ и , х₂ и соответственно усиливали влияние факторов и на переменную , а переменные и не оказывали существенного влияния на тесноту связи между и .

Т.к. , то по силе влияния на переменную порядок факторов таков , , х_2.

3. Регрессионный анализ

Рассчитаем уравнения множественной регрессии y(х₁,х₂,х₃), y(х₁,х₃), y(х₂, х₃), y(х₁, х₂).

В строке меню основного окна выберем команду Relate, на экране появится список методов регрессионного анализа (рисунок 13).

Рисунок 13 – Список методов регрессионного анализа

• простая регрессия,

• полиномиальная регрессия,

• бокса-кокса преобразование,

• множественная линейная регрессия.

Выберем множественную регрессию (Multiple Regression). На экране появится диалоговое окно для ввода данных в процедуру построения моделей множественной регрессии. Выделим переменную Y нажатием левой кнопки мыши, затем введём её в поле Dependent Variable (зависимая переменная), аналогично переменные х₁, х₂, х₃ заносим в поле Independent Variables (независимые переменные) (рисунок 14).

Рисунок 14 – Окно диалога для ввода данных в процедуру построения моделей множественной регрессии

После нажатия кнопки ОК получим сводку проведённого анализа (рисунок 15).

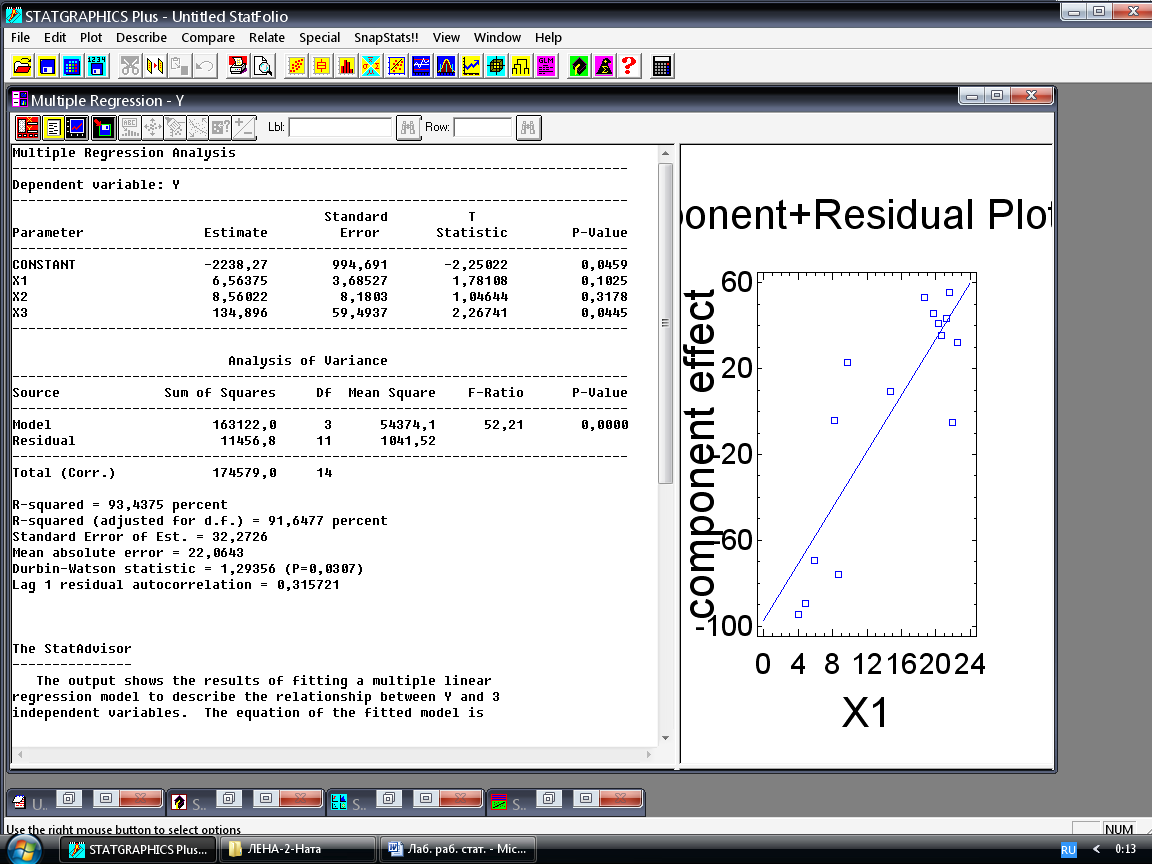
Рисунок 15 – Отчёт о множественной регрессии y (х₁, х₂, х₃)

Отчёт о множественной регрессии содержит следующую информацию: в столбце Estimate (оценка) приведены оценки параметров уравнения регрессии, т.е. рассчитаны свободный член и коэффициенты регрессии; столбец Standard Error содержит стандартные ошибки соответствующих оценок; столбец T Statistic ─ расчётные статистики Стьюдента; столбец P-Value ─ выборочный уровень значимости для соответствующих статистик Стьюдента. В таблице дисперсионного анализа Analysis of Variance рассчитаны суммы квадратов отклонений Sum of Squares, обусловленные регрессионной зависимостью (SSR) и случайными ошибками (SSE), соответствующие им числа степеней свободы Df, средние квадраты или оценки дисперсий Mean Square (MSR и MSE), значение критерия Фишера F-Ratio и значение уровня значимости P-Value для статистики Фишера.

Далее приведены:

R-Squared – коэффициент множественной детерминации,

R-Squared (adjusted for d. f.) – исправленный коэффициент множественной детерминации,

Standard Error of Est. – стандартная ошибка оценки,

Mean absolute error – средняя абсолютная ошибка,

Durbin-Watson Statistic – статистика Дарбина –Уотсона.

Аналогично рассмотренной выше процедуре получите отчёт о множественной регрессии y(х₁, х₃ ) (рисунок 16), y(х₂, х₃) (рисунок 17) ), y(х₁, х₂) (рисунок 18).

Рисунок 16 – Отчёт о множественной регрессии y(х₁, х₃ )

Рисунок 17 – Отчёт о множественной регрессии y(х₂, х₃ )

Рисунок 18 – Отчёт о множественной регрессии y(х₁, х₂ )

Рассчитаем уравнения парной регрессии y(х₁) , y(х₂), y(х₂), воспользовавшись процедурой построения простой регрессии: Relate/Simple Regression.

Рисунок 19 – Окно диалога для ввода данных в процедуру построения простой регрессии

В появившемся окне диалога (рисунок 19) выделим сначала переменную y и введём её в поле анализа Y нажатием кнопки со стрелкой, а затем переменную х₁ в поле анализа X. После нажатия ОК на экране появится отчёт о парной линейной регрессии y(х₁) (рисунок 20), y(х₂) (рисунок 21), y(х₃) (рисунок 22).

Рисунок 20 – Отчёт о простой линейной регрессии y(х₁)

Рисунок 21 – Отчёт о простой линейной регрессии y(х₂)

Рисунок 22 – Отчёт о простой линейной модели y(х₃)

Выпишем уравнения множественной и парной регрессий в натуральном масштабе (см. рисунок 16,17,18,20,21,22):

= – 2 238,27 + 6,56х₁ + 8,56х₂ + 134,896х₃,

= – 2 286,7+6,246 82х₁+145,414х₃,

= – 3 898,64 + 7,363х₂ + 234,599х₃,

= – 0,445 08 + 14,426 1х₁ + 11,693 7х₂,

= 176,805 + 14,843х₁,

= – 122,601 + 33,140 8х₂,

= – 3 871,17 + 239,54 х₃.

Рассмотрим выполнение пунктов 3.1 – 3.5 на примере анализа уравнения множественной регрессии y(х₁, х₃ ):

3.1. = b₀ + b₁x₁ + b₃x₃

Уравнение множественной регрессии y(х₁, х₃ ) имеет следующий вид:

= – 2 284,42+6,215 42х₁+145,323х₃.

Коэффициенты регрессии b₁ и b₃ показывают, что с увеличением x₁ и x₃ на единицу объём реализации продукции за квартал у в среднем соответственно увеличится на 6,215 42 и на 145,323 млн руб. Сравнивать эти значения не следует, т.к. они зависят от единиц измерения каждого фактора и поэтому несопоставимы между собой. Сопоставимость коэффициентов уравнения регрессии достигается при рассмотрении стандартизированного уравнения регрессии.

Оценим точность уравнения регрессии = – 2 284,42+6,215 42х₁+ 145,323х₃.

Определим значимость уравнения в целом, для чего воспользуемся процедурой дисперсионного анализа.

Проверим гипотезу Н₀: (все коэффициенты регрессии уравнения равны 0), при альтернативной гипотезе Н₁: хотя бы один 0 .

Для проверки гипотезы используется критерий Фишера

.

Табличное значение критерия определяется по таблице значений критических точек распределения Фишера – Снедекора (приложение Г), где ₁= ( m – число факторов в модели) и ₂= число степеней свободы для различных оценок дисперсии. Если расчетное значение F > , то Н₀ отвергается, в противном случае она не отвергается.

Т.к. расчётное значение критерия Фишера (см. рисунок 20) F = 77,54 больше табличного F_(0,05,2,12) = 3,885, гипотеза Н₀ о незначимости уравнения регрессии отвергается, принимается гипотеза Н₁: данное уравнение регрессии значимо.

Оценка значимости коэффициентов регрессии и свободного члена осуществляется с помощью t-критерия Стьюдента.

Выдвигаем гипотезу Н₀: =0 и альтернативную ей гипотезу Н₁: 0

Рассчитаем t-статистики по формулам:

для коэффициентов регрессии , где – стандартные ошибки коэффициентов регрессии;

для свободного члена , где – стандартная ошибка свободного члена.

Сравним полученное расчётное значение статистики t с табличным значением , которое определяется по таблице критических точек распределения Стьюдента (приложение Б) с  = ( ) степенями свободы ( – число единиц совокупности, – число факторов в уравнении) и заданным уровнем значимости (для двусторонней критической области). Если , то гипотеза Н₀ отвергается, коэффициент регрессии значим, в противном случае он не значим. Табличное значение статистики Стьюдента . Выясним, какие из коэффициентов регрессии равны нулю, а какие значимо отличны от нуля:

> , гипотеза Н₀: В₀=0 отвергается, принимается Н₁: В₀ 0;

< , гипотеза Н₀: =0 не отвергается;

> , гипотеза Н₀: =0 отвергается, принимается Н₁: 0.