1. Описательные статистики

1.1 По выборочным данным рассчитаем основные точечные оценки параметров генеральной совокупности и коэффициенты вариации

Будем использовать обозначения параметров генеральной совокупности, их оценок и характеристик выборочной совокупности, принятые в пособии “Статистические методы принятия решений” (П. Я Бушин, 2002 г.).

Характеристика	Параметр	Оценка	Выборочное значение
Средняя	μ
Дисперсия	σ 2	2	S2
Среднее квадратическое отклонение	σ		S

Для получения описательных статистик выберем Describe / Numeric Data / Multiple – Variable Analysis, появится окно для задания анализируемых переменных (рисунок 4).

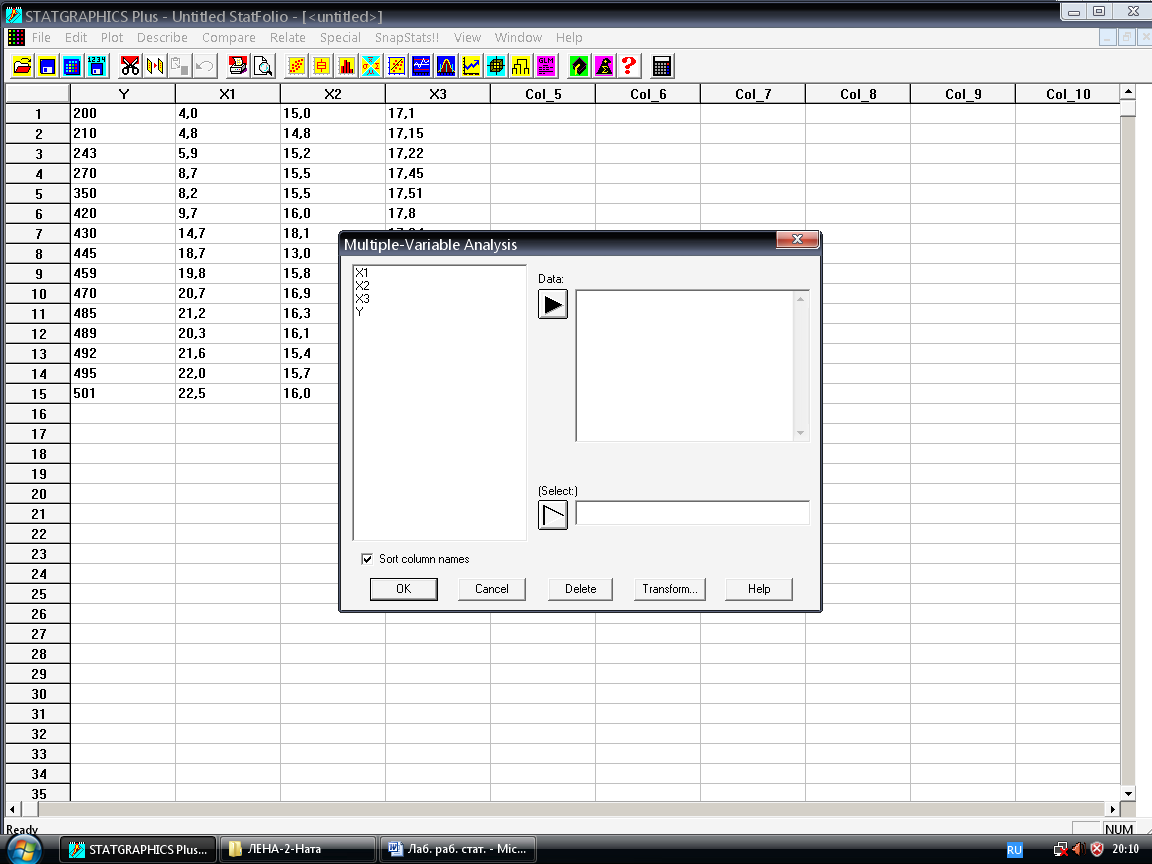
Рисунок 4 – Окно для задания анализируемых переменных

Введём в поле Data переменные х₁, х₂, х₃, у, для чего выделим указанные переменные нажатием левой кнопки мыши, затем кнопки Data и ОК.

По умолчанию на экране появится окно Multiple – Variable Analysis (рисунок 5), в котором представлена информация о том, что к анализу приняты переменные х₁, х₂, х₃, у, матрица парных коэффициентов корреляции и ее графическое изображение.

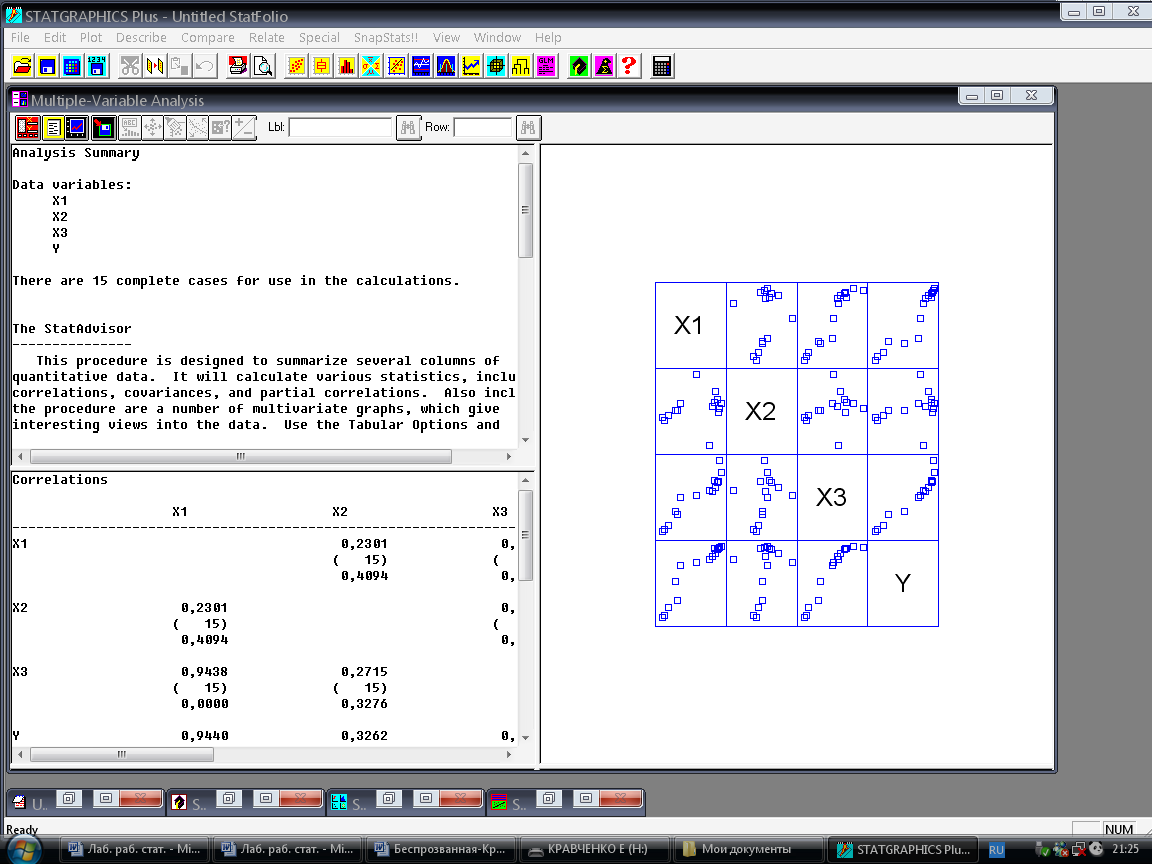
Рисунок 5 – Окно Multiple – Variable Analysis

Данное окно имеет свою кнопочную панель, расположенную под названием Multiple – Variable Analysis. Чаще используют первые четыре пиктограммы (слева направо), их назначения таковы: первая кнопка вызывает входную панель процедуры; с помощью второй пользователь устанавливает табличные опции; третья кнопка управляет графическими опциями; четвёртая даёт возможность сохранить результаты анализа в электронной таблице. Остальные восемь кнопок управляют графиками.

Нажмите кнопку табличных опций (вторая слева), на экране появится окно (рисунок 6), в котором рассматриваются следующие опции: описательный анализ, описательные статистики, доверительные интервалы, корреляции, ранговые корреляции, ковариации, частные корреляции.

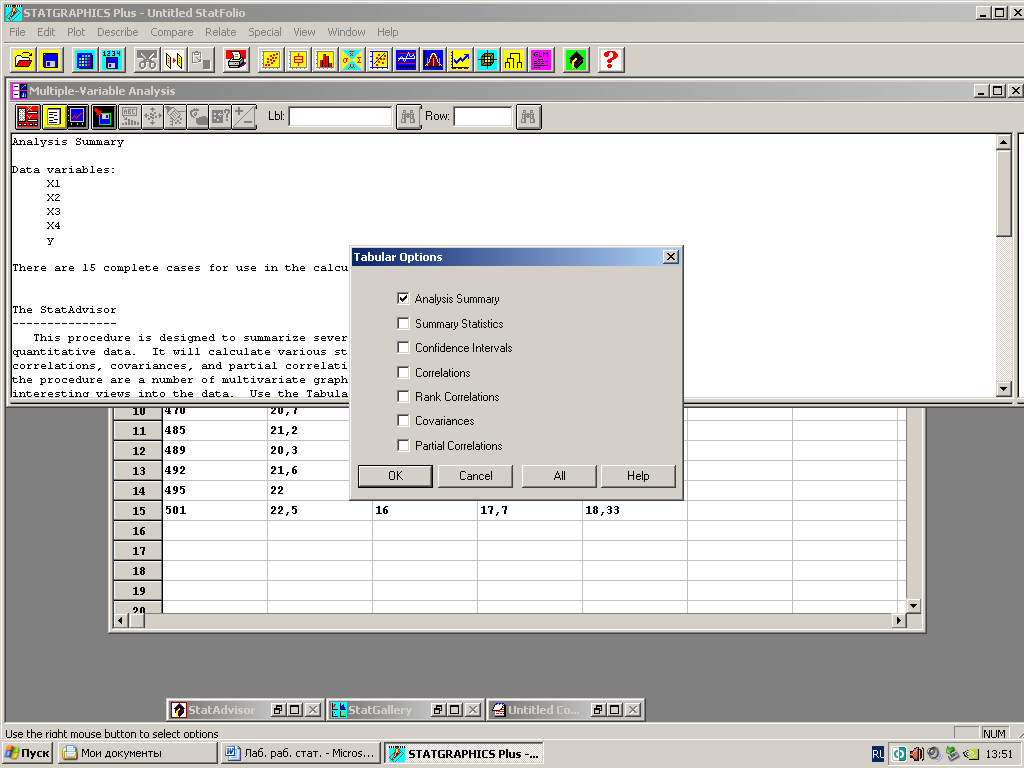
Рисунок 6 – Окно табличных опций

Выберите строку Summary statistics, затем нажмите кнопку ОК, по умолчанию на экране появится определённый набор статистик. Полный набор описательных статистик можно получить следующим образом: щёлкните правой кнопкой мыши, появится меню (рисунок 7).

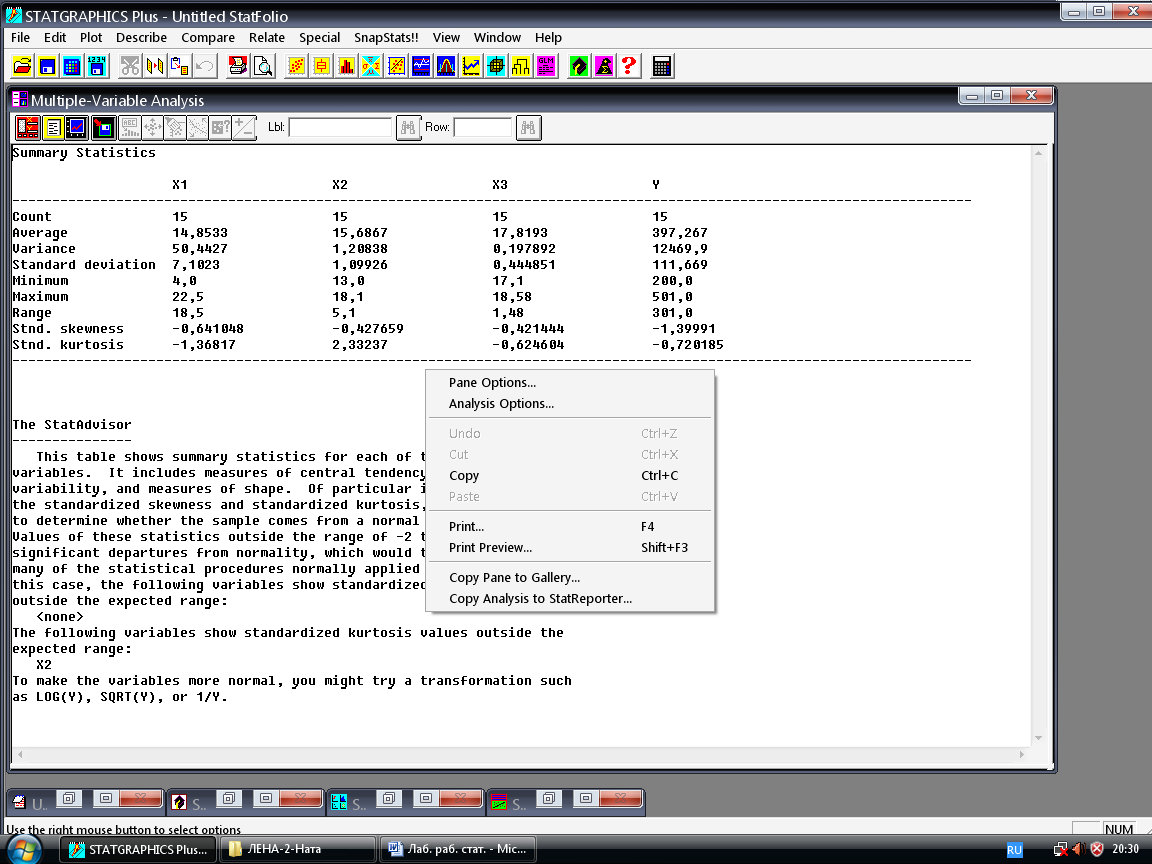
Рисунок 7 ─ Меню выбора команды

Выберите Pane Options, на экране появится окно Summary Statistics Options (рисунок 8), содержащее полный набор описательных статистик, в котором можно заказать необходимые изменения в наборе выдаваемых статистик.

Рисунок 8 – Окно опций описательных статистик

В таблице 1 приведена панель описательных статистик с их переводом.

Таблица 1 – Панель описательных статистик

Average ─ средняя	Min минимальное значение	Skewness асимметрия
Median ─ медиана	Max ─ максимальное значение	Std. Skewness ─ стандартная асимметрия
Mode ─ мода	Range ─ вариационный размах	Kurtosis ─ эксцесс
Geo. Mean ─ геометрическая средняя	Lower Quartile ─ нижний квартиль	Std. Kurtosis ─ стандартный эксцесс
Variance ─ дисперсия	Upper Quartile ─ верхний квартиль	Coeff. of Var. ─ коэффициент вариации
Std. Deviation ─ стандартное отклонение	Interquartile Range ─ межквартильный размах	Sum ─ сумма
Std. Error ─ стандартная ошибка

В окне Summary Statistics Options (рисунок 8) пометьте следующие статистики: average, variance, std. deviation, range , coeff. of var, sum. На экране появится отчет (рисунок 9) о значениях оценок заказанных статистик.

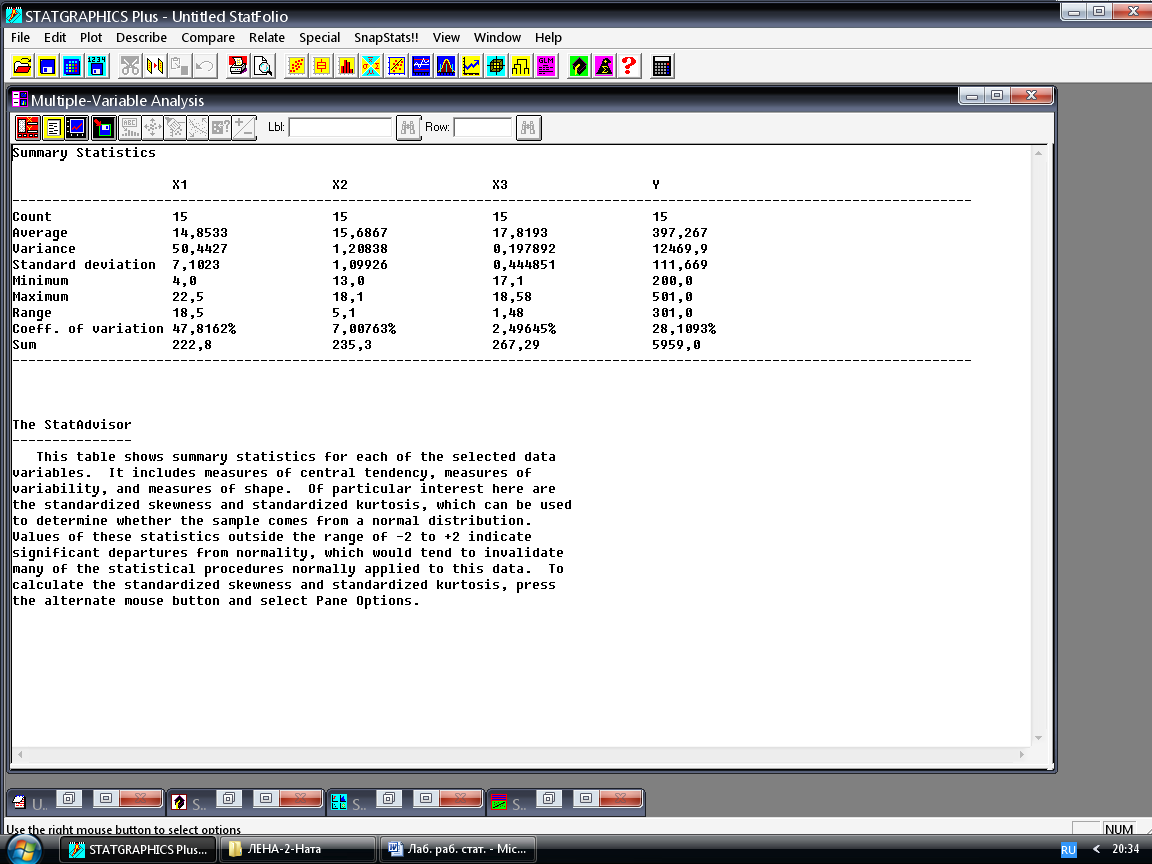
Рисунок 9 – Рассчитанные оценки описательных статистик

Для примера, рассчитаем точечные оценки для переменной x₁. Как известно, несмещённой, состоятельной и эффективной оценкой средней арифметической генеральной совокупности является выборочная средняя, т.е.

= =

= = = 14,8533

Несмещённой, состоятельной и эффективной оценкой дисперсии генеральной является исправленная выборочная дисперсия

² = S² = =

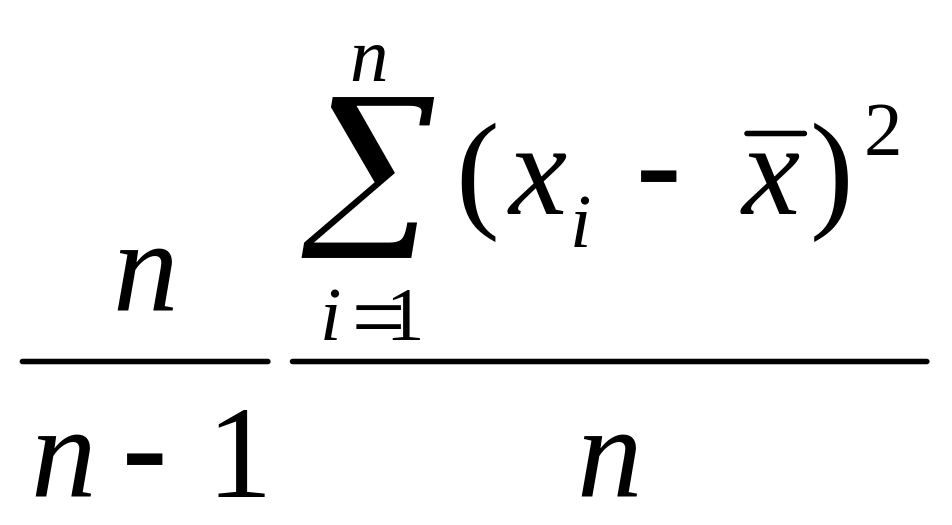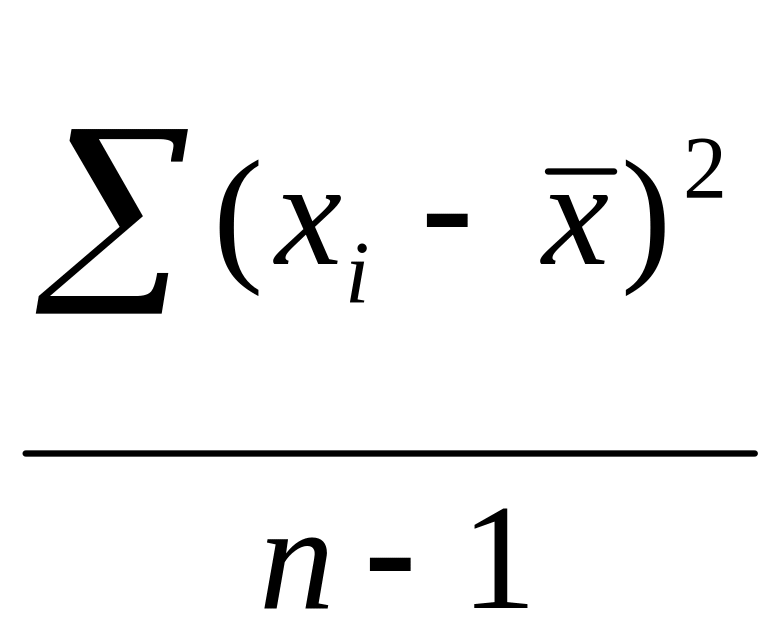
( (4  14,853)²+(4,8  14,853)²+(5,9  14,853)²+(8,7  14,853)² +(8,2  14,853)² + (9,7  14,853)² + (14,7  14,853)² + (18,7  14,853)² + (19,8  14,853)² + (20,7  14,853)² + (21,7  14,853)² + (20,3  14,853)² + (21,6  14,853)² + (22  14,853)² + (22,5  14,853)²) = =50,4427

Несмещённой, состоятельной и эффективной оценкой стандартного отклонения является

. =

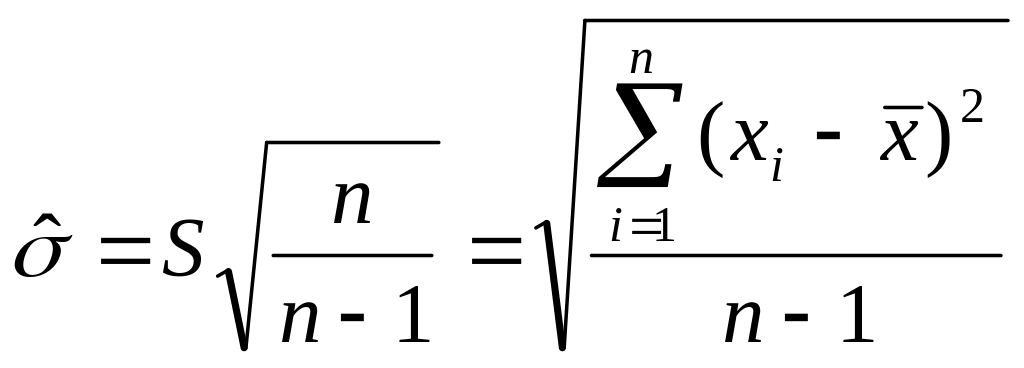Коэффициент вариации характеризует рассеяние значений совокупности вокруг среднего и находится по формуле

V= ; .

², и V являются мерами вариации и характеризуют меру рассеяния значений совокупности вокруг выборочной средней. ² и являются абсолютными показателями вариации; чем больше рассеяние данных вокруг средней, тем неоднороднее данная совокупность. Коэффициент вариации является относительной величиной, он не зависит от единиц измерения, поэтому используется для сравнительного анализа. Считается, что совокупность однородная, если V < 33 %.

Анализируя, полученные результаты, необходимо отметить, что наибольшее рассеяние значений вокруг выборочной средней присуще совокупности значений х_1, ( %), а наименьшее для совокупности значений x₃ ( %), при этом наибольшей дисперсией обладает совокупность значений у ( ).