Информация есть запомненный выбор одного варианта из нескольких возможных и равноправных. (q)

(G. Quastler)

Будем использовать это определение и ссылаться на него как на дефиницию (Q).

Определение (Q) отличается от предыдущих в следующем. Во-первых оно четко, понятно и широко используется в естественных науках. Конструктивность его проверена на многих примерах [25-28]. Это определение не противоречит предыдущим, когда речь идет о реальных задачах. Так, определение информации как инструкции или оператора в конкретных случаях сводится к указанию, какой именно выбор следует сделать в том или ином случае. Во-вторых согласно этому определению информация предстаёт как нечто конкретное и "приземленное", ощущение чего-то "сверхестественного и романтического в нем отсутствует, исчезает ореол "божественного". Можно считать это недостатком определения, поскольку именно это ощущение привлекает многих людей и вдохновляет их на подвиги (научные, не научные и лже-научные). Тем не менее, мы надеемся показать, что именно это определение позволяет понять такие тонкие явления как возникновение жизни и механизмы мышления с естественно-научной точки зрения. Иными словами - построить мост между естественными науками и гуманитарными. В-третьих определение (Q) допускает введение меры - количества информации.

Подчеркнем еще одну особенность определения (Q). Слово "выбор" - отглагольное существительное. Его можно понимать в двух смыслах: как процесс и как результат процесса. Разница примерно такая же, как между судопроизводством и приговором суда. В определении Кастлера выбор понимается, как результат процесса, но не как сам процесс. Именно в этом смысле (то есть как "приговор") оно конструктивно и именно в этом смысле оно используется в реальных задачах. Слово "процесс" в естественных науках прочно занято, оно означает изменение системы во времени (то есть "движение" её), которое в общем случае ещё не известно чем кончится и кончится ли вообще. Согласно определению (Q) при этом информация еще отсутствует. Однако, информация как результат выбора не мыслима без процесса выбора, как приговор не мыслим без суда. Отнюдь не любой процесс заканчивается выбором, Последнее возможно лишь в процессах определенного класса. Поэтому целесообразно ввести понятие "Информационный процесс", свойства которого мы обсудим позже.

В заключение этого раздела отметим, что в реальных задачах, как правило, фигурирует не просто информация, а ценная или осмысленная информация (пока мы употребляем эти термины, апеллируя к интуиции, определим их позже). Часто это упускают из внимания, полагая, что не ценная информация - вообще не информация. Последнее ведет к недоразумениям.

1.1.1. Количество информации

Эта величина была введена в 1948 году Клодом Шенноном [29] на примере текстового сообщения. Количество информации в сообщении, содержащем N символов I_N, по Шеннону равно;

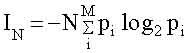
(1.1)

где M - число букв в алфавите, p_i - частота встречаемости i-ой буквы в языке, на котором написано сообщение, знак " - " перед всей правой частью формулы (1.2) поставлен для того, чтобы Ii была положительной, несмотря на то, что log₂ p_i < 0 (p_i < 1) . Двоичные логарифмы выбраны для удобства. При однократном бросании монеты М=2 ("орел" или "решка"), N = 1 и p_i =1/2. При этом получаем минимальное количеств информации (I=1), которое называется "бит". Иногда в (1.1) используются натуральные логарифмы. Тогда единица информации называется "нат" и связана с битом соотношением: 1 бит = 1,44 ната. Приведенные формулы позволили определять пропускную способность каналов связи, что послужило основанием для улучшения методов кодирования и декодирования сообщений, выбора помехоустойчивых кодов, словом, для разработки основ теории связи. В этом примере текст можно рассматривать как результат выбора определенного варианта расстановки букв. В общем случае, когда делается выбор одного варианта из n возможных (реализующихся с априорной вероятностью p_i: i=1,2,...,n), количество информации выражается формулой:

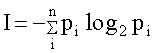i=1,2, ... n.

(1.2)

Если все варианты равновероятны, то есть p_i =1/n , то:

I= log₂ n .

В частном случае сообщения из N букв из бинарного алфавита (М=2) число вариантов равно: n = 2N , количество информации I= N, что совпадает с формулой (1.1). На этом примере удобно пояснить, что означает слово "равноправные" в определении (Q). Представим, что в тексте имеются символы, которые в алфавите вообще не содержатся (не "буквы"). Априорная вероятность такового считается очень малой ( p_n+1 << 1/n) и в сумме (1,2) не учитывается, поскольку он выпадает из рассматриваемого множества. Отметим, что формула (1.2) отражает количество информации, но не ценность её. Поясним это на примере. Количество информации в сообщении, определяемое формулой Шеннона, не зависит от того или иного сочетания букв: можно сделать сообщение бессмысленным, переставив буквы. В этом случае ценность информации исчезнет, а количество информации останется прежним. Из этого примера следует, что подменять определение информации (с учетом всех её качеств) определением количества информации нельзя. Исторически сложилось так, что определение количества информации было предложено раньше, чем определение самой информации. Для решения ряда практических задач это было полезно. Однако, в дальнейшем подмена понятий часто приводила к недоразумениям. Обсудим в связи с количеством информации ещё два понятия: "Информационная тара" (термин введен В.И. Корогодиным [23]) и "Информационная ёмкость". Первый связан с мощностью множества, из которого выбираются варианты. Второй используется для физических систем, способных хранить информацию. По смыслу они близки друг другу. Поясним смысл их на примере текста. Если любое сочетание букв в тексте является ценным, количество ценной информации совпадает с полным количеством, но не может превышать его. Это значит, что любая передача сигналов и/или запоминающее устройство может содержать какое-то количество ценной (или осмысленной) информации (не больше, чем (1.2) но может содержать и меньшее или не содержать вовсе. В этой связи количество информации в (1.2) можно назвать информационной тарой. Это понятие играет существенную роль при рецепции информации и/или при обработке её (в частности при перекодировке).

Приведем пример. Имеется текст на русском языке, содержащий N_r букв кирилицы (алфавит содержит 32 буквы). Перевод его на английский содержит N_a букв латинского алфавита (26 букв). Русский текст - результат выбора определенного варианта из Nr возможных (число вариантов порядка 32 в степени N_r ). Английский перевод - выбор определенного расположения латинских букв, который предопределен русским текстом (рецепция информации). Число вариантов в английском текста порядка 26 в степени N_a . Количество ценной информации одинаково (если смысл не искажен), а количество информации различно. Ниже, на примерах мы увидим, что процессы генерации, рецепции и обработки ценной информации сопровождаются "переливанием" информации из одной тары в другую. При этом, как правило. количество информации уменьшается, но количество ценной информации сохраняется. Иногда "информационные тары" столь различны. что можно говорить об информациях разного типа. Этот термин мы также будем применять к информациям, имеющим одинаковый смысл и ценность, но сильно различающихся количественно, то есть помещенных в разные тары. В заключение раздела отметим, что сам Шеннон не разделял понятия информация и количество информации, хотя и чувствовал. что это к добру не приведет. "Очень редко, - писал Шеннон, - удается открыть одновременно несколько тайн природы одним и тем же ключом. Здание нашего несколько искусственно созданного благополучия слишком легко может рухнуть, как только в один прекрасный день окажется, что при помощи нескольких магических слов, таких как информация, энтропия, избыточность... нельзя решить всех нерешенных проблем"[29].