Санкт-петербургский государственный политехнический университет
Инженерно-строительный факультет
Кафедра гидравлики
Задание №4 По курсу гидравлики
Выполнил Лазарева А.Ю.
3015/2
Преподаватель Зайцев О.И.
Санкт-Петербург
2012 г.
Содержание
Определить глубину равномерного движения
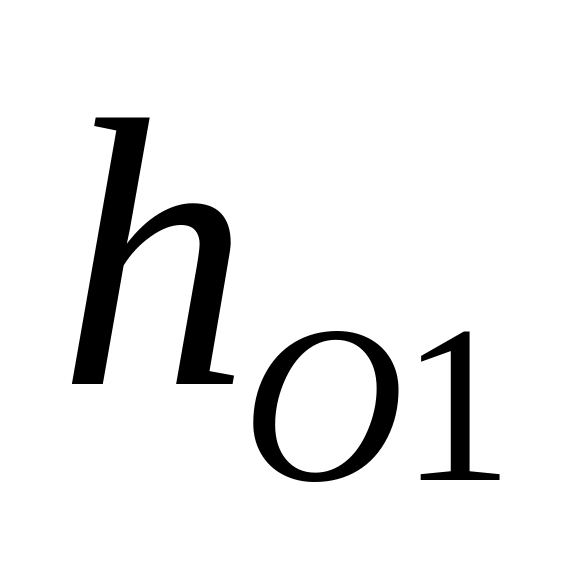и ширину канала по дну b
на подводящем участке канала при
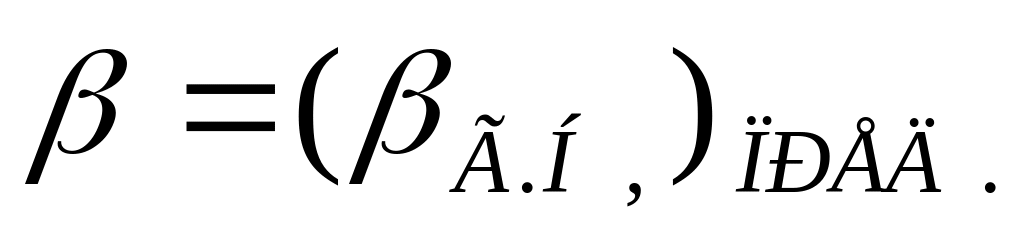.Определить глубину равномерного движения на отводящем участке канала
,
полагая ширину канала b, равной найденной
в пункте 1.Определить средние скорости движения воды в канале и сравнять их с максимально допустимыми для заданного грунта скоростями.
При
определить глубину наполнения и уклон
дна канала, полагая
.Определить критическую глубину
и критический уклон
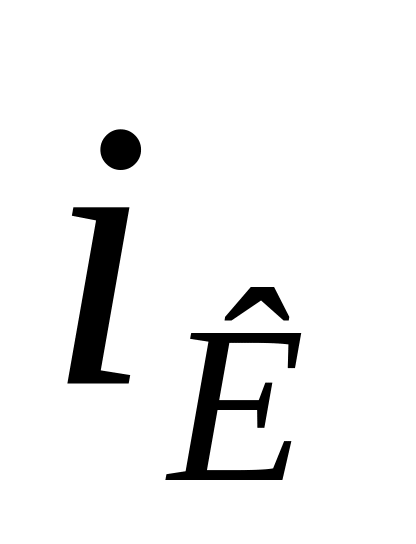.Построить график удельной энергии сечения Э(h).
Построить кривые свободной поверхности на отводящем участке канала при условиях: а) открытие затвора е= ; б) глубина воды в конце канала равна .
Построить график прыжковой функции
,
совместив его с графиком удельной
энергией сечения Э(h).Построить линия сопряженных глубин для кривой типа
и определить местоположение прыжка.Определить длину гидравлического прыжка и потери энергии в нем. Представить на рисунке схему гидравлического прыжка и показать на ней напорную линию.
Литература.
Определить глубину равномерного движения и ширину канала по дну b на подводящем участке канала при .
Таблица 1. Определение и b.
h, м |
b, м |
w,
|
|
R, м |
с,
|
Q,
|
1,5 |
6,19 |
16,59 |
16,39 |
1,01 |
55,67 |
22,77 |
1 |
4,13 |
7,38 |
10,93 |
0,68 |
52,03 |
7,72 |
0,95 |
3,92 |
6,66 |
10,38 |
0,64 |
51,59 |
6,74 |
0,87 |
3,59 |
5,58 |
9,50 |
0,59 |
50,84 |
5,33 |
,
м
Используя, то что мы
знаем значения Q,
,
n,
m,
,
найдем значения
и b.
Пример расчета:
Зная, что
,
h – глубина канала, b- ширина канала по
дну, а
,
где m- коэффициент откоса канала.
2,5+(3.25/2)=4.125(м);
b=1*4.125=4.125(м).
Вычислим площадь: w=(b+mh)h, w=(4.125+3.25*1)*1=7.38( ).
Вычислим смоченный
периметр:
=b+2h
,
=4.125+(2*1*(√1+3.252)=10.93(м).
Найдем гидравлический радиус: R=w/ , R=7.37/10.93=0,68(м).
Вычислим коэффициент
Шези:
,
n – коэффициент шероховатости,
с=6√0.68)/0.018=52.03(
).
Найдем расход воды в
канале:
,
где I- гидравлический уклон участка,
Q=7.38*52,0.3*√0.68*0.0006=7.72(
).
Сравнивая полученные значения Q при разных h с значением Q расхода воды в канале, заданным по условию, получим их примерное равенство при =0,87(м).
По результатам вычислений примем =0,87 (м).
Зная, что , то b=0,87*4.125=3,59(м).
Определить глубину равномерного движения на отводящем участке канала , полагая ширину канала b, равной найденной в пункте 1.
Таблица 2. Определение .
h, м |
b, м |
w, |
, м |
R, м |
с, |
Q, |
1 |
3,59 |
6,84 |
10,39 |
0,66 |
51,82 |
1,99 |
2 |
3,59 |
20,18 |
17,19 |
1,17 |
57,06 |
8,64 |
1,5 |
3,59 |
12,70 |
13,79 |
0,92 |
54,80 |
4,63 |
1,6 |
3,59 |
14,06 |
14,47 |
0,97 |
55,29 |
5,31 |
Используя, то что мы
знаем значения Q,
, n,
m,
b,
найдем значение
.
Вычислим площадь: w=(b+mh)h, w=(3.59+3.25*1)*1=6,84( ).
Вычислим смоченный периметр: =b+2h , =3,59+(2*1*(√1+3.252)=10.39(м).
Найдем гидравлический радиус: R=w/ , R=6,84/10.39=0,66(м).
Вычислим коэффициент Шези: , n – коэффициент шероховатости, с=6√0.66)/0.018=51.82 ( ).
Найдем расход воды в канале: , где I- гидравлический уклон участка, Q=6.84*51.82*√0.66*0.0006*0.08=1.99( ).
Сравнивая полученные значения Q при разных h с значением Q расхода воды в канале, заданным по условию, получим их примерное равенство при =1.6(м).
По результатам вычислений примем =1,6(м).