Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Башкирский государственный аграрный университет»

МАТЕМАТИКА

Методические указания и задания к выполнению расчетно-графической работы № 1 для всех направлений бакалавриата

Уфа 2012

00УДК 51(07)

ББК 22.1я73,22.161.6

М 54

Рекомендовано к изданию методической комиссией механического факультета (протокол № 9 от 27 июля 2012 года ) и заседанием кафедры математики (протокол № 7 от 10 апреля 2012 года)

Составитель: доцент Дик Е.Н.

Рецензент: доцент кафедры физики Юмагужин Р.Ю.

Ответственный за выпуск: зав. кафедрой математики доцент

Лукманов Р.Л.

Введение

Самостоятельная работа студентов является одной из составляющих учебного процесса. Способы ее организации совершенствуются и продолжают развиваться.

Методические указания представили классическую форму самостоятельной деятельности в виде вариантов расчетно-графической работы, позволяющих осуществить индивидуальную проверку знаний студентов, а также способствующих приобретению ими устойчивых навыков в решении задач по указанной теме. В настоящем сборнике представлено изучение раздела линейной алгебры. А именно, выбраны задания по темам: вычисление матричных многочленов и определителей, понятие минора и алгебраического дополнения, решение систем линейных алгебраических уравнений матричным методом, методом Крамера и методом Гаусса.

В методических указаниях приведены тридцать индивидуальных вариантов, каждый из которых содержит три задания и примеры решения типовых задач. Варианты заданий выдаются преподавателем. Приводится библиографический список, рекомендуемый для дополнительного изучения, имеющийся в наличии в библиотеке БГАУ.

Представляем решение некоторых типовых заданий.

Задача 1. Вычислить , где , ,

, , .

Решение. Выполним указанные операции с матрицами по действиям. Найдем сначала и :

;

.

Далее найдем сумму матриц и транспонируем ее:

;

.

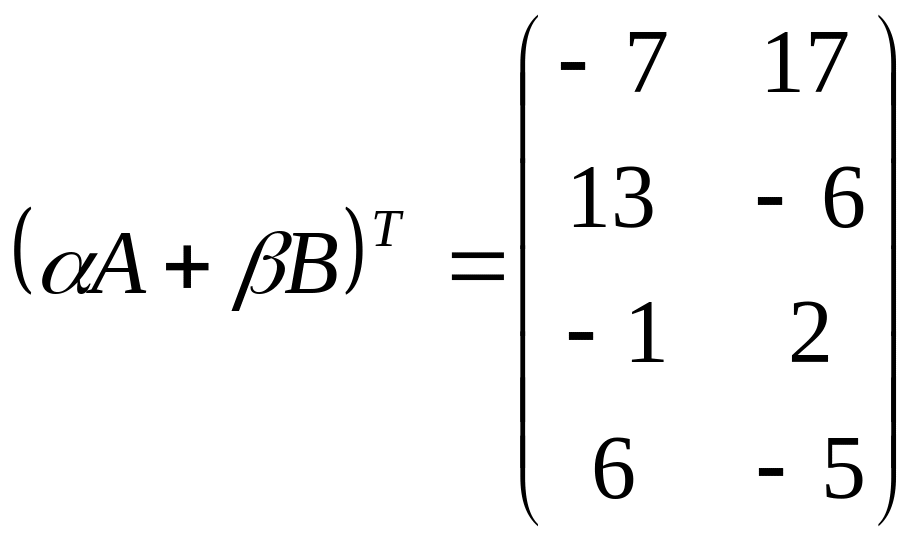Устанавливаем возможность выполнения действия умножения матриц. Первая матрица ( ) имеет порядок 4×2, вторая (C) - 2×3. Умножение возможно, поскольку число столбцов первой матрицы равно числу срок второй; в результате умножения получается матрица порядка 4×3. Следовательно,

= .

Ответ: .

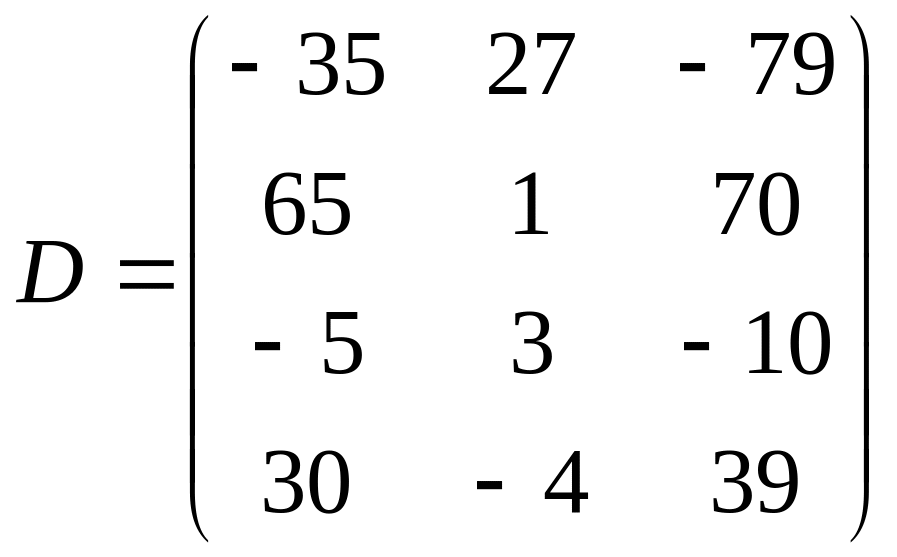Задача 2. Решить систему линейных уравнений методом последовательного исключения неизвестных. В случае неопределенности системы найти ее общее, базисное и любое частное решения.

1)

2)

Решение системы 1.

Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к ступенчатому виду.

Полагаем , , - свободные переменные. Из последней матрицы составим систему уравнений и выразим из нее базисные переменные.

- общее решение системы уравнений

Записываем несколько частных решений системы:

, , .

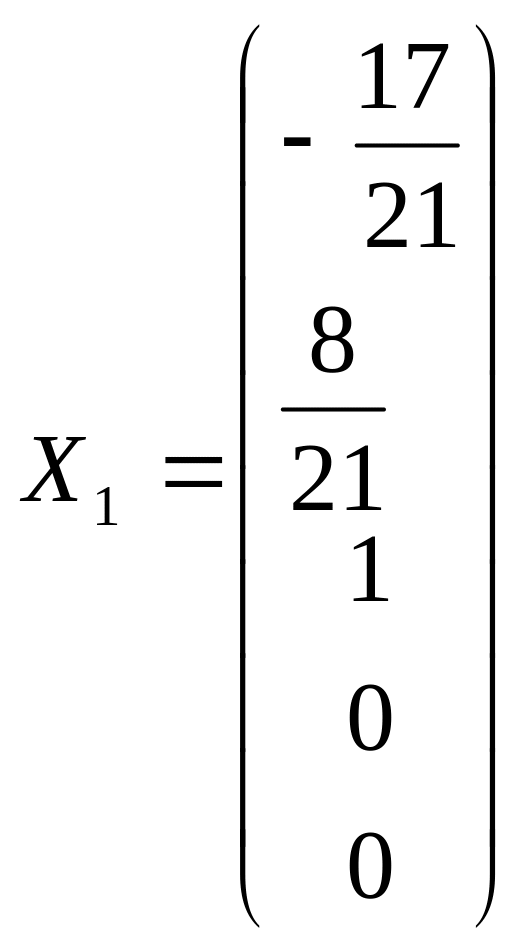Решение системы 2.

Выписываем матрицу системы и с помощью элементарных преобразований приводи ее к ступенчатому виду.

Полагаем , , тогда:

- общее решение системы уравнений

Придадим свободным переменным произвольные значения, получим частное решение, например, при :