1.2. Комплексная плоскость.

Понятие области на комплексной плоскости.

Понятие предела последовательности комплексных чисел

Р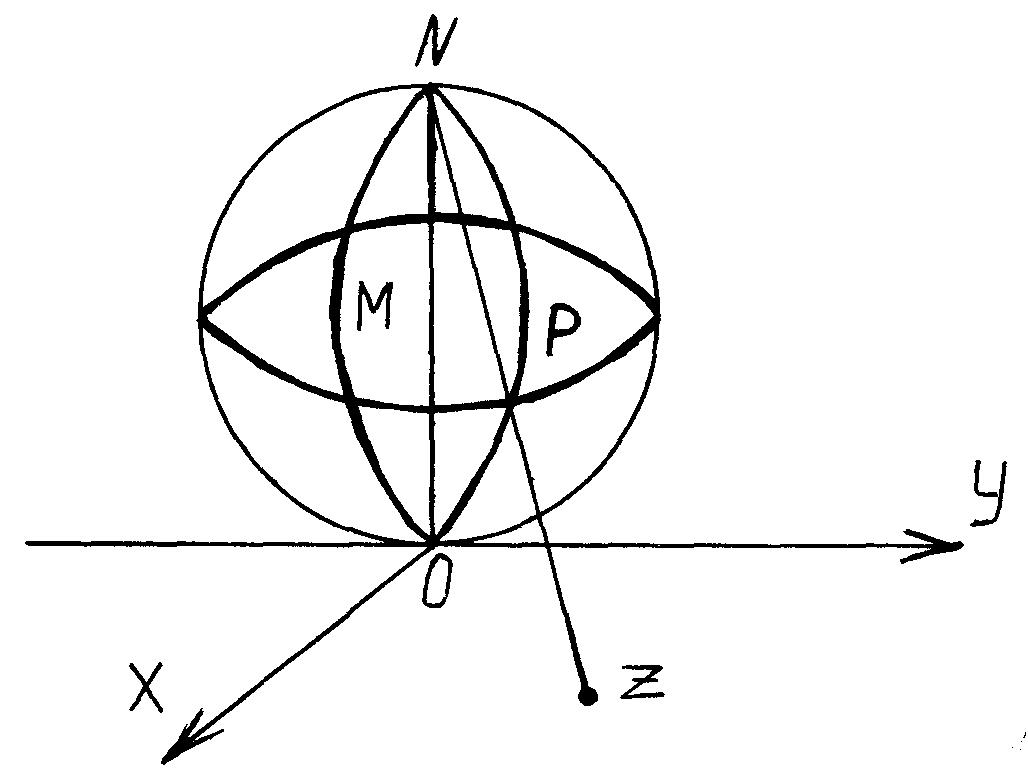 анее мы определили комплексную плоскость как плоскость XOY, которая служит для изображения комплексных чисел. Расширенной комплексной плоскостью называется плоскость XOY, дополненная

идеальной (воображаемой)

точкой z = , называемой

бесконечно удаленной точкой.

Чтобы лучше понять роль

этой точки, построим в прост-

ранстве OXYZ сферу с центром в

в точке M(0;0;1/2) радиуса R = 1/2 Рис.1.4

(рис.1.4). Любую точку z = x+iy соединим прямой с точкой N на сфере. Точка P пересечения этой прямой со сферой называется стереографической проекцией точки z на сферу.

Если z, то точка P приближается к точке N. Поэтому естественно считать точку N стереографической проекцией бесконечно удаленной точки. Роль точки z =  подобна роли точки N на сфере.

Окрестностью точки z₀ называется совокупность внутренних точек любого круга с центром в точке z₀ радиуса , то есть совокупность точек z, удовлетворяющих неравенству z-z₀ < .

Окрестностью бесконечно удаленной точки называется совокупность точек, лежащих вне любого круга с центром в начале координат, то есть множество точек, удовлетворяющих неравенству z > R.

Пусть E - множество точек комплексной плоскости. Точка z называется внутренней точкой множества E, если существует окрестность этой точки, принадлежащая множеству E. Точка z называется граничной точкой множества E, если любая окрестность этой точки содержит точки, принадлежащие множеству E, и точки, не принадлежащие этому множеству. Множество Г всех граничных точек множества E называется границей множества E.

Множество E называется открытым множеством, если оно состоит из одних внутренних точек. Множество E называется связным, если любые две точки этого множества можно соединить непрерывной кривой, состоящей из точек множества E. Всякое открытое связное множество D на комплексной плоскости называется областью. Область D называется односвязной, если любую замкнутую кривую в этой области можно непрерывно стянуть в точку, не пересекая границу области. В противном случае область D называется многосвязной.

На рис. 1.5 изображены односвязная область D и многосвязная область .

Множество, состоящее из точек области D и ее границы Г, называется замкнутой областью и обозначается D. Обход границы Г области D считается положительным, если при движении в этом направлении точки области D остаются слева.

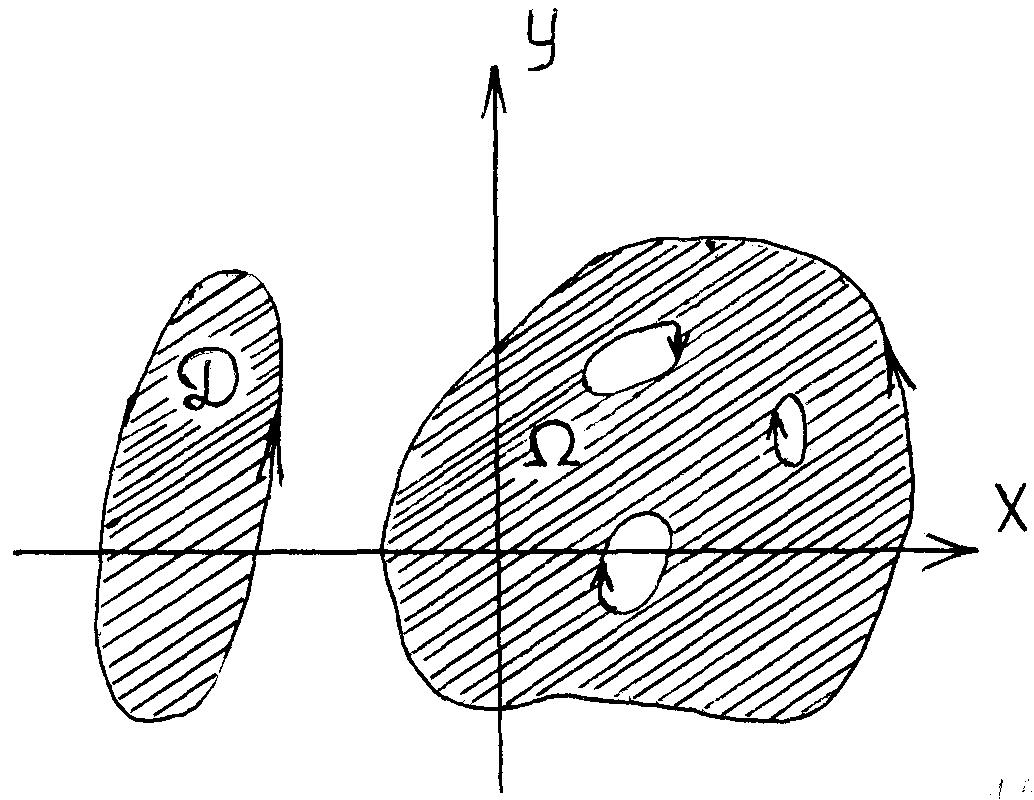
Рис. 1.5

Множество, состоящее из точек области D и ее границы Г, называется замкнутой областью и обозначается D. Обход границы Г области D считается положительным, если при движении в этом направлении точки области D остаются слева. На рис.1.5 положительное направление обхода границы Г отмечено стрелками.

Рассмотрим теперь последовательность комплексных чисел

z₁, z₂,...., z_n,....

Число z₀ называется пределом последовательности {z_n}, если для любой окрестности точки z₀ существует число N такое, что все числа z_n при n > N принадлежат этой окрестности. В этом случае пишут

.

Это определение справедливо и тогда, когда z₀= – бесконечно удаленная точка.

Последовательность {z_n} называется сходящейся, если предел z₀ этой последовательности – конечное число.

Пусть z_n = x_n+iy_n, z₀ = x₀+iy₀. Легко доказать, что если последовательность {z_n} имеет конечный предел z₀, то последовательности {x_n} и {y_n} имеют конечные пределы x₀ и y₀, и наоборот, если существуют конечные пределы

, ,

то

z_n = z₀ = x₀+iy₀.