1.1.2. Сложение и вычитание комплексных чисел
Сумма и разность комплексных чисел
z1=x1+iy1 и z2 = x2+iy2 определяются по формулам
z1+z2 = (x1+x2) + i(y1+y2),
z1-z2 = (x1-x2) + i(y1-y2).
О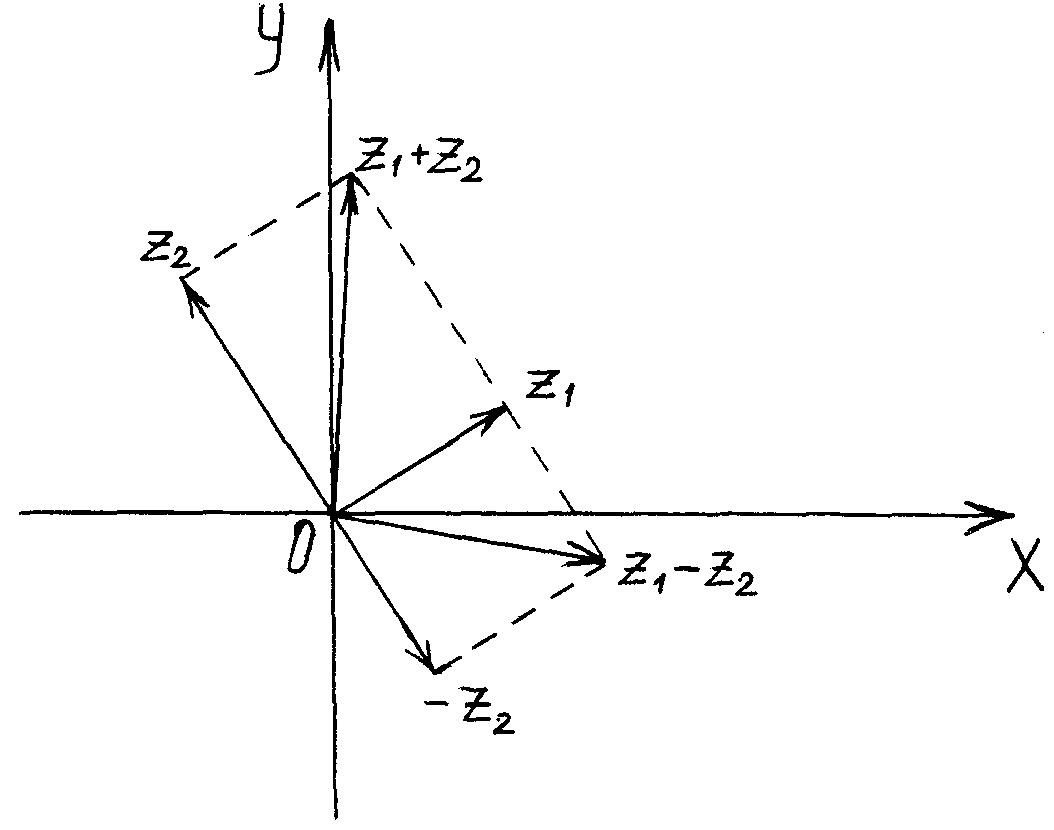
тсюда
следует, что действительная и мнимая
части суммы и
разности комплексных чисел определяются так же, как координаты суммы и разности соответствующих векторов на плоскости. При этом следует придерживаться правила: начало всех векторов помещать в начало координат (рис.1.2). В частности, из треугольников с вершинами в точках 0, z1, z1+z2 и
0, z1, z1-z2 следует, что Рис.1.2
z1z2 z1 + z2, z1z2 z1 - z2. (1.3)
1.1.3. Умножение и деление комплексных чисел
Умножение двух комплексных чисел z1=x1+iy1 и
z2=x2+iy2 производится по правилу умножения многочленов, при этом учитывается, что i2 = -1, i3 = -i, i4 = 1 и так далее
(x1+iy1)(x2+iy2) = (x1x2-y1y2) + i(x1y2+x2y1). (1.4)
Из формулы (1.4), в частности, следует, что произведение двух взаимно сопряженных комплексных чисел является действительным числом, равным квадрату модуля этих чисел
=(x+iy)(x-iy)
= x2+y2
= z2.
(1.5)
Сумма двух взаимно сопряженных чисел также является действительным числом
z+
=
(x+iy)
+ (x-iy)
= 2x
= 2Rez.
(1.6)
Деление комплексных чисел определяется как операция, обратная умножению: частным от деления числа z1 на число z2 называется число z такое, что z∙z2 = z1. Это равенство невозможно, если z2=0, а z10. Это означает, что деление на 0 невозможно.
Пусть z1=x1+iy1, z2=x2+iy20, z=x+iy. Тогда, в силу определения частного,
(x+iy) (x2+iy2)=x1+iy1
или
(x2x-y2y)+i(y2x+x2y)=x1+iy1.
Приравнивая действительную и мнимую части в этом равенстве, получим систему уравнений для определения x и y
Отсюда находим, что
.
Таким образом,
(1.7)
Этот же результат можно получить по-другому. Для этого нужно числитель и знаменатель дроби z1/z2 умножить на число, сопряженное к знаменателю, и произвести умножение чисел в числителе и в знаменателе.
Если комплексные числа z1 и z2 заданы в тригонометрической форме:
z1=r1(cos1+isin1), z2=r2(cos2+isin2),
то
z1z2=r1(cos1+isin1) r2(cos+isin)=
=r1r2 ((cos1 cos2-sinsin2)+i(sincos2+cos1sin2)=
=(r1r2)(cos(1+2)+isin(1+2). (1.8)
Отсюда следует, что модуль произведения комплексных чисел равен произведению модулей, а аргумент - сумме аргументов сомножителей.
Пусть теперь z1/z2 = z = r(cos + isin). Так как z2z=z1,
то, в силу (1.8), r2r=r1, 2+=1.
Отсюда следует, что r=r1/r2, =1-2:
z1/z2=(r1/r2)(cos(1-2)+isin(1-2)), (1.9)
то есть
z1/z2=z1/z2, Arg(z1/z2)=Argz1-Argz2.
1.1.4. Возведение комплексных чисел в целую
положительную степень. Формула Муавра.
Извлечение корня из комплексных чисел
Как и для действительных чисел, n-я степень комп-плексного числа z определяется как произведение n одинаковых множителей z
zn = z z z ... z.
n - множителей
Если число z задано в тригонометрической форме z=r(cos+isin), то, в силу (1.7 получаем
(r(cos+isin))n=rn(cosn+isinn): (1.10)
при возведении комплексного числа в n-ю степень его модуль возводится в n-ю степень, а аргумент умножается на n.
В частности, если r=1, то
(cos+isin)n=cosn+isinn. (1.11)
Соотношение (1.8) называется формулой Муавра. С помощью формулы Муавра легко решается следующая тригонометрическая задача. Выразить cosn и sinn через степени функций cos и sin .Например, при n=3 из формулы (1.11) следует, что
cos3+3icos2 sin-3cos sin2-isin3=cos3 + isin3.
Приравнивая в этом равенстве действительную и мнимую части, получаем
cos3 = cos3-3cossin2, sin3 = 3cos2 sin - sin3
Заметим, что формулы (1.10) и (1.11) справедливы и для целых отрицательных n. В самом деле, пусть N=-k (k>0). Тогда
[r(cos+isin)]n=1/[r(cos+isin)]k=1/[rk(cosk+isink)]=
=r-k[cos(-k)+isin(-k)]= rn(cosn+isinn).
Переходим
к операции извлечения корня из комплексных
чисел. Корнем n-й
степени из комплексного числа z
называется
комплексное число w, для которого
выполняется равенство wn=z.
Пусть число z0
задано в тригонометрической форме:
z=r(cos+isin),
и пусть число w=
=(cos+isin).
Из определения, корня n-й
степени из z
следует, что
((cos+isin))n=r(cos+isin)
или
n(cosn+isinn)=r(cos+isin).
Отсюда
следует, что n=r,
n=+2k,
где k
– любое целое число. Так как r
положительное число, то из первого
равенства следует, что =
,
где
- арифметический корень n-й
степени из числа r.
Из второго равенства находим, что
=(+2k)/n.
Таким образом, формула для извлечения корня n-й степени из комплексного z0 имеет вид
=
.
(1/12)
Придавая k значения 0,1,2,...., n-1, получим n различных значений корня n-й степени из числа z. Изображения этих значений на комплексной плоскости являются вершинами правильного n-угольника, вписанного в окружность радиуса , с центром в начале координат. Аргумент одной из вершин равен
/n. Все значения корня n-й степени из числа z=0 совпадают и равны 0.
Пример:
Найти все значения
.
В тригонометрической форме
-1=cos+isin, (-1=1, arg(-1)=).
По формуле (1.12) находим, что
w= =1(cos((+2k)/4)+isin((+2k)/4)), k = 0,1,2,3;
w0=cos/4+isin/4
=(
+i
)/2,
w1=cos3/4+isin3/4=(- +i )/2,
w2=cos5/4+isin5/4 =(- -i )/2,
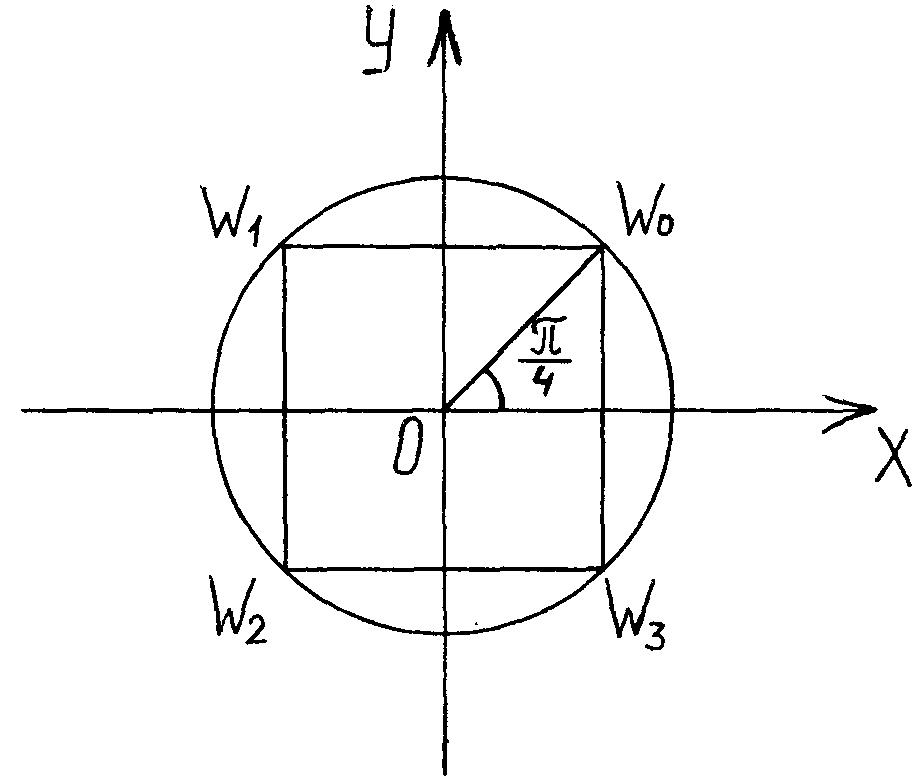
w3=cos7/4+isin7/4 =( -i )/2. Рис.1.3
На рис 1.3 построены изображения точек w0, w1, w2, w3.