
- •Введение
- •1. Элементы теории функций
- •1.1. Комплексные числа и действия над ними
- •1.1.2. Сложение и вычитание комплексных чисел
- •1.1.3. Умножение и деление комплексных чисел
- •1.2. Комплексная плоскость.
- •1.3. Комплексные функции
- •1.3.1. Комплексные функции
- •1.3.2 Комплексные функции
- •1.4. Ряды с комплексными членами
- •1.5. Элементарные функции комплексного
- •1.5.1. Показательная, тригонометрические и гиперболические функции комплексного переменного. Формулы Эйлера
- •1.5.2. Логарифмическая функция
- •1.6. Производная от функции комплексного переменного.
- •1.7. Аналитические и гармонические функции. Связь между ними
1. Элементы теории функций
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
1.1. Комплексные числа и действия над ними
1.1.1. Понятие комплексного числа.
Алгебраическая, тригонометрическая и показательная формы комплексного числа
Комплексными числами называются выражения вида
z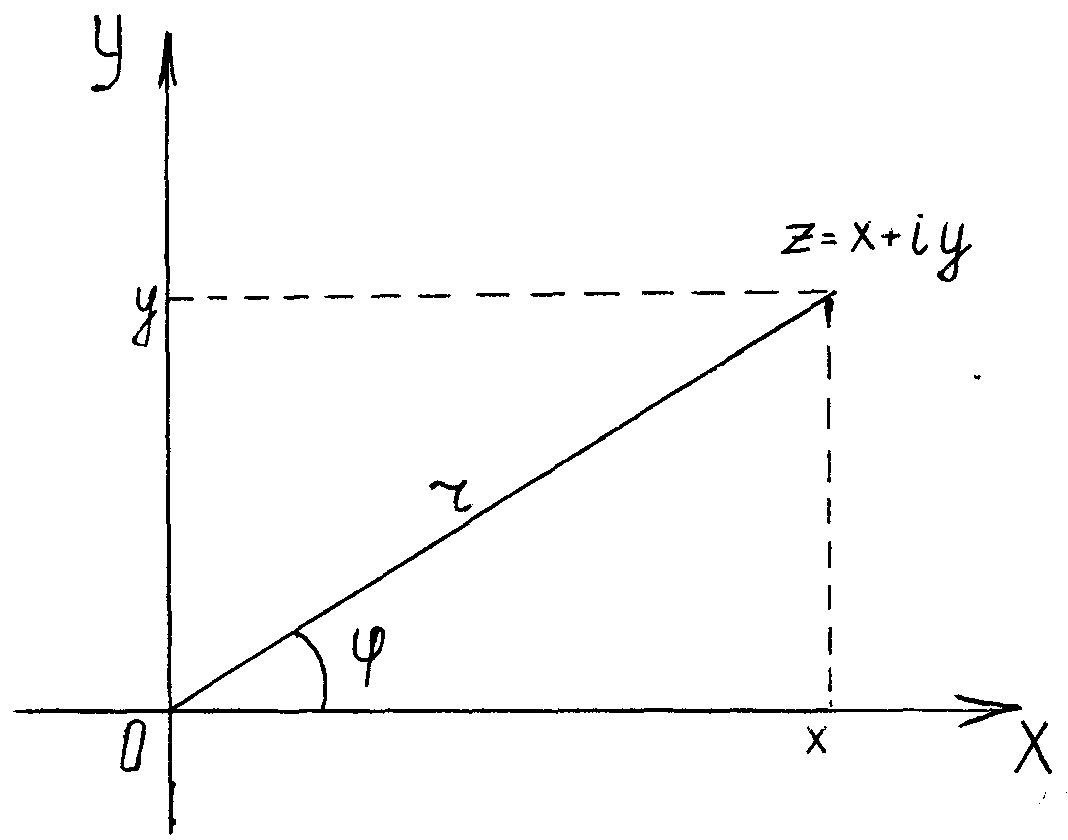 = x+iy,
где x
и y
- действительные числа, а i
- так называемая мнимая единица; так
обозначается число, квадрат которого
равен -1. Числа x
и y
называются соответственно действительной
и мнимой частью комплексного числа z
и
обозначаются x=Rez,
y=Imz.
Введем на плоскости
= x+iy,
где x
и y
- действительные числа, а i
- так называемая мнимая единица; так
обозначается число, квадрат которого
равен -1. Числа x
и y
называются соответственно действительной
и мнимой частью комплексного числа z
и
обозначаются x=Rez,
y=Imz.
Введем на плоскости
декартову систему координат
XOY (Рис. 1.1). Тогда каждому
комплексному числу z= x+iy
можно поставить в соответствие
точку (x,y) на плоскости XOY.
Таким образом, между мно-
жеством комплексных чисел Рис.1.1
и множеством точек на плоскости устанавливается взаимно однозначное соответствие: каждому комплексному числу соответствует точка на плоскости и наоборот. Плоскость, служащая для изображения комплексных чисел, называется плоскостью комплексного переменного. Действительным числам z=x соответствуют точки на оси OX, чисто мнимым числам, то есть числам вида z=iy, соответствуют точки на оси OY. Поэтому ось OX называется действительной осью, а ось OY - мнимой осью.
Два комплексных числа z1=x1+iy1 и z2=x2+iy2 считаются равными, если равны их действительные и мнимые части: z1=z2,
если x1=x2, y1=y2.
Два
комплексных числа z=x+iy
и
![]() =x-iy,
отличающиеся только знаком мнимой
части, называются комплексно сопряженными
числами. Изображения комплексно
сопряженных чисел симметричны относительно
действительной оси.
=x-iy,
отличающиеся только знаком мнимой
части, называются комплексно сопряженными
числами. Изображения комплексно
сопряженных чисел симметричны относительно
действительной оси.
Каждому комплексному числу z = x+iy можно поставить в соответствие также вектор OM, начало которого совпадает с началом координат, а конец - с точкой M(x,y). Следовательно, комплексные числа можно изображать с помощью векторов на плоскости.
Положение точки M(x,y) на плоскости можно опре-делить также с помощью полярных координат (r,). Если взять полюс в начале координат, а полярную ось направить по оси OX (рис.1.1), то x=rcos, y=rsin.
Следовательно, любое комплексное число z=x+iy можно записать в виде
z=r(cos+isin). (1.1)
Форма
записи комплексных чисел в виде (1.1)
называется тригонометрической в отличие
от алгебраической формы z=x+iy.
Число
![]() называется модулем комплексного числа
z
и обозначается z.
Число
называется аргументом комплексного
числа z
и обозначается Argz.
Аргумент определяется для любого
комплексного числа z
0 из соотношения tg=
y/x
не однозначно, а с точностью до числа,
кратного 2.
Значение аргумента, удовлетворяющее
неравенству -<,
называется главным и обозначается argz,
следовательно, Argz=argz+2n
где n
- любое целое число. Главное значение
аргумента комплексных чисел вычисляется
по формулам
называется модулем комплексного числа
z
и обозначается z.
Число
называется аргументом комплексного
числа z
и обозначается Argz.
Аргумент определяется для любого
комплексного числа z
0 из соотношения tg=
y/x
не однозначно, а с точностью до числа,
кратного 2.
Значение аргумента, удовлетворяющее
неравенству -<,
называется главным и обозначается argz,
следовательно, Argz=argz+2n
где n
- любое целое число. Главное значение
аргумента комплексных чисел вычисляется
по формулам

Если воспользоваться формулой Эйлера
cos+ isin = ei,
то любое комплексное число можно записать также в виде
z = rei (1.2)
Форма записи комплексных чисел в виде (1.2) называется показательной формой.
Два комплексных числа, заданные в тригонометрической или показательной форме, равны тогда и только тогда, когда их модули равны, а аргументы либо равны, либо отличаются на число, кратное 2.
