2. Символический метод расчета цепей с гармоническими воздействиями

Известно несколько способов представления синусоидально изменяющихся величин: в виде тригонометрических функций, в виде графиков изменения во времени, в виде вращающихся векторов и в виде комплексных чисел.

Расчет цепей периодического синусоидального тока облегчается, если изображать синусоидально изменяющиеся токи, напряжения и ЭДС векторами или комплексными числами. Установим данное соотношение.

Пусть некоторая электрическая величина (ток, напряжение, ЭДС и т.д.) изменяется по синусоидальному закону . В прямоугольной системе координат (рис. 3.12) расположим под угломвектор, длина которого в выбранном масштабе равна амплитуде(причем, > 0, если отсчитывается против часовой стрелки).

Представим себе, что вектор с момента t = 0 начинает вращаться вокруг начала координат в положительном направлении с постоянной угловой скоростью, равной угловой частоте . В момент времени t  0 вектор составляет с осью абсцисс угол . А его проекция на ось ординат будет равна мгновенному значению величиныv. Таким образом, между мгновенным значением v(t) и вектором можно установить однозначное соответствие. На этом основании будем называть векторвектором, изображающим функцию времени, и обозначать . Конечно, эти векторы, имеют смысл, отличный от смысла векторов, определяющих физические величины в пространстве (скорость, силу и др.). Поэтому такие изображения функции времени называют символическими.

Если считать ось абсцисс осью вещественных величин, а ось ординат – осью мнимых величин на комплексной плоскости, то вектор соответствует комплексному числу с модулеми аргументом. Это комплексное число называют комплексной амплитудой. Иначе говоря, это комплексная величина, не зависящая от времени, модуль и аргумент которой равны соответственно амплитуде и начальной фазе заданной синусоидальной функции.

3.3.1. Понятие о комплексных числах

Мнимая единица – это число, дающее в квадрате –1: . Введение мнимой единицы дает возможность перейти ккомплексному числу (рис. 3.13).

Применяется четыре формы записи комплексного значения синусоидальной величины:полярная, показательная, тригонометрическая и алгебраическая:

(3.29)

где и–соответственно действительная и мнимая составляющие комплексного числа; .

Переход от показательной формы к тригонометрической выполняется при помощи формулы Эйлера: . При значении углаииз формулы Эйлера следуют два часто встречающихся соотношения:и.

Операции над комплексными числами

Сопряженным комплексным числом называют число, имеющее противоположный знак фазы или мнимой части.

Если , то–комплексная амплитуда, а –комплексное изображение мгновенного значения, где называютфактором поворота, умножение на который означает поворот на угол _i в комплексной плоскости; называютфактором вращения, умножение на который означает вращение вектора с постоянной частотой  в положительном направлении вокруг начала координат.

В этой связи следует отметить, что умножение комплексного числа на «–1» означает поворот вектора на , умножение на– поворот на.

Комплексное мгновенное значение может быть представлено с помощью формулы Эйлера в тригонометрической форме . Интересующая нас функция времени, описывающая изменение тока в цепи, есть мнимая часть мгновенного комплексного значения тока:. Именно это соотношение позволяет утверждать, что между мгновенным значением синусоидальной величины и ее символическим изображением существует однозначное соответствие.

При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения, сокращенно их называют комплексными значениями, а соответствующие им векторы на комплексной плоскости – векторами комплексных значений. Связь между комплексом амплитуды и комплексом действующего значения устанавливается по формуле:

. (3.30)

Пример символического представления функции времени .

–комплекс амплитуды;

–комплекс мгновенного значения;

–комплекс действующего значения или комплекс.

Совокупность векторов комплексных значений синусоидальных величин одной частоты, изображенных на комплексной плоскости, называют векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание комплексных значений можно заменить сложением и вычитанием соответствующих векторов. Векторные диаграммы, как правило, используются для качественной оценки расчетов и их наглядности. Они являются графическим отображением математических соотношений и расчетов электрической цепи.

Взаимное расположение векторов комплексных значений на векторной диаграмме не изменится, если начальные фазы  всех комплексных значений уменьшить или увеличить на одну и ту же величину. Это означает лишь одновременный поворот всех векторов на один и тот же угол. Часто при анализе цепей векторную диаграмму строят так, чтобы вектор одного комплексного значения был направлен вдоль оси действительных величин. Такой вектор называют исходным вектором.

Направления синусоидальных величин (ток, напряжение и др.) в цепи периодически изменяются, но одно из двух направлений выбирается положительным. Это направление выбирается произвольно и показывается стрелкой на схеме соответствующего участка цепи (рис. 3.14).

При выбранном положительном направлении синусоидальная величина представляется мгновенным значением и соответствующим комплексным значением. Следовательно, взаимно однозначному представлению синусоидальных токов, напряжений и других величин в виде мгновенных и комплексных значений соответствуют их одинаковые положительные направления.

Теоремы символического метода

1. Об однозначном соответствии символического изображения данной тригонометрической функции: . Это было показано выше:, где.

2. О линейном преобразовании: если , то, т.е..

3. О сумме: если , то. Следствие:

. Следует отметить, что в правой части складываются векторы по правилам векторной алгебры.

4. О производной: если , а, тогда, т.е. взятие производной во временной области означает умножение вектора наj в комплексной области или поворот вектора на :.

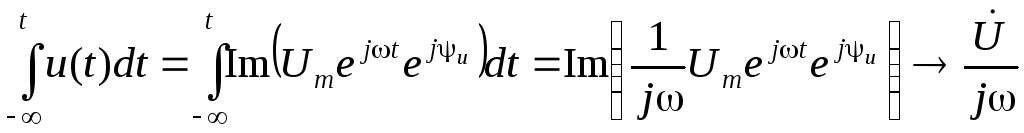5. Об интеграле: если , а, то, т.е. интегралу функции во временной области соответствует деление вектора наj в комплексной области или поворот вектора на угол .

Таким образом, символический метод позволяет свести дифференциальные уравнения, которыми описываются цепи переменного тока, к виду алгебраических уравнений. Полученное таким образом решение можно затем перевести во временную область.