Лабораторна робота № 2

МОДЕЛЮВАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ

Ціль роботи: освоєння методики моделювання лінійних диференціальних рівнянь у системі МЛЛВ і SIMULINK.

I. ТЕОРЕТИЧНІ ВІДОМОСТІ

1.1. Лінійне диференціальне рівняння.

Багато фізичних процесів, такі як коливання маятника, рух стрілки гальванометра, зміна висоти при посадці літака, процеси в електричному коливальному контурі можуть бути описані лінійним однорідним диференціальним рівнянням другого порядку

х(ї) + ах х(ґ) + а₀ х(ї) — 0. (1)

Тут а₀, аі - постійні коефіцієнти, що визначають характер процесу, крапкою позначається похідна за часом. Амплітуда змінної х(і) залежить від початкових умов, наприклад, від початкового відхилення х₀ маятника і його початкової швидкості х₀.

Вид теоретичного розв'язку диференціального рівняння (1) визначається коріннями його характеристичного полінома

р² + а₁ р + а₀ — 0.

Якщо коріння речовинне й різні р₁ = а_1-, р₂ = а₂, то розв'язок має вигляд

х(t) = Cj ea¹ + C₂ e

Якщо коріння комплексне pi,₂ =а ± ip, то розв'язок має вигляд

x(t) = C₁ eat sin fit + C₂ eat cos fit.

Постійні З₁ і З₂ знаходять, підставляючи початкові умови у вираження для x(t) і x (t) при t = 0.

Приклад 1. Дане диференціальне рівняння

x + 2 x + 2x = 0, x₀ = x₀ = 1.

Його характеристичне рівняння p + 2p + 2 = 0 має коріння p₁₂ =-1 ± i. Отже, загальний розв'язок буде наступним: x(t) = C₁e- sint + C₂е cost.

Диференціюючи, знаходимо вираження для x:

x(t) = -(C₁ + C₂ )e-t sin t + (C₁ - C₂ )e-t cos t. При t = 0 з урахуванням початкових умов одержуємо C₁ = 2, З₂ = 1. Отже,

x(t) = е ^-1 (2sin t + cost).

Ефективним засобом розв'язку диференціальних рівнянь є чисельне моделювання в одному з математичних пакетів (MATHCAD, MATLAB, SIMULINK і ін.). Графік розв'язку x(t) спостерігається на екрані дисплея. У пакеті MATLAB для цієї мети є команди initial, lsim, ode23, ode45, dsolve. Додаткові можливості для користувача надає моделювання в SIMULINK.

1.2. Структурне моделювання лінійних диференціальних рівнянь.

При структурному моделюванні диференціальних рівнянь у пакеті SIMULINK необхідно скласти схему моделювання. На ній зображуються обчислювальні блоки (підсилювачі, суматори, інтегратори) і зв'язку між ними. При проведенні моделювання ця схема набирається на екрані дисплея за допомогою миші або клавіатури. По своєму змісту цей процес аналогічний уведенню програми, однак він більш простий і наочний. Докладна інформація про реалізацію таких схем в SIMULINK є в розділі 3 навчального посібника Мироновского Л.А., Петровой К.Ю. «Введення вМАПЛБ» (ГУАП, 2006).

Розглянемо методику складання схеми моделювання на прикладі однорідного лінійного диференціального рівняння другого порядку

X + 2Х + 3х = 0, х(0) = 2, Х(0) = 4. (2)

Для побудови схеми моделювання скористаємося методом зниження похідній (методом Кельвіна). У ньому можна виділити чотири кроки.

Крок 1 Дозволяємо вихідне рівняння щодо старшої похідної. Зокрема для рівняння (2) одержуємо X = -2X - 3х.

Крок 2. Уважаємося старшу похідну відомої й виконуємо її послідовне інтегрування, одержуючи всі нижчі похідні й саму змінну х. У випадку рівняння (2) для цього буде потрібно два послідовно включені інтегратори, на виходах яких одержимо сигнали X і х.

Крок 3. Формуємо старшу похідну, використовуючи рівняння, отримане на першому кроці. У нашому прикладі для цього буде потрібно суматор, що складає сигнали X і х, домноженные, відповідно, на коефіцієнти -2 і -3.

Крок 4. Поєднуємо схеми, отримані на другому й третьому кроках, у загальну схему моделювання, указуємо початкові умови інтеграторів.

Вихідний сигнал схеми подається на імітатор осцилографа (блок Scope) або передається в робочий простір MATLAB (блоки OUT або Toworkspase).

Застосування цієї методики для рівняння (2) приводить до схеми, показаної на мал. 1. Вона містить два інтегратори, два масштабні підсилювачі й суматор (позначений кружечком).

1.3. Системи лінійних диференціальних рівнянь першого порядку.

Багато технічних об'єктів можна описати системою п лінійних диференціальних рівнянь першого порядку:

— = АУ + Ьи, (3)

Ж

де й - вхідний сигнал; Y - вектор-стовпець вихідних змінних в-у-; Ь - вектор-стовпець коефіцієнтів Ь{; А - квадратна матриця коефіцієнтів а, ] = 1, п.

Наприклад, при моделюванні літального апарата складовими вектора Y можуть бути поточні координати літака й швидкості їх зміни, тоді матриця А буде характеризувати динаміку літака, а доданок Ьи описувати керуючі впливи, формовані льотчиком або автопілотом.

Один з методів розв'язку системи диференціальних рівнянь заснований на попередньому переході від системи (3) до одному рівнянню п-го порядку. Для цього з рівнянь системи й з рівнянь, отриманих їхнім диференціюванням, виключають усі змінні крім однієї. Для неї одержують одне диференціальне рівняння. Вирішуючи його, визначають цю змінну, а інші знаходять, по можливості, без інтегрування. Приклад 2. Дана система із двох диференціальних рівнянь

^в1 = ³В " ²В2 + ⁵ (₄₎

^в2 ="⁶В1 " В2.

Після диференціювання першого рівняння одержуємо:

В = 3в - 2В2 = 21в - 4в2 +15.

Щоб виключити в₂, віднімемо звідси подвоєне перше рівняння системи (4):

^в1 ^{- 2}В ^{- 15}В1 = ⁵.

Ми одержали лінійне неоднорідне диференціальне рівняння другого порядку. Загальний розв'язок цього рівняння являє собою суму загального розв'язку відповідного однорідного рівняння й приватного розв'язку в₁ = у°^дн + в\^аст'. Тому що коріння характеристичного рівняння р - 2р-15 = 0 речовинні й різні: р\ = -3, р₂ = 5, то розв'язок у°^дн' має вигляд З₁е+ З₂е⁵'. Складаючи його із приватним розв'язком в1^аст = = -1,

одержуємо в₁ = З₁е + З₂е⁵ -1/3. Змінну в₂ знаходимо зі співвідношення

в₂ = 0,5(3в + 5 - В1) = 3С1е³ - З₂е⁵ + 2.

Для визначення постійних коефіцієнтів З1 і З₂ використовують початкові умови системи. Аналогічним образом цей метод застосовується й для систем рівнянь більш високих порядків

1.4. Моделювання системи лінійних диференціальних рівнянь.

Якщо завдання описується системою диференціальних рівнянь першого порядку, то для її моделювання по методу зниження похідній досить скласти схеми для кожного рівняння окремо. Наприклад, схема моделювання системи рівнянь (4) буде мати вигляд, показаний на мал. 2.

5

Рис. 2. Схема моделювання системи рівнянь (4)

Для спостереження графіків сигналів yi(0, y₂(t) в SIMULINK використовується блок осцилографа SCOPE, а для спостереження фазової траєкторії в₂ = f (в₁) - блок осцилографа XY Graph.

2. ЗАВДАННЯ ПО РОБОТІ Й ЗМІСТ ЗВІТУ

• Теоретичний розв'язок рівняння (1) при заданих значеннях а₀, а₁ і початкових умовах x(0) = 5, x(0) = 0 . Таблиці розрахункових даних, графіки розв'язків x(t), x(t), графік фазового портрета X = f(x).

• Схема моделювання заданого рівняння стосовно до SIMULINK.

Теоретичний розв'язок системи диференціальних рівнянь (3) для випадку

A =	a11 a12	, b =	T	, Y =	' В1"
	0 a22 _		0		_ В2 _

0 20

(5)

Y (0) =

x = 5,

при заданих значеннях агов. Графіки розв'язків в) і в₂(0 і графік фазового портрета В2 = /⁽В1⁾.

Схема моделювання вихідної системи рівнянь стосовно до SIMULINK. 3. ПОРЯДОК ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ

• Набрати в SIMULINK схему моделювання рівняння (1), установити коефіцієнти й початкові умови.

• Одержати осциллограммы х(), х) і х) = /(х), зрівняти їх з теоретичними графіками. Варіювати крок і метод інтегрування.

• Набрати схему моделювання системи рівнянь (3), установити коефіцієнти й початкові умови (5).

• Одержати осциллограммы в₁(), в₂(0 і в₂ = /(в₁), зрівняти їх з теоретичними графіками. Варіювати крок і метод інтегрування.

• Виконати моделювання системи рівнянь (3) у МАТЬАБ, використовуючи команду Ыт. Зрівняти графіки, отримані в МАТЬАБ і SIMULINK.

4. КОНТРОЛЬНІ ПИТАННЯ

• Розв'язати наступні лінійні диференціальні рівняння:

а) x - 2x + x = 4, x(0) = 1, x(0) = 2, x (0) = -2.

б) x + 4x = sin2t, x(0) = x(0) = 0.

• При якому значенні а й при яких початкових умовах розв'язок рівняння x + ax + x = 0 має вигляд:

a) x = sin t; б) x = cos t; в) x = el ; г) x = e-t ; d) x = e³ ; е) x = et ^/3 .

• У чому полягає метод зниження похідній? Користуючись цим методом, скласти схеми моделювання для всіх варіантів п. 1.

• Використовуючи метод зниження похідній, скласти схеми моделювання наступних диференціальних рівнянь:

a) x -1 = 0, x(0) = x(0) = 1,5; б) x = x, x(0) = x(0) = -1;

в) x + 2x + 7x = -8, x(0) = -10, x(0) = -5, x(0) = 3;

г) x^(6; = 0, x(0) = x(0) = x(0) = x (0) = 0, x^(4; (0) = -2.

• Схема моделювання являє собою кільце із трьох інтеграторів з одиничними коефіцієнтами й однаковими початковими умовами. Знайти моделируемое диференціальне рівняння і його аналітичний розв'язок.

• Як зміняться графіки розв'язку лінійного однорідного диференціального рівняння при заміні знаків усіх початкових умов на протилежні?

• Описати процедуру переходу від системи диференціальних рівнянь до одному рівнянню й зворотну процедуру, розглянувши випадок n=3. Привести приклад.

• Скласти схему моделювання й знайти розв'язок системи лінійних диференціальних рівнянь Y = AY, y_{ (0) = 1, якщо матриця A має вигляд

	"0	1	1"
a) A =	1	0	1	, б) A =
	1	1	0

0 1 1 -1 0 1

-1 -1 0

11 11

в) A =

ВАРІАНТИ ЗАВДАННІ ПО РОБОТІ № 2

1

2

3

4

5

6

7

8

9

10

11

12

№

0,1 0,4 -1,0

1,0 -2,0

0,1 1,6 -1,0

0,8 -1,8

0,5 4,8 -1,0

0,7 -1,7

0,1 0,5 -1,0

0,6 -1,6

0,1 1,8 -1,0

0,57 -1,5

0,5 5,0 -1,0

0,4 -1,4

0,1 0,6 -1,0

0.35 -1,3

0,1 2,0 -0,9

1,0 -1,9

0,5 5,4 -0,9

0,8 -1,7

0,1 0,7 -0,9

0,7 -1,6

0,1 2,2 -0,9

0,6 -1,5

0,6 5,8 -0,9

0,5 -1,4

Ai

ao aii

ai2

A22

13

14

15

16

17

18

19

20

21

22

23

24

№

0,1 0,8 -0,9

0,4

-1,3

0,3 2,4 -0,9

0,3

-1,6

0

6,0

-0,8

1,0

-1,6

0,9 8,8 -0,8

0,8

-1,6

0,1 0,9 -0,8

0,7

-1,5

0,3 2,6 -0,8

0,6

-1,4

0,7 6,4 -0,8

0.5

-1,3

1.1

9,0 -0,8

0,4

-1,2

0,2 1,0 -0,8

0,3

-1,1

0,3 2,8 -0,5

1,0

-1,5

0,8 6,8 -0,5

0,8

-1,3

0,6 5,8 -0,5

0,7

-1,2

^a1 a0

^a11 ^a12 ^a22

Лабораторна робота №3

МОДЕЛЮВАННЯ СИСТЕМИ, ЩО СТЕЖИТЬ

Ціль роботи: освоїти різні способи опису лінійних динамічних систем і методи їх моделювання в пакетах МААВ і SIMULINK.

1. Теоретичні відомості

1.1. Опис систем структурною схемою й передатною функцією.

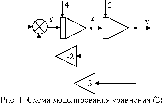
В інженерній практиці використовуються різні способи завдання динамічних систем - за допомогою структурних схем, передатних функцій, диференціальних рівнянь, а також за допомогою частотних і тимчасових характеристик. Проілюструємо їх на прикладі системи, що стежить, структурна схема якої представлена на мал.1. До її складу входять інерційна підсилювальна ланка з передатною функцією до / (Т₁ р + 1), двигун з передатною функцією 1 / (Т₂ р), що й віднімає пристрій для порівняння вхідного сигналу і й вихідного сигналу системи, що стежить, в. система, що стежить, повинна працювати таким чином, щоб кут повороту двигуна в по можливості точно рівнявся значенню вхідного сигналу й (завдання спостереження).

k	X1 ь	1
T p +1	f	T2 p

Х2

y

u

e

Рис. 1. Структура системи, що стежить

Спосіб завдання моделей об'єктів за допомогою схеми (типу наведеної на мал.1) називається структурним, оскільки він відбиває реальну структуру об'єкта.

По передатних функціях окремих блоків можна побудувати загальну передатну

В ( р)

функцію системи, що стежить, Q(p) =, що зв'язує зображення за Лапласом входно-

^{і (} Р)

го й вихідного сигналів.

Для цього у відповідності зі структурною схемою виписується система рівнянь

1 k Y ( Р) = e( Р),

T₂p (Txp +1)

яка потім перетвориться до одному рівнянню, шляхом виключення змінної e(p):

Y (Р) =

к

(U(p) - Y(p)).

T₂ p • (Tip + 1)

e(p) = U(p) - Y(p),

(1)

Далі, виражаючи вихідний сигнал Y(p) через вхідний U(p), одержуємо

Y (p) =

к

і(p) = Q(p) • U(p).

T p • (T p +1) + k

де Q(p) - передатна функція системи.

У нашому випадку вона має вигляд

до

^Q(p)= Titp² + T₂p+ до ' У порівнянні зі структурним описом передатна функція є більш компактною математичною моделлю, у той же час вона дозволяє аналізувати такі характеристики, як стійкість і мінімальність об'єкта.

1.2. Опис систем диференціальними рівняннями.

Від передатної функції легко здійснити перехід до опису системи за допомогою диференціального рівняння. У розглянутому випадку для цього досить у рівнянні

(TT p² + T2 p + к)Y (p) = ku ( p) розкрити дужки й замінити оператор p оператором диференціювання d/dt

TIT2 y + T2 y + ky = ku. (2)

Вирішуючи це диференціальне рівняння, можна знайти реакцію системи, що стежить, на будь-який вхідний вплив.

Аналітичний розв'язок y(t) диференціального рівняння (2) є сумою розв'язку однорідного рівняння у_одн(0 і частки розв'язку диференціального рівняння

Участн⁽0.

Для одержання у_одн (t) становимо характеристичне рівняння T₁T₂p² + T₂p + до = 0. і знаходимо його коріння p₁ і p₂. Якщо вони речовинні й різні, то розв'язок однорідного

рівняння шукається у вигляді у_од_н (t) = C1ep^1t + C2 ep^2t, де З₁ і З₂ - коефіцієнти, що залежать від початкових умов і обумовлені надалі. Якщо коріння однакове (кратні) p₁=p₂, то розв'язок має вигляд у_одн (t) = (C₁ + C₂₁)ep^1t. Парі комплексного корінь p₁,₂= а ± jp відповідає розв'язок у_одн (t) = eat (C₁ sin fit + C₂ cos fi t).

У всіх випадках система виявляється стійкої, якщо коріння лежало в лівій півплощині ( при цьому розв'язок однорідного рівняння із часом прагне до нуля).

Приватний розв'язок диференціального рівняння визначається видом правої частини диференціального рівняння (2). Якщо, наприклад, там коштує експонентна функція u=e-, то й приватний розв'язок потрібно шукати у вигляді експоненти у_част_н =Ce^-. Якщо u = 1(t), його слід шукати у вигляді константи у_частн = C. Для визначення C треба підставити приватний розв'язок у диференціальне рівняння. Враховуючи, що похідна від константи дорівнює нулю, знаходимо, що в останньому випадку C = 1.

Значення постійних З₁, З₂ визначаються шляхом підстановки в отриманий розв'язок початкових умов. Наприклад, у випадку нульових початкових умов і розв'язку виду y(t) = C₁ ept + C₂ eplt +1 постійні З₁ і З₂ перебувають із системи рівнянь

З + З2 + 1 = 0; Р1С1 + Р2С2 = 0.

Поряд із завданням об'єкта одним диференціальним рівнянням типу (2) часто використовують опис за допомогою системи диференціальних рівнянь першого порядку. Воно відомо як матричний опис або опис у просторі станів.

Для одержання опису системи, що стежить, у просторі станів виберемо як змінних стану х₁ і х₂ вихідні сигнали ланок першого порядку на структурній схемі мал. 1.

Складемо для кожного з них диференціальне рівняння першого порядку

1 k k 1

^Х1 = T ^Х1 T ^Х2 T ^T1 ^T1 ^T1

^X2 rp ^X1. •

^T2

Крім того, запишемо алгебраїчне рівняння для вихідного сигналу в = х₂ . У матричному виді цей опис має вигляд

X = AX + bu, y = cx,

де

				"-1/T	- k / t "
X =	1		, A =	1/T2
	_ Х 2 _				0
		"k / t "
, b =
		0

[0 1].

c =

Аналізуючи цей опис, можна оцінити стійкість, керованість, наблюдаемость і інші характеристики системи.

1.3. Взаємозв'язок описів.

Усі розглянуті види описів тісно взаємозалежні, тому, знаючи одне з них, можна одержати інші. Наприклад, зв'язок між матрицями A, b, c опису в просторі станів і передатною функцією системи Q(p) задається рівнянням

Q( p) = c( pe - A)"¹b, (3)

де p - оператор Лапласа, E - одинична матриця.

Кожне з розглянутих описів системи дозволяє розраховувати її реакцію на типові вхідні сигнали. Найчастіше систему характеризують реакцією на дельта-функцію й = S(t) і на одиничну функцію (функцію одиничного стрибка) і = 1(t). Ці реакції відомі як імпульсна вагова характеристика системи y = q(t) і перехідна характеристика В = P(t). Їхні зображення за Лапласом пов'язані з передатною функцією формулами

q(t) про Q(p); p(t) про Q(p)/p, (4)

які зручно використовувати для знаходження вагарні й перехідної характеристики.

Інший підхід до опису системи пов'язаний з використанням частотних характеристик. Вони виходять розглядом функції комплексної змінної, одержуваної з формули (3) заміною p = у'ш: Q(jra) = з(/шЕ - A) ^{- 1} b.

1.4. Моделювання в пакеті MATLAB і SIMULINK

Пакет MATLAB підтримує всі види описів динамічних систем, включаючи структурні схеми, передатні функції й матричний опис у просторі станів. Для роботи зі структурними схемами в пакеті MATLAB є додаток SIMULINK. Його можна викликати, набираючи в командному вікні MATLAB команду simulink.

Чисельне моделювання системи, що стежить, в MATLAB виконується за допомогою команд impulse, step, lsim. Попередньо треба ввести чисельник num і знаменник den передатної функції або матриці A, B, C, D опису в просторі станів і сформувати структуру sys=tf(num,den) або sys=ss(A,B,C,D). Після цього вагова функція й перехідна функція перебувають командами impulse(sys), step(sys), а реакції на довільні вхідні сигнали, такі як і= е-е^-, розраховуються за допомогою команди lsim.

Реалізація різних з'єднань блоків може бути здійснена програмно за допомогою команд parallel, series, feedback, append і деяких інших. Для цієї мети можна використовувати також команди +, -, *.

В MATLAB можна одержувати не тільки чисельне, але й символьний розв'язок диференціальних рівнянь. Це робиться за допомогою команди dsolve тулбокса SYMBOLIC. Вхідними аргументами команди служать диференціальне рівняння й початкові умови. Наприклад, для розв'язку диференціального рівняння y + 2 y + 3 y = 2 з нульовими початковими умовами слід набрати код >> y=dsolve('D2y+3*Dy+2*y=2', 'Dy(0)=0','y(0)=0') MATLAB видасть відповідь y =1+exp(-2*t)-2*exp(-t), тобто y=1+e~^2t-2e-t.

2. ЗАВДАННЯ ПО РОБОТІ Й ЗМІСТ ЗВІТУ

У роботі досліджується динаміка системи, що стежить, заданою структурною схемою (мал.1) при значеннях параметрів до, T₁, T₂, наведених у таблиці варіантів завдань. Звіт по роботі повинен містити:

• Вихідну схему моделювання із заданими чисельними значеннями параметрів і передатну функцію Q(p), отриману з рівняння (1).

• Диференціальне рівняння другого порядку, що описує систему, що стежить, його аналітичний розв'язок і графік вихідного сигналу y(t) при вхідному сигналі u=e- і нульових початкових умовах.

• Опис системи, що стежить, у просторі станів, передатну функцію системи, отриману по формулі (3). Формули й графіки вагарні й перехідний характеристик.

• Схеми моделювання, що стежить системи стосовно до SIMULINK генератори, що містять осцилографи й, вхідних сигналів ( для генерування сигналу u=e- використовувати інтегратор зі зворотним зв'язком). Програми чисельного й символьного моделювання в MATLAB.

3. ПОРЯДОК ВИКОНАННЯ РОБОТИ

• За допомогою пакета SIMULINK побудувати схему моделювання відповідно до мал. 1.

Одержати графіки вихідних сигналів (вагарні функції, перехідної функції й реакції на u=e-). Перевірити їхня відповідність розрахунковою.

• Паралельно зі схемою моделювання системи, що стежить, набрати модель передатної функції Q(p) системи, що стежить, і зрівняти їхні вихідні сигнали.

• Виконати моделювання в пакеті MATLAB, використовуючи різні описи системи. Зрівняти результати моделювання в MATLAB і SIMULINK.

• Побудувати графіки фазових траєкторій у площині (х₁, x₂) (в SIMULINK для цього буде потрібно блок Xy-graph). Побудувати частотні характеристики системи, що стежить, використовуючи команди bode, nyquist, ltiview.

4. КОНТРОЛЬНІ ПИТАННЯ

• Описати загальну процедуру переходу від довільної структурної схеми до системи лінійних диференціальних рівнянь першого порядку.

• Знайти реакцію свого варіанта системи, що стежить, на вхідний сигнал u = t і побудувати графік вихідного сигналу.

• Знайти передатну функцію системи, що стежить, якщо пристрій порівняння реалізований відповідно до однієї з наступних формул:

е = і - в, е = і - ку, е + е = і + і - в.

• Як вплине зміна знака зворотному зв'язка в системі, що стежить, на її стійкість і вид перехідної характеристики?

• Знайти передатну функцію системи, що стежить, якщо передатна функція двигуна рівна

1 1 р ^а) Т_хр +1' ^б) Т_хр - 1^{, в)} Т₂р +1 •

• Знайти матриці опису в просторі стану для пп. 3 і 5.

• Зрівняти графіки вагарні й перехідний функцій розімкнутої й замкненої системи для свого варіанта завдань.

5. ВАРІАНТИ ЗАВДАНЬ

№	1	2	3	4	5	6	7	8	9	10
k	4	16	21	7	3	15	12	5	10	16
тх	0,2	0,1	0,1	0,125	0,25	0,125	0,2	0,4	0,8	1,2
Т2	5	20	5	4	8	4	8	2	2.5	5

№	11	12	13	14	15	16	17	18	19	20
k	6	8	10	12	14	16	20	18	16	12
Т1	0,75	1,25	1,5	2	2,5	2	1,5	0,8	0,4	0,8
Т2	4	4	2	3	2	5	10	5	8	5