3. Математический анализ и обработка навигационной информации

3. Рис 3

3. Б

1. Случайные величины

Случайная величина ─ это величина, которая может принимать то или иное значение неизвестное до опыта. Под случайной величиной понимают всю совокупность значений, которые она может принимать.

Если случайная величина Х измерена п раз, то значения (результаты измерений) называются ее реализациями в данной серии.

Случайная величина называется дискретной, если все ее значения можно перечислить. Например, количество очков на гранях игрального кубика, погрешности в 0,1^о при округлении поправки компаса.

Если случайная величина своими значениями заполняет некоторый числовой интервал, то она называется непрерывной. Например, площадь пробоины, время до первого отказа прибора.

Поскольку случайная величина может принимать различные значения, важно знать, с какой вероятностью могут появляться те или иные ее значения. Зависимость между самой случайной величиной и вероятностью появления ее возможных значений называется законом распределения случайной величины.

Закон распределения может быть представлен в трех видах: ряд распределения, функция распределения и плотность распределения.

Самый простой вид − ряд распределения. Он представляет собой таблицу, где каждому значению случайной величины соответствует вероятность ее появления:

х1	х2	х3	…	хп
Р1	Р2	Р3	…	Рп

Естественно, что перечислить все x_i можно только для дискретных случайных величин и ряд распределения возможен только для них.

Второй вид − функция распределения F(x). Она показывает, чему равна вероятность того, что случайная величина не превосходит данное значение х, т.е. F(x) = Р( Х ≤ х ).

Для того, чтобы найти F(x) надо суммировать вероятности всех значений Х ≤ х. Для дискретных величин это можно сделать простым суммированием, а для непрерывных − интегрированием от - ∞ до х. Поэтому F(x) называют еще интегральной функцией распределения.

1. Функции распределения случайных величин: а) дискретная; б) непрерывная

Увеличивая Х, можно накрыть интервал всех возможных значений случайной величины, т.е. F(x) стремится к 1.

Третий вид, в котором может быть представлен закон распределения случайной величины, − плотность распределения f (x).

Рассмотрим рис. 3.1 б. Очевидно, что чем круче идет кривая F(x), тем бóльшие вероятности суммируются, т.е. для участков с более вероятными значениями кривая имеет больший наклон к оси Х. Тангенс угла наклона кривой есть производная от этой функции. Производная от функции распределения называется плотностью распределения: F' (x) = f (x).

Производную имеют только непрерывные функции, поэтому плотность распределения существует только для непрерывных случайных величин. На рис. 3.2 показана плотность распределения одной из случайных величин.

На графике плотности распределения хорошо видно, где наиболее вероятные значения случайной величины (около максимума f (x) ), а где менее вероятные.

Вероятность того, что случайная величина заключена в пределах от  до β, равна площади под кривой в этом интервале и может быть найдена путем интегрирования:

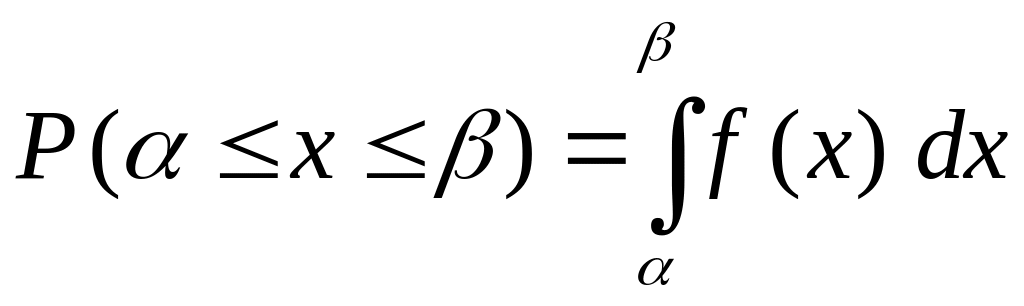
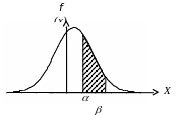
2. Плотность распределения случайной величины.

Так как в интервале от - ∞ до + ∞ случайная величина какое-то значение принимает с неизбежностью, площадь под всей кривой f (x) равна 1. Плотность вероятности полностью характеризует случайную величину.