4. Решение сферических треугольников

Решить треугольник означает по трем заданным элементам найти остальные три. Порядок решения с помощью калькулятора следующий.

Начертить треугольник и обозначить заданные элементы.

1. Подобрать теоремы и привести формулы к рабочему виду. Это означает перенести все известные в одну сторону уравнения и оставить функции только sin, cos, tg, т.е. только те функции, которые есть на клавиатуре калькулятора.

2. Произвести набор на клавиатуре калькулятора в соответствии с рабочей формулой.

3. Проанализировать ответ и записать его. Если ответ получился отрицательным, добавить к нему 180^о. Если вычисления производились по теореме синусов, определить четверть, в которой лежит найденный элемент, по величине противолежащего элемента (против угла больше 90^о лежит сторона больше 90^о и наоборот).

При подборе теорем рекомендуется пользоваться только тремя заданными элементами (так называемое, независимое решение) и не брать вновь найденные элементы.

Если при решении необходимо записывать промежуточные результаты, надо сохранять пять знаков после запятой.

Решение сферических треугольников в задачах судовождения

Покажем, как применяются теоремы сферической тригонометрии для решения конкретных судоводительских задач.

Судно совершает плавание по дуге большого круга из точки А в точку В. На рис. 2.5 показаны меридианы этих точек и экватор.

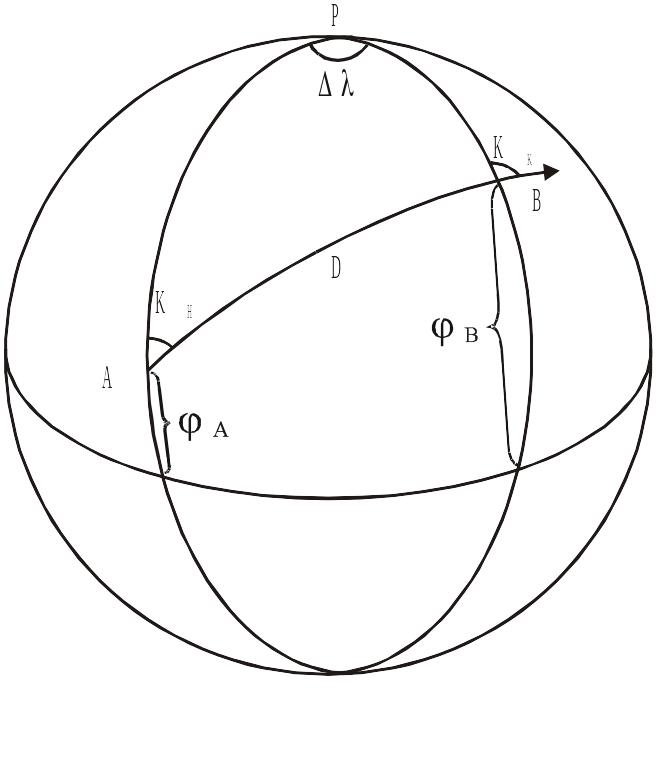
5. Плавание по дуге большого круга

Точкой Р обозначен полюс. Координаты точек А и В заданы. Это означает, что известны стороны РА и РВ (дополнение соответствующих широт до 90^о) и сферический угол при полюсе (разность долгот). Требуется найти плавание D, курс начальный К_н и конечный – К_к.

Как видно на рис. 2.5, в сферическом треугольнике РАВ даны две стороны и угол между ними. Воспользуемся теоремами косинуса стороны и четырех рядом лежащих элементов.

cos D = cos (90^o -__A) cos (90^o -_B) + sin (90^o - _A) sin (90^o -_B) cos ;

ctg A sin = ctg (90^o -_B) sin (90^o -_A) - cos (90^o -_A) cos ;

;

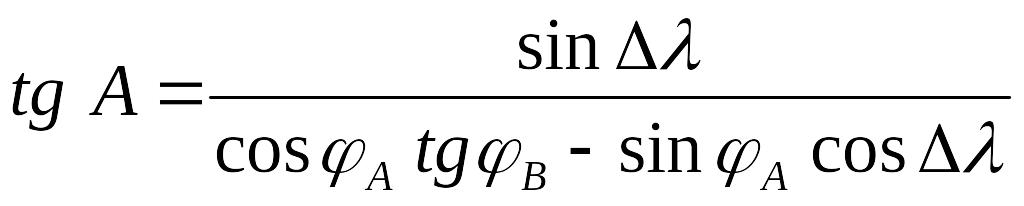ctg B sin = ctg (90^o -_A) sin (90^o -_B) - cos (90^o -_B) cos ;

.

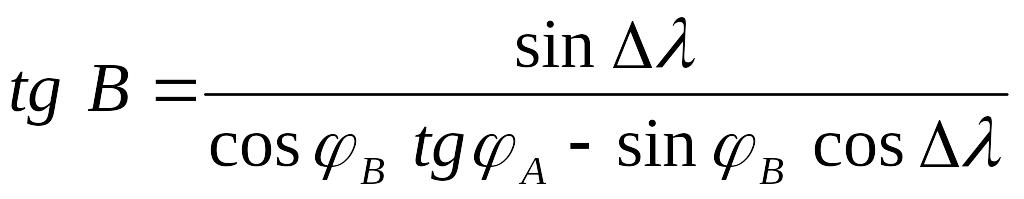Подставляя заданные координаты в рабочие формулы , и , находим D, А и В. На рис. 4 видно, что угол А равен начальному курсу, а конечный курс равен 180^о- В. Найденное значение D в градусах умножаем на 60, чтобы получить минуты, т.е. морские мили.

Следует иметь в виду, что в формулах − значение определяет величину сферического угла при полюсе безотносительно к полушарию восточному или западному, т.е. подставляется туда по модулю.

6. Параллактический треугольник

На рис. 2.6 схематично изображаем треугольник на небесной сфере, который называется параллактическим. Его решение заключается в нахождении высоты и азимута светила. Исходными данными являются: ,  и t.

Высоту светила находим по теореме косинуса стороны:

Для нахождения азимута воспользуемся теоремой котангенсов:

Следует заметить, что, так как в сферическом треугольнике ни один элемент не может быть больше 180^о, азимут получается в полукруговом счете и его перевод в истинный пеленг требует дополнительного анализа.