2. Взаимополярные треугольники

Пусть задан сферический треугольник ABC (рис. 2.3). Из вер­шины А как из полюса построим сферическим радиусом AM = 90° дугу а' большого круга. Точно так же из полюсов В и С сфериче­скими радиусами ВК и CL построим дуги b' и с' больших кругов. Эти три дуги, пересекаясь образуют новый сферический треуголь­ник с вершинами А', В' и С'. (Поскольку на рис. 2.3 у исходного треугольника ABC каждая из сторон предполагается меньше 90°, то он расположен внутри треугольника А'В'С'. В других случаях стороны треугольников будут пересекаться.) Далее из того же рисунка следует, что дуги C'N, В'М и A'L есть сферические ра­диусы сторон заданного тре­угольника ABC с полюсами в вершинах А', В' и С'.

Таким образом, имеем два сферических треугольника, у ко­торых вершины одного являют­ся полюсами сторон другого. Такие треугольники называют­ся взаимополярными.

Рассмотрим зависимость ме­жду элементами взаимополярных треугольников. С этой целью найдем сумму угла А внутреннего треугольника и стороны а' внешнего. Из рис. 2.3: , следовательно .

Но сумма дуг — это сферический радиус стороны с внутреннего треугольника с полюсом в вершине С, а сумма дуг - сферический радиус стороны и с полюсом в вершине В'. Каждый радиус равен 90°. Поэтому

А + а' = 180°; В + b' = 180°; С + с' = 180°.

Полученные равенства выражают первое свойство элементов взаимополярных треугольников.

Для вывода второго свойства найдем сумму угла А' внешнего и стороны а внутреннего треугольников. Угол А' измеряется ду­гой большого круга KL: А' = . Поэтому А' + а = , но = 90° и = 90° как сферические радиусы сторон b' и с' соответствен­но. Следовательно,

.

Свойства взаимополярных треугольников используются при вы­воде некоторых формул и при решении практических задач сфериче­ской тригонометрии.

3. Теоремы сферической тригонометрии

Задачей сферической тригонометрии является установление за­висимостей между сторонами и углами сферического треугольни­ка. Сферический треугольник считается заданным, если известны какие-либо три его элемента. Под решением треугольника подразу­мевается отыскание его неизвестных элементов. В большинстве случаев решение выполняется по так называемым основным форму­лам, к которым относятся: формула косинуса стороны; формула ко­синуса угла; формула синусов; формула котангенсов, называемая также формулой четырех рядом лежащих элементов.

Зависимости между элементами сферического треугольника, выражаемые первыми тремя формулами, называют теоремами.

Каждая формула связывает три известных (заданных) элемента с одним из неизвестных. Наряду с выводами основных формул ни­же приводится вывод однотипной с ними формулы пяти элементов.

Формула косинуса стороны (теорема косинусов). Построим сфе­рический треугольник ABC и трехгранник с вершиной в точке О (рис. 2.4). В вершине А проведем касательные к сторонам b и с тре­угольника. Касательные пересекутся в точках N и М с продолжен­ными ребрами трехгранника. Заметим, что все три ребра трехгран­ника равны радиусу R сферы.

Дважды используя теорему квадрата стороны плоского косо­угольного треугольника, найдем сторону NМ сначала из треуголь­ника NAM, а затем из треугольника NOM:

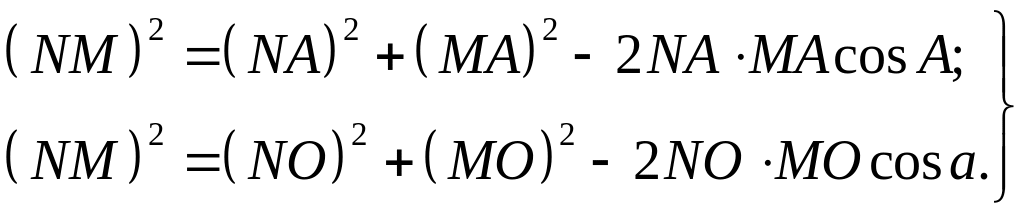
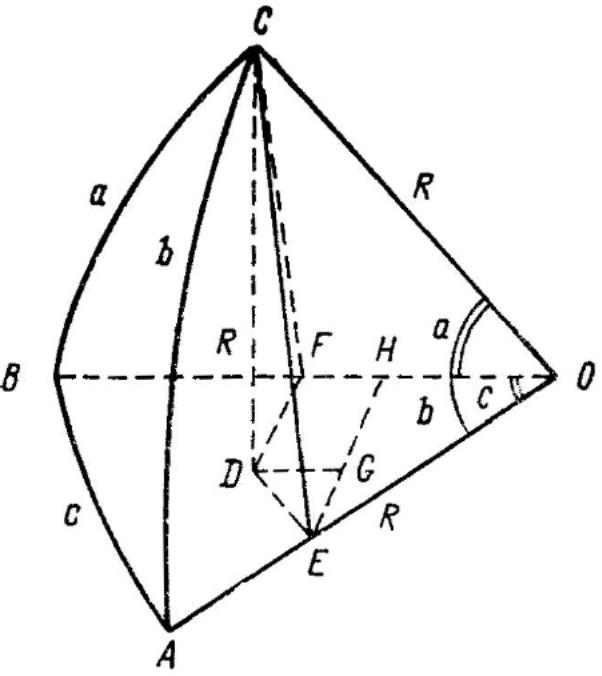
4. Графические построения к выводу формул сферического треугольника

Теперь в плоских прямоугольных треугольниках NAO и МАО найдем гипотенузы NO и МО:

.

Подставим величину квадратов гипотенуз в выражения и приравняем правые части этих выражений: (NA)² + (MA)² – 2NAMA cos A = (NA)² + (MA)² + R² – 2NOMO cos a. Пос­ле приведения подобных членов и сокращения на 2 перегруппируем слагаемые и поделим их почленно на NO и МО: . Так как в плоских прямоугольных треугольниках NAO и MAO: , то окончательно получим .

Выведенная формула справедлива одновременно и для углов трехгранника, и для элементов сферического треугольника, мерой которых служат углы трехгранника.

Формула косинуса стороны читается так: в сферическом тре­угольнике косинус стороны равен произведению косинусов двух дру­гих сторон плюс произведение синусов этих сторон на косинус угла между ними (... на косинус угла, противолежащего исходной сто­роне).

Формула косинуса стороны связывает стороны и один из углов сферического треугольника. Всего таких формул три:

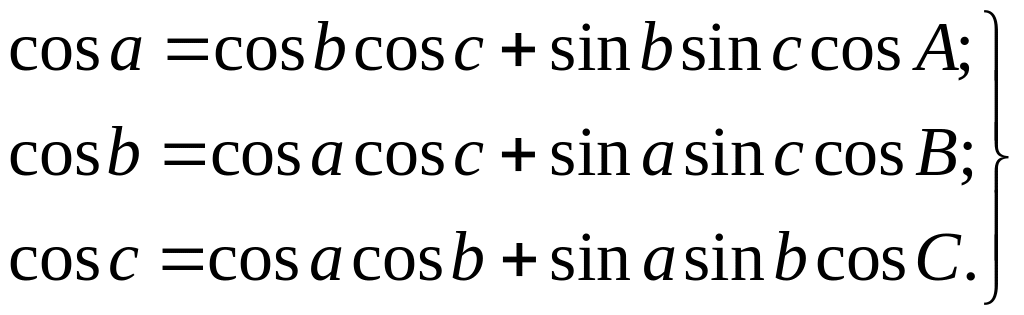
Формула косинуса угла (теорема косинусов для полярного тре­угольника). Эта формула выражает зависимость между тремя угла­ми и стороной сферического треугольника. Ее можно вывести, ис­пользуя свойства взаимополярного треугольника. Напишем форму­лу косинуса стороны а' одного из взаимополярных треугольников: cos a' = cos b' cos с' - sin b' sin с' cos A'.

Перейдем к элементам второго треугольника по первому и вто­рому свойствам: а' = 180° — A; b' = 180° — В; с' = 180° — С; A' = 180° — а. Подставив правые части этих равенств в исходную формулу, получим cos (180° — А) = =cos (180° — В) cos (180° — С) + sin (180° — В) sin (180° — С) cos (180° — а), или

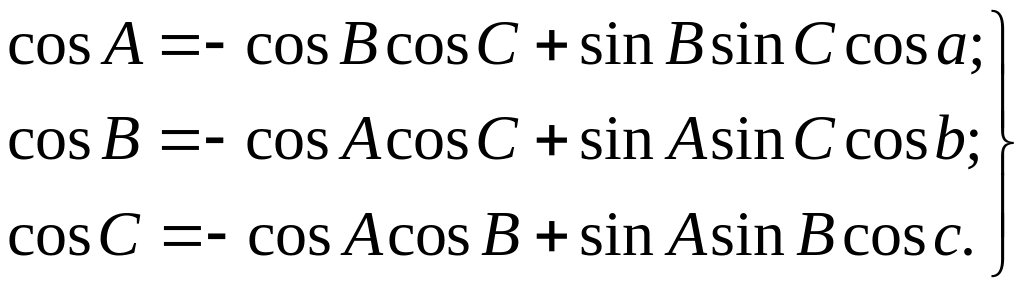
Последние две формулы приведены без вывода. Читается формула косинуса угла следующим образом: косинус угла сферического треугольника равен отрицательному произведе­нию косинусов двух других углов плюс произведение синусов этих уг­лов на косинус стороны между ними (... на косинус стороны, противо­лежащей исходному углу).

Формула синусов (теорема синусов). Эта формула объединяет две стороны и два противолежащих им угла сферического треуголь­ника.

В трехграннике (рис. 2.4) из вершины С опустим перпендикуляр CL на грань АОВ. Из точки L проведем еще две вспомогательные прямые LK и LK': первую — под углом 90° к ребру ОВ, а вторую — под таким же углом к ребру ОА. Соединив точку С с точками К и К', получим два прямоугольных треугольника CKL и CК'L с общим ка­тетом CL, который равен CL = СК sin В в треугольнике CKL; CL = CK' sin A в треугольнике СK'L, т. е.

.

Так как в двух других плоских прямоугольных треугольниках СКО и СК'О стороны СK и СК' являются катетами, то: СК = R sin а; СК' = R sin b. После подстановки в формулу по­лучим R sin a sin В = R sin b sin А, или

.

Здесь последние две формулы составлены по аналогии с первой. Формулы выражают теорему синусов: в сферическом треуголь­нике синусы сторон относятся как синусы противолежащих углов.

Формула пяти элементов. Эта формула объединяет три стороны и два угла сферического треугольника. Выведем ее, пользуясь фор­мулами косинуса сторон а и b:

Подставим в первое выражение значение cos b:

cos a = (cos a cos с + sin a sin с cos B) cos с + sin b sin с  cos А.

Раскрыв скобки и перенеся слагаемые, содержащие cos a, в левую часть, получим cos a (l —cos² с) = sin a sin с cos с  cos B + sin b sin с cos A. Поделим все слагаемые на sin c: cos a sin с = sin a cos с cos B + sin b cos A. Поменяв слагаемые местами, получим формулу пяти элементов: sin b cos A — cos a  sin с — sin a cos с cos B.

Ее читают так: в сферическом треугольнике синус стороны, ум­ноженный на косинус прилежащего угла, равен произведению коси­нуса стороны, противолежащей этому углу, на синус третьей сто­роны минус произведение синуса противолежащей стороны на косинус третьей стороны и на косинус угла между ними.

Так как к каждой стороне треугольника примыкают по два уг­ла — один «слева», другой «справа», то всего можно написать шесть формул пяти элементов:

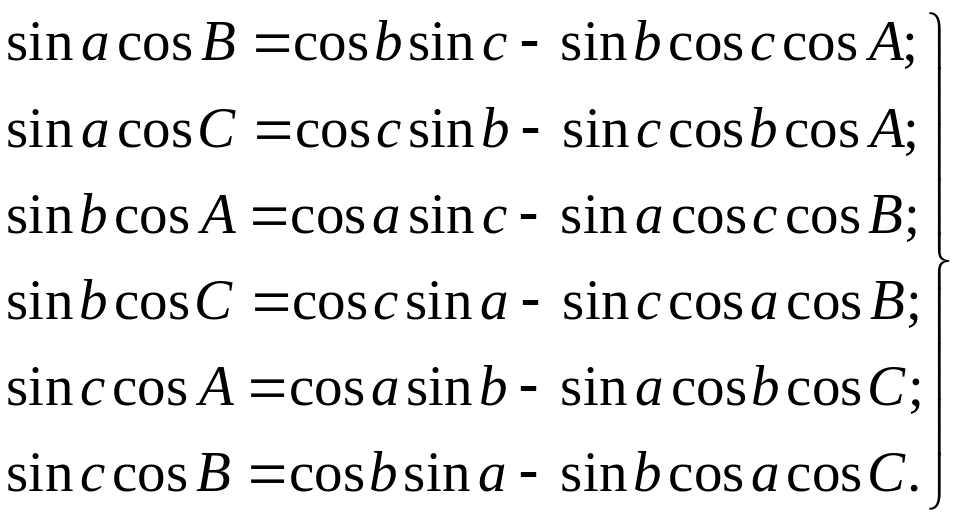
Выведем теперь формулу пяти элементов в другом варианте, когда она связывает три угла и две стороны треугольника. С этой целью напишем две формулы косинуса угла:

Сделаем преобразования, подобные предыдущим:

cos А = -( -cos A cos² C+ sin A cos С sin С cos b) + sin В sin С cos a;

cos A sin² C = -sin A cos С sin С cos b + sin В sin С cos a

и окончательно

sin В cos a = cos A sin C+sin A cos С cos b.

Таким образом, в сферическом треугольнике произведение сину­са угла на косинус прилежащей стороны равно произведению косинуса угла, противолежащего этой стороне, на синус третьего угла плюс произведение синуса противолежащего угла на косинус третьего-угла и на косинус стороны, противолежащей исходному углу.

Таких формул тоже шесть:

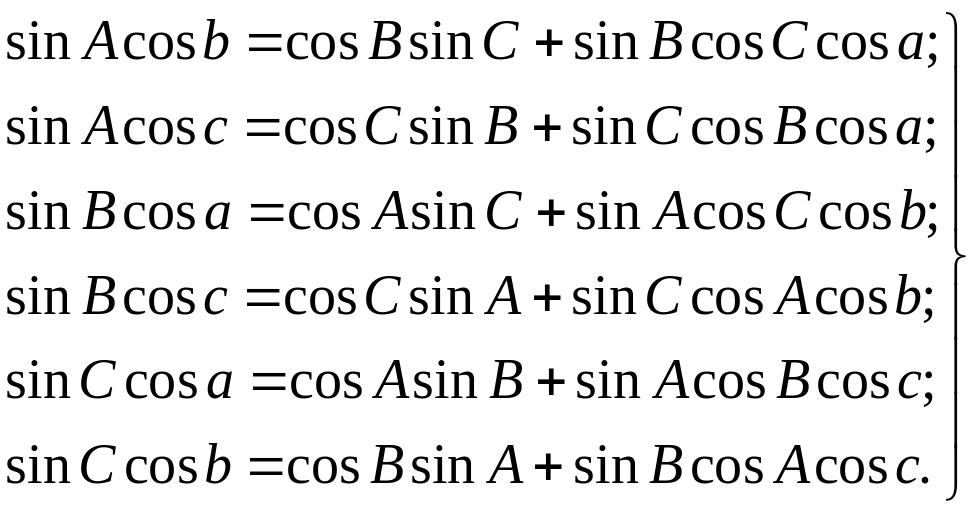
Формула котангенсов (формула четырех рядом лежащих элемен­тов). Эта формула связывает четыре элемента треугольника, распо­ложенных подряд. Для вывода возьмем какую-либо формулу пяти элементов, например

sin b cos A = cos a sin с — sin a cos с cos В.

По теореме синусов выразим величину синуса стороны b:

sin b = sin В sin a/sin A, и подставим ее в начальное выражение:

.

Поделив обе части на sin а, получим ctg A sin B = ctg a sin c - cos с cos В. Это и есть формула четырех рядом лежащих элементов. Выпи­шем объединяемые формулой элементы в том порядке, в каком они даны в треугольнике (рис. 2.4), начиная с угла A и заканчивая сто­роной а: А — с — В — а. В этой формуле элементы (буквы) A и a являются по расположению крайними, а элементы с и В — средни­ми. В связи с этим формулу четырех элементов принято читать так: произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов.

Если от того же крайнего угла A перечислить подряд три эле­мента в противоположном направлении, то по тому же правилу мож­но составить вторую формулу четырех ря­дом лежащих элементов. А так как в ка­честве крайнего может быть любой из трех углов треугольника, то общее число фор­мул котангенсов равно шести: