2. Сферическая тригонометрия

2. а

2. а

1. Основные определения и понятия

Для решения многих задач судовождения используются формулы сферической тригонометрии. На основе таких формул составляют­ся, например, уравнения изолиний и градиентов некоторых нави­гационных параметров, алгоритмы для машинного решения задачи определения места судна; определяются величины углов и сторон параллактического треугольника с целью получения координат ме­ста судна и поправки компаса методами мореходной астрономии.

В навигации формулы сферической тригонометрии применяются, в частности, для расчета дуг больших кругов.

Ознакомимся с терминологией и важнейшими понятиями сфе­рической геометрии и тригонометрии.

Сферой называется замкнутая поверхность, все точки которой равно удалены от одной точки — центра О сферы.

Всякое сечение сферы плоскостью есть окружность. Принято эту окружность называть кругом.

Большим кругом называется след на поверхности сферы, кото­рый образуется при сечении ее плоскостью, проходящей через центр О. Через любую точку поверхности сферы может проходить бесчисленное множество больших кругов, радиус каждого из них равен радиусу сферы. Примерами больших кругов служат меридиа­ны и экватор координатной сетки на поверхности шара.

Полюсом большого круга называется точка поверхности сферы, лежащая на прямой, которая проходит через центр О сферы перпен­дикулярно плоскости большого круга. Каждый большой круг име­ет два полюса Р и Р' (рис. 2.1). Все точки большого круга равноудале­ны от его полюса на величину сферического радиуса.

Сферическим радиусом большого круга является дуга другого большого круга, проходящая от полюса Р (Р') до той или иной точки заданного большого круга. Сферический радиус большого круга равен 90°. На рис. 2.1 показаны сферические радиусы РК и РК'.

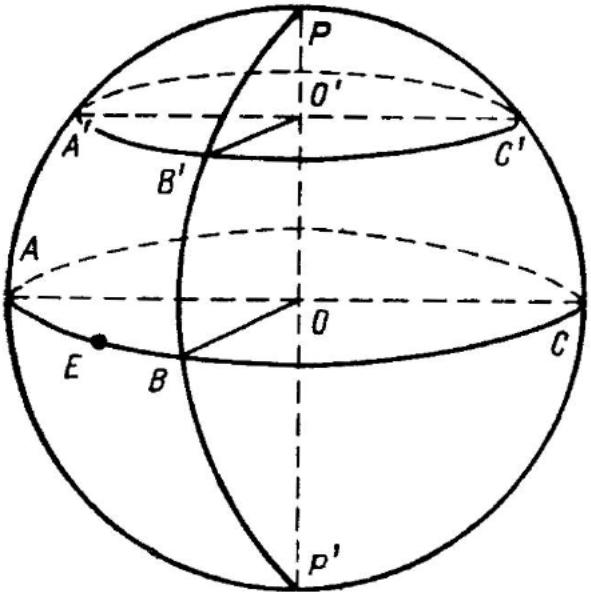
1. Основные линии и точки на сфере

Дуги больших кругов (ДБК) обладают следующими свойствами: положение ДБК определяется двумя точками поверхности сферы (при условии, что эти точки не лежат на концах одного диаметра сферы); ДБК, заключенная между двумя точками сферы, является кратчайшим расстоянием между этими точками.

Из первого свойства следует, что через две точки поверхно­сти сферы можно провести дугу большого круга и причем только одну. Вообще дуга большого круга играет на поверхности сферы такую же роль, как и прямая на плоскости.

Малым кругом называется след на поверхности сферы, образуе­мый в результате сечения ее плоскостью, не проходящей через центр О сферы. К малым кругам, в частности, относятся параллели ко­ординатной сетки шара и круги равных высот светил. Каждый ма­лый круг имеет свои полюсы (Р"). Но сферический радиус малого круга не равен 90°.

Сферическим треугольником называется фигура на сфере, обра­зованная тремя пересекающимися попарно дугами больших кругов. Во всех задачах задаются и определяются элементы такого сфериче­ского треугольника, каждая сторона которого ограничена предела­ми 180° (Эйлеров треугольник).

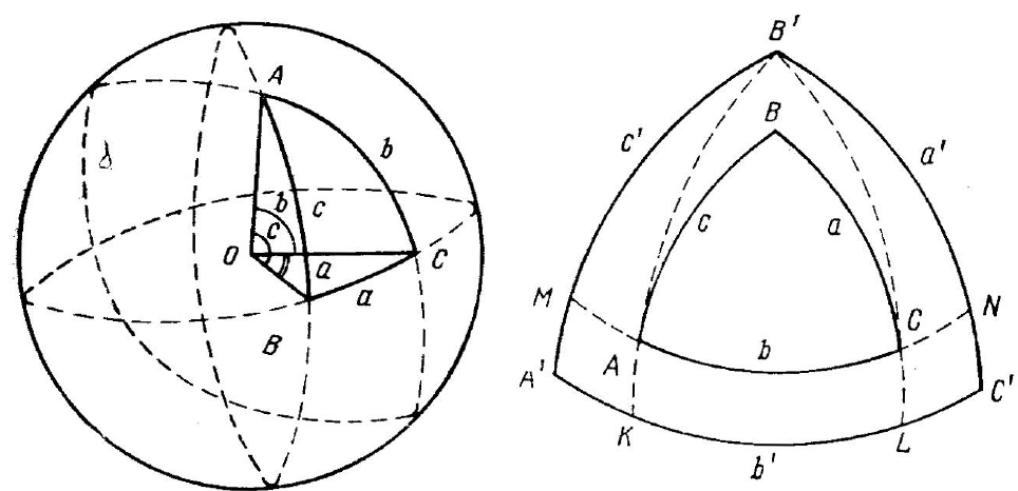
2. Сферический треугольник

3. Взаимно полярные сферические треугольники

На рис. 2.2 показан сферический треугольник с общепринятыми обозначениями его Эл ементов. Углы обозначены прописными бук­вами латинского алфавита А, В, С, а противолежащие углам сто­роны — соответствующими строчными. Точка О обозначает центр сферы и одновременно вершину трехгранника с плоскими углами а, b, с.

Так как длина дуги большого круга выражается произведением центрального угла и радиуса R сферы, то: .

Принимая R = 1, заключаем, что стороны сферического тре­угольника измеряются плоскими углами а, b, с трехгранника. Сумма плоских углов трехгранника и, следовательно, сумма сторон сферического треугольника лежат в пределах

.

Когда сумма сторон становится равной нулю, треугольник пре­вращается в точку, а при a + b + c = 360° — в большой круг. Для сторон сферического треугольника справедливы неравенства вида: а + b > с; а — b < с и т. д.

Углы А, В, С сферического треугольника измеряются двугран­ными углами трехгранника. Так, угол А измеряется двугранным углом при точке О между плоскостями АОС и АОВ трехгранника. Иначе можно сказать, что угол А измеряется углом между каса­тельными AM и AN к сторонам b и с в вершине А треугольника. По свойствам двугранных углов трехгранника сумма углов А, В, С сферического треугольника имеет величину

,

или

.

Здесь выражено основное свойство сферического треугольника, заключающееся в том, что сумма его углов всегда больше 180° на величину сферического избытка (эксцесса) . Величина самого сферического избытка больше 0°, но меньше 360°: 0° <  < 360°. В радианах сферический избыток имеет величину

.

Приведем без доказательств еще некоторые соотношения эле­ментов сферического треугольника:

• сумма двух углов без третьего угла меньше 180°, например: А + В — С < 180°, или А + С — В< 180°;

• против больших сторон треугольника лежат большие углы;

• против равных сторон лежат равные углы;

• площадь сферического треугольника выражается формулой

,

где R — радиус сферы, ед. длины;  — сферический избыток, рад.

Сферические треугольники подразделяются на косоугольные, прямоугольные и четвертные (прямосторонние). У прямоугольного треугольника один из углов равен 90°. Когда у треугольника два прямых угла, он называется двупрямоугольным; возможен и трехпрямоугольный сферический треугольник. У четвертного треуголь­ника равна 90° одна из сторон.

Элементы сферических треугольников в практических зада­чах выражаются в градусной мере, а при рассмотрении теоретиче­ских вопросов — в радианной.