2. Функция в табличном виде

X	y	D
x-1 = 0622’	y-1 = 0,11089	0,00029
x0 = 0623’	y0 = 0,11118
x1 = 0624’	y1 = 0,11147	0,00029
x2 = 0625’	y2 = 0,11176	0,00029

Пример. Требуется найти значение функции у' для аргумента х' = 06°23,4'.

Решение. 1. Вычислим приращение аргумента х относительно бли­жайшего табличного аргумента х₀:

.

2. Для составления пропорции определим шаг таблицы h и разность D табличных значений функции на аргументы х₀ и х₁:

.

3. Составив пропорцию, найдем у:

.

4. Находим искомую функцию у':

у' = у₀ + у = 0,11118 + 0,00012 = 0,11130.

Наряду с линейной применяется также более точная интерполя­ция, называемая квадратичной, или параболической. Она предпо­лагает функциональную зависимость приращений аргумента и функции, геометрически описываемую параболой. Парабола, точ­нее ее участки между узлами интерполяции, лучше, чем прямоли­нейные отрезки, воспроизводит ту кривую, которая представляет заданную функцию у = f (x).

Квадратичная интерполяция выполняется путем расчетов по интерполяционным формулам. В качестве примера здесь приведе­ны две такие формулы, составленные по интерполяционным форму­лам Ньютона и Бесселя:

Формула применяется, если аргумент находится вблизи от начала таблицы, а формула используется, когда аргумент соответствует одному из средних интерполяционных узлов. В этих формулах для краткости введено обозначение U = x/h, остальные обозначения поясняются в табл. 1.3.

3. Обозначения к формулам и

Аргумент	Функция	Разность
		первая	вторая	третья
x-3 = x0 – 3h	y-3
x-2 = x0 – 2h	y-2
x-1 = x0 – h	y-1
x0	y0
x1 = x0 + h	y1
x2 = x0 + 2h	y2
X3 = x0 + 3h	y3

В обозначениях разностей римской цифрой указывается их по­рядок, а в нижнем индексе в условной форме даны номера строк, между которыми данная разность вычислена. Так, обозначение отвечает первой разности значений у₀ и у₁ функции между строка­ми 0 и 1: .

Каждая вторая разность образуется из двух соседних по стро­кам значений первых разностей путем вычитания из большего числа меньшего. Например, . Подобным же образом опре­деляются разности других порядков. Через D_cp в формуле обозначено среднее арифметическое из разностей четного (второго) порядка по соседним строкам: .

Математические таблицы мореходных посо­бий для плавания в основном составлены с такой точностью, что надобности в квадратичной интерполяции не возникает.

Воспользуемся интерполяционной формулой (по Бесселю) для того, чтобы выяснить, при каких условиях можно ограничивать­ся линейной интерполяцией, обеспечивая тем не менее требуемую точность приискания функции. Линейное интерполирование предпо­лагает учет только первых разностей. Это означает, что величины определяются по упрощенной формуле, в которой отброшены все члены более высокого порядка. Так, в формуле для линейной интерполяции надо сохранить только два слагаемых: .

Чтобы первое из отброшенных слагаемых (а значит, и все последующие) не влияло заметно на точность интерполяции, его величина не должна превышать 0,5 единицы последнего десятич­ного знака функции. Применительно к пятизначным математиче­ским таблицам это требование запишется так:

.

Этим именно и определяется условие применения линейной интерполяции. Левая часть неравенства состоит из двух со­множителей. Сомножитель зависит от шага h, выбираемо­го при составлении таблицы. Обозначим этот сомножитель В: 2В = U² — U. Экстремальное значение В_э, при котором выполня­ется условие , найдем, взяв производную и приравняв ее нулю:

, откуда U = ½.

Вторая производная 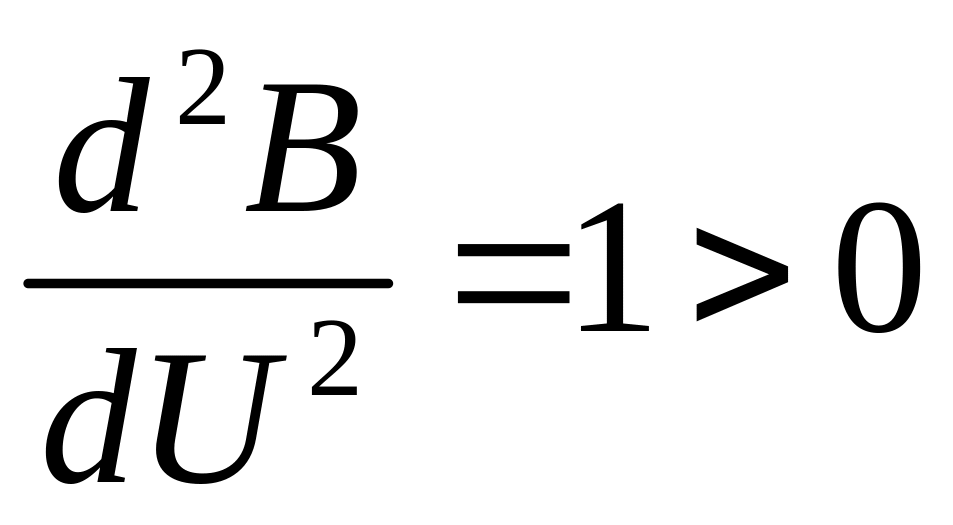показывает, что найден минимум и, следовательно,

.

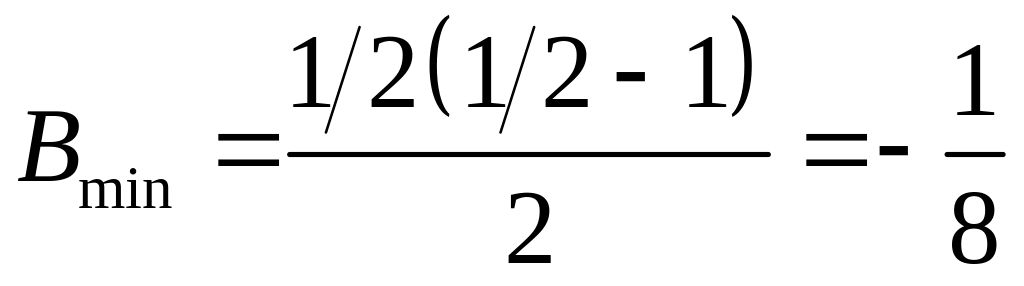Отсюда заключаем, что линейная интерполяция допустима, когда вторые разности не больше четырех единиц пятого десятичного знака: . Указанное условие, как правило, выполняется в мореходных таблицах.

Рассмотрим еще один вид интерполяции — линейную по методу наименьших квадратов. Предположим, что измерениями получено несколько значений функции y₁ = f(x₁); y₂ = f(x₂);…; y_n = f(x_n). Они представлены точками в прямоугольной системе координат. Поставим задачу – найти такую линейную функцию y = ax + b, для которой сумма квадратов отклонений значений функции y = f(x) от значений функции y = ax + b во всех точках с координатами (x_i, y_i) была бы наименьшей:

.

Чтобы при условии найти (и построить) интерполяционную линейную функцию, надо определить величины а и b. Для этого возьмем частные производные от F по а и b и сумму их приравня­ем нулю. После этого путем преобразований получим систему урав­нений

Отсюда и определяются коэффициенты а и b функции у = ах + b. Величина а — угловой коэффициент, выражающий тангенс угла наклона прямой по отношению к положительной оси координат; величина b называется начальной ординатой.