2. Тригонометрические функции малых углов

Один из возможных способов вычисления с заданной точностью той или иной тригономе­трической функции угла  заключается в разложении функции в ряд Маклорена с последующим учетом определенного числа членов разложения:

При малых значениях угла  допустимо ограничиться для рас­чета функции только первыми членами разложения и принять: sin  = ; tg  = ; cos  = 1.

С учетом размерностей эти формулы записываются так:

Наиболее часто применимыми в навигации мерами углов являются градусная, радианная и временная. Для них справедливы следующие соотношения:

.

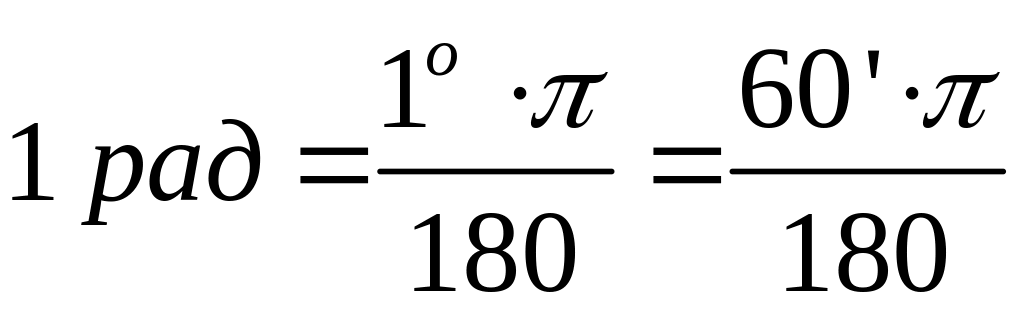Выясним, при каком значении угла  формулы обеспечи­вают определение функций с заданной точностью, например с точ­ностью 0,1’, 1’ или же 6', т. е. 0,1°. Из теории рядов известно, что когда при расчетах ограничиваются каким-либо определенным коли­чеством членов знакочередующегося сходящегося ряда, то связан­ная с этим ошибка результата не превышает первого из отбрасывае­мых членов разложения. Будем считать, что, удерживая в формуле только первый член ряда, мы получим ответ с ошибкой, равной второму члену. Так, полагая sin  = , имеем 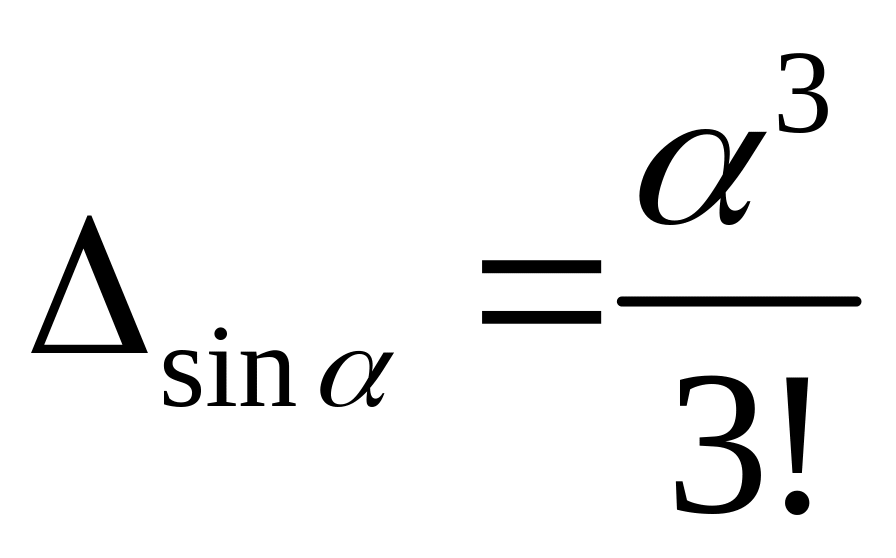, отсюда . Здесь величины  и  даны в радианах. Выразим ошиб­ку  в минутах дуги, а угол  — в градусах: . Подставляя числовые значения, получим: . При  = 1’ получим  = 6,9 =6,9.

Это означает, что заданная точность вычислений ( = 1’) по формуле sin  =  обеспечивается только при угле , равном 6,9° или меньшем указанной величины. Результаты аналогичных вычислений для других тригонометрических функций смотрите в таблице 1.1.

1. Предельные величины аргумента  при заданной точности вычислений тригонометрических функций

Расчетная формула	Предельная величина угла  при допустимой ошибке
	0,1’	1’	6’ (0,1)
sin  = arc 1	3,2	6,9	12,5
tg  = arc 1	2,5	5,5	9,9
cos  = 1	0,4	1,4	3,4

3. Интерполяция

Интерполяцией в вычислительной математике называют способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Интерполяцией пользуются при приближенном решении урав­нений, сглаживании рядов, приближенном интегрировании и в других задачах. В рутинных задачах судовождения интерполяция — вычис­ление значений табулированной функции для промежуточных (меж­ду табличными) значений аргумента.

Предположим, что в табличной форме задана непрерывная функ­ция у = f (х), причем значения функции y_i, y_i+1, …, y_n, соответст­вуют в таблице равноотстоящим значениям x_i, x_i+1, …, x_n аргумен­тов, называемых узлами интерполяции.

1. Линейная интерполяция

Существует несколько видов интерполяции. Наиболее простая из них называется линейной. При линейной интерполяции делает­ся допущение, что коэффициент пропорциональности между прира­щением у функции и приращением х аргумента — величина по­стоянная. На рис. 1.1 функция у=f(х) показана штриховой лини­ей, а отрезки ломаной линии соответствуют линейной зависимости между аргументом и функцией в интервалах x_i+1-x_i, x_i+2-x_i+1 и т. д., которые называются шагом таблицы. Чем меньше шаг h, тем меньше различаются в данном интервале изображающая функ­цию кривая и заменяющая ее прямая линии. Именно с выбором ша­га связаны правомерность линейной (простой) интерполяции и ве­личины сопровождающих ее ошибок.

Пусть аргументу х₀ соответствует величина у₀ функции, ближай­шему к х₀ — меньшему или большему табличному аргументу х₁ — значение y₁ функции. Тогда шаг h таблицы выразится разностью h = x₁-x₀. Разность таблич­ных величин функции обозначим буквой D: D = y₁ - у₀.

Будем искать значение функ­ции у' для аргумента х', нахо­дящегося между табличными аргументами х₀ и х₁, т. е. х₀ < х' < х₁. С этой целью вы­числим величину х = х' — х₀, на которую аргумент х' отли­чается от табличного х₀, а затем составим пропорцию, принимая во внимание, что при изменении аргумента на h функция изменяется на величину D: x/h=y/D (здесь у — разность между приведенной в таблице величиной у₀ и искомым значением у' функции).

Найдя из пропорции величину у: , надо придать ее к табличному значению функции у₀: у' = у₀ + у.

В последней формуле величина у может быть как положи­тельной, так и отрицательной, что зависит от характера изменения функции при возрастании аргумента. Если по мере увеличения ар­гумента х функция у возрастает, величина у положительна; если же аргумент увеличивается, а функция уменьшается, то у отри­цательна. Поясним изложенное примером по данным табл. 1.2.