4. Оптимальный фильтр Калмана

Рассмотренный выше алгоритм последовательного уточнения места судна соответствует процессу фильтрации информации, который называется линейным динамическим сглаживанием или фильтром Калмана.

Рассмотрим вначале одномерный фильтр Калмана. Допустим, в какой-то момент времени Т₁ по нескольким измерениям величины Х определено наиболее вероятное значение . Вес этого значения р₁. Через некоторое время снова произведено однократное измерение этой величины и получено значение х₂. Вес этого значения р₂. При условии независимости и х₂ наиболее вероятное значение на момент Т₂ можно рассчитать по формуле средневзвешенного:

.

Преобразуем эту формулу:

.

Откуда

.

Формула является рекуррентной, т.е. каждое последующее значение вычисляется по той же самой формуле, как и предыдущее. Так, например для момента Т₃ наиболее вероятное значение будет рассчитываться по формуле

.

Запишем формулу в общем виде после нескольких измерений.

.

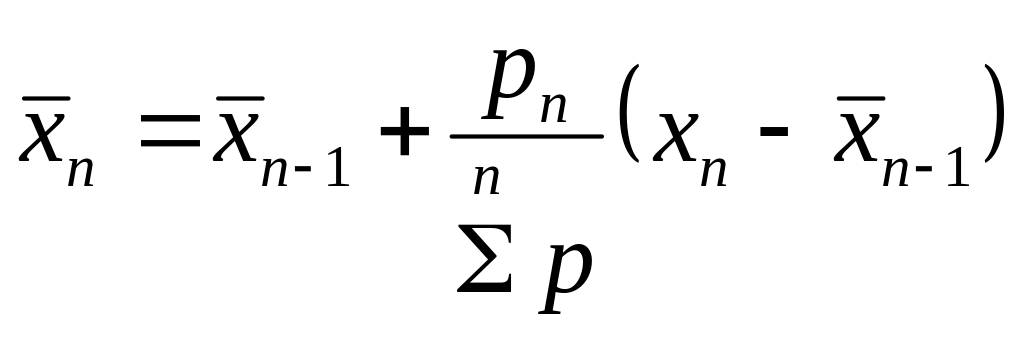Рекуррентное соотношение лежит в основе оптимального фильтра Калмана. Выражение в скобках, разность между результатом последнего измерения и наиболее вероятным значением, имеющимся до этого измерения, называется невязкой. Невязка уточняет имеющееся значение с весом, равным весу последнего измерения.

Дробь, стоящая перед скобками, называется весовым коэффициентом. Обозначим его k_п. Весовой коэффициент показывает, какой вклад вносит измерение в уточнение измеряемой величины. Из этой формулы видно, что с каждым последующим измерением с увеличением суммы весов вклад п − го измерения становится все менее заметным. С одной стороны, это обстоятельство уменьшает влияние случайных погрешностей измерения, с другой стороны, алгоритм становится с каждым уточнением все менее чувствительным к изменению измеряемой величины.

Оценивая точность по формуле , можно записать

Аналогично формуле выводится рекуррентное соотношение для средней квадратической погрешности:

.

Для весового коэффициента также можно записать рекуррентную формулу

.

Таким образом, алгоритм одномерного фильтра Калмана состоит из трех рекуррентных формул:

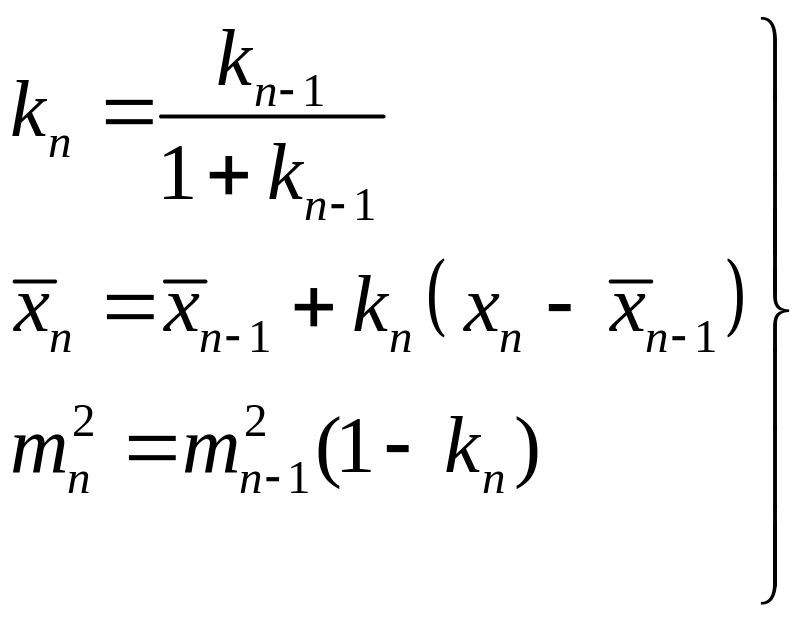
Если измеряемая величина Х изменяется со временем (например, координата движущегося судна), то значение должно быть приведено к последнему моменту. В таком случае говорят о прогнозируемом или счислимом значении . Вес этого приведенного значения за счет погрешностей счисления будет несколько меньше.

Если определяются оптимальные координаты места судна, формулы запишутся следующим образом:

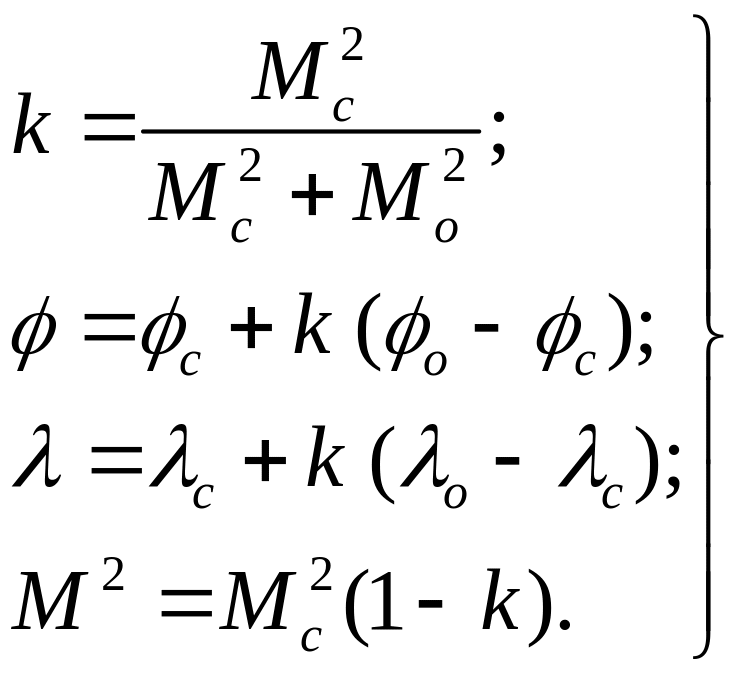
Следует сказать еще об одном источнике увеличения точности определяемых координат. Как уже упоминалось, счислимые координаты содержат погрешности приведения. Эти погрешности могут быть спрогнозированы автокорреляционной функцией на заданном отрезке времени и учтены алгоритмом .