2. Совместный учет счисления и обсервации

Под комплексированием навигационной информации понимается совместная обработка информации, полученной от разных источников, с целью повышения точности результатов. Например, объединение обсерваций, полученных по разнородным навигационным параметрам или объединение счисления и обсервации.

Выше обсервованное место рассматривалось как более точная альтернатива счислимому. Однако при малых интервалах времени между обсервациями погрешности счисления не успевают вырасти и счислимая точка несет информацию, которая не должна отбрасываться. При получении обсервации место должно выбираться с учетом счислимой точки. В этом случае наиболее вероятное место находится как средневзвешенное между счислимым и обсервованным.

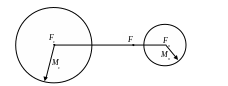
1. Совместный учет счисления и обсервации

Допустим, на какой-то момент времени имеется счислимая F_c и обсервованная F_о точки, СКП которых М_с и М_о (рис. 7.1). Вес счислимой точки , а вес обсервованной точки .

Для нахождения наиболее вероятной точки F расстояние F_c F_о делим на сумму весов и умножаем на вес счислимой точки, а полученный отрезок откладываем от обсервованной точки.

.

Вес наиболее вероятного места равен сумме весов счислимой и обсервованной точек, а его СКП вычисляется по формуле :

.

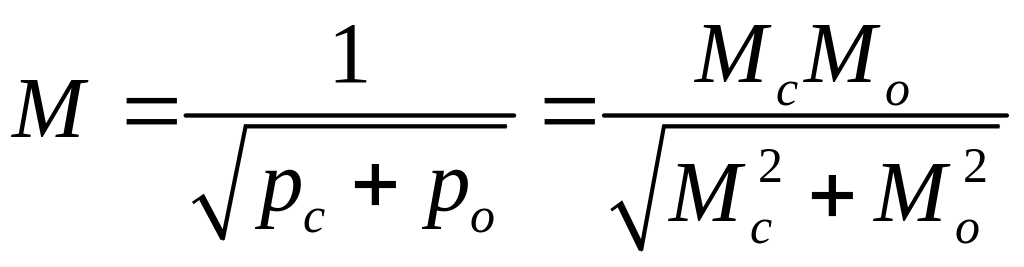Счислимое место может быть уточнено даже измерением одного навигационного параметра, которому соответствует линия положения (лп на рис. 7.2).

В этом случае веса обратно пропорциональны дисперсиям счислимой и определяющей точки по направлению прямой, которая их связывает. СКП по заданному направлению d выражается через полуоси среднего эллипса формулой .

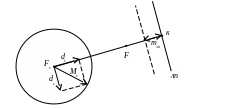
2. Уточнение счислимого места по одной линии положения

Так как точность счислимого места оценивается не эллипсом, а СКП, и ориентировка эллипса неизвестна, приходится брать среднее значение из всех направлений.

Максимальная дисперсия d² вдоль большой полуоси равна а², минимальная − вдоль малой полуоси равна b². Таким образом, средняя дисперсия по любому направлению равна:

.

Заменив числитель по формуле , получим:

.

Формула показывает связь между СКП места судна и осредненную СКП по любому направлению.

Теперь можно рассчитывать веса точек:

Уточненное место F получается вычислением расстояния Fк:

.

СКП уточненного места можно рассчитать по формуле, аналогичной :

.

3. Последовательный метод наименьших квадратов

Если точность счислимого места оценивается эллипсом погрешностей, уточнение счисления линией положения может быть осуществлено более универсальным методом. Суть его в следующем. Допустим в некоторый момент времени в счислимой точке F_c получена линия положения L₁L’₁ (рис. 7.3).

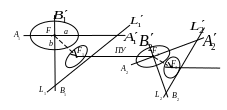
3. Последовательное уточнение места судна

Ее перенос равен р, а направление градиента навигационного параметра − . Точность счислимой точки характеризуется средним эллипсом с полуосями a и b, СКП линии положения − т .

Полуоси эллипса являются экстремальными векториальными погрешностями и, следовательно, он может быть заменен эквивалентными линиями положения А₁А₁' и В₁В₁'. Причем СКП линии положения А₁А₁' равна b, а СКП линии положения В₁В₁' − a.

В

ПУ

результате, в рассматриваемый момент времени имеем три линии положения: А₁А₁' , В₁В₁' и L₁L’₁ . Так как информация поступает от независимых источников, все три линии положения независимые и могут обрабатываться по методу наименьших квадратов для неравноточных линий положения.

Обозначим направление большой полуоси счислимого эллипса через γ. Тогда направление градиента линии положения А₁А₁' будет ₁ = γ + 90^о. Перенос l₁ = 0, так как линия положения проходит через счислимую точку. Вес этой линии положения p₁ = 1/ b². Соответственно, для линии положения В₁В₁' имеем: ₂ = γ, l₂ = 0, p₂ = 1/ а². Для линии положения L₁L’₁: l₃ = l, ₃ = , p₃ = 1/ т².

Таким образом, имеем систему трех неравноточных независимых уравнений линий положения:

Система сводится в систему двух нормальных уравнений, которые решаются как обычно. Параметры среднего эллипса точки F₁ определяются по формулам . Точность точки F₁ за счет третьей линии положения выше, чем F_c. Поэтому ее эллипс погрешностей меньше, чем исходный.

В найденную таким образом точку F₁ переносится счисление и прокладывается путевой угол ПУ.

Через некоторое время получена еще одна линия положения L₂L’₂. Этому моменту соответствует вторая счислимая точка F₂. Эллипс погрешностей этой точки получается сложением эллипса точки F₁ и эллипса погрешностей от счисления (на рис. 7.3 не показан). Погрешности счисления увеличивают эллипс точки F₁ и поворачивают его, так как одна ось эллипса погрешностей от счисления всегда совпадает с линией пути, а другая перпендикулярна ему.

Образовавшийся эллипс погрешностей точки F₂ опять раскладывается на две эквивалентные ему линии положения А₂А₂' и В₂В₂' , которые совместно с линией положения L₂L’₂ обрабатывается методом наименьших квадратов. Получается новая уточненная точка F₃, в которую переносится счисление.

По мере получения новых линий положения процесс повторяется. Причем эта методика может использоваться и при одновременном получении сразу нескольких линий положения. В этом случае линии положения последовательно присоединяются по одной по описанному алгоритму с той лишь разницей, что не будет погрешностей счисления, и эллипс погрешностей с каждой новой линией положения будет уменьшаться.

Если определение места судна выполняется по однородным навигационным параметрам с одной и той же точностью, то с каждым последующим уточнением места вес обсервованной линии положения остается постоянным, а вес линий положения, на которые раскладывается счислимый эллипс погрешностей, увеличивается и, следовательно, уменьшается влияние погрешностей измерения навигационного параметра, происходит их сглаживание.