4. Расчет элементов эллипса погрешностей

Для построения эллипса необходимо знать его большую и малую полуоси (а и b), а также направление большой полуоси а. Параметром, определяющим ориентировку эллипса, является угол φ между более точной линией положения и большой полуосью, который откладывается внутрь острого угла между линиями положения. Эти величины: а, b и φ называются элементами эллипса погрешностей.

Исходной информацией для расчета элементов эллипса погрешностей служат СКП навигационных параметров т. Если в формуле изменение параметра ΔU принять равным т, получим перенос, равный СКП линии положения т_лп:

.

СКП линий положения образуют четырехугольник погрешностей, ограничивающий средний эллипс погрешностей. Для того, чтобы найти зависимость между СКП линий положения и элементами эллипса погрешностей, введем понятие векториальной погрешности.

На рис. 6.5 показан эллипс погрешностей. В произвольном направлении через обсервованную точку проведена прямая АА'. С двух сторон к эллипсу проведены касательные ВВ' и СС', параллельные АА'.

5. Векториальная погрешность

Отрезки от центра до эллипса вдоль прямых АА' и DD' и есть векториальные погрешности. В отличие от вектора векториальная погрешность действует сразу в обе стороны. Векториальные погрешности образуют сопряженные полудиаметры и .

Положения прямой DD', соединяющей точки касания, зависит от положения прямой АА'. Изменив положение прямой АА', изменим и точки касания, т.е. изменится положение сопряженного полудиаметра, изменятся и векториальные погрешности. При вращении сопряженных полудиаметров концы векториальных погрешностей опишут эллипс погрешностей.

В одном из промежуточных положений сопряженных полудиаметров векториальные погрешности будут иметь экстремальные значения, равные полуосям эллипса. На рис. 6.5 они обозначены пунктиром. В другом промежуточном положении сопряженные полудиаметры совпадут с линиями положения, как это показано на рис. 6.6.

Связь между векториальными погрешностями и полуосями эллипса описывается теоремами Аполлония:

С другой стороны зависимость между векториальными погрешностями и СКП линий положения можно определить, построив полосы положения . Полосы положения на рисунке показаны пунктирными линиями. Острый угол между линиями положения обозначен θ.

6. Связь между СКП линий положения и векториальными погрешностями

Векториальная погрешность второго навигационного параметра, действуя вдоль первой линии положения, принимает значение (отрезок АF). Аналогично первая полоса положения на второй линии положения отсекает векториальную погрешность v₁.

Из треугольника АВF имеем

.

Для первой векториальной погрешности можно аналогично записать

.

Учитывая, что θ = Δτ при Δτ ≤ 90^о и θ = 180^о − Δτ при Δτ > 90^о, подставив эти значения в формулы , получим

Удвоим второе равенство в , а затем сложим с первым и вычтем из него:

a ² ± 2 a b + b² = v₁² ± 2 v₁ v₂ sin θ + v₂² .

Из этого следует

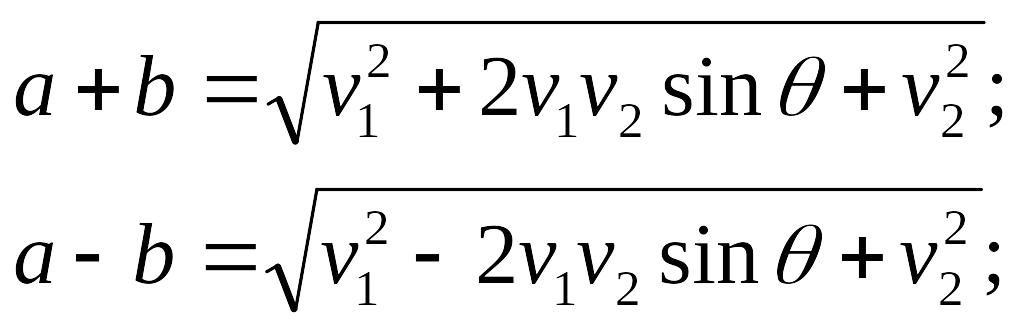
или с учетом и :

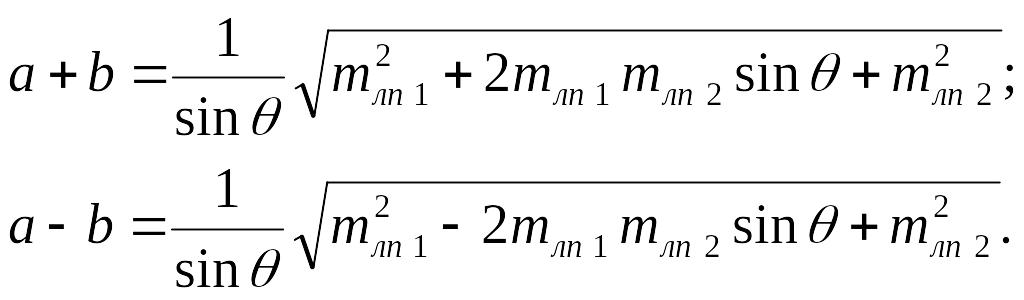
Дальнейший расчет не вызывает затруднений. Полусумма уравнений дает а, а полуразность − b.

Угол φ между более точной линией положения и большой полуосью рассчитывается по формуле

,

где 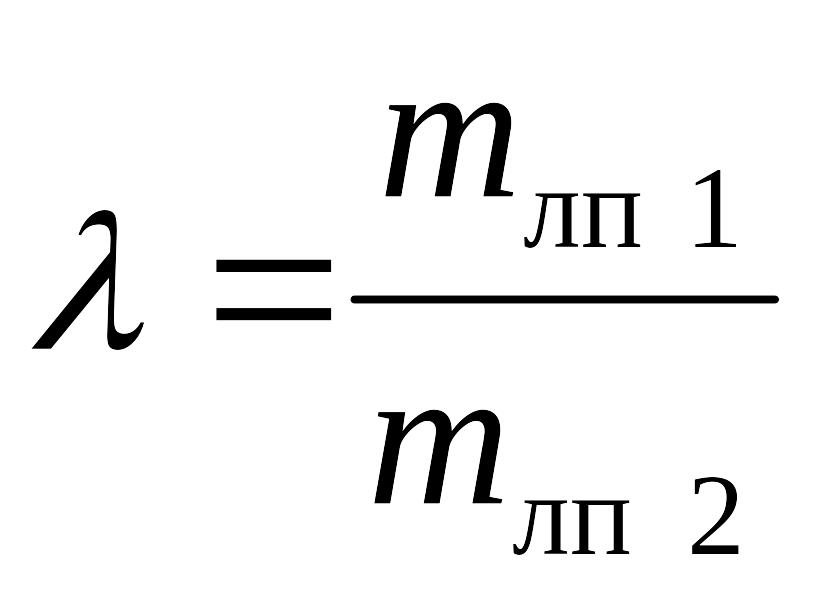, причем индекс «2» присваивается всегда более точной линии положения и дробь всегда больше 1.

Чтобы найти полуоси 95% эллипса, значения полуосей среднего эллипса увеличивают в 2,5 раза:

а _95% = 2,5 а; b _95% = 2,5 b _.

Часто возникает задача не просто ограничить область вероятных мест судна, а узнать, чему равна вероятность погрешности по конкретному направлению. Например, при прохождении узкости необходимо знать, чему равна вероятность того, что погрешность в местоположении судна в боковом направлении (курс ± 90^о) не превысит дистанции до опасной изобаты.

Дисперсия по заданному направлению равна сумме проекций на него квадратов векториальных погрешностей. Полуоси эллипса погрешностей являются частным (экстремальным) случаем векториальных погрешностей. Выразим среднюю квадратическую погрешность d по заданному направлению через полуоси эллипса:

,

где − заданное направление, γ − направление большой полуоси.

Если по формуле вычислить d для различных направлений, отложить по этим направлениям, а потом полученные точки соединить плавной кривой, получим, так называемую, подеру среднего эллипса − геометрическое место точек СКП по направлениям.

На рис. 6.7 эллипс показан пунктиром, а его подера сплошной линией. Отрезок FA − средняя квадратическая погрешность по направлению α.