Эллипс погрешностей
Естественной границей площади, ограничивающей область вероятных мест судна, на первый взгляд кажутся границы полос положения, как это видно на рис. 6.1. Однако более правильным будет проводить границу там, где вероятность местонахождения одна и та же. Наибольшая вероятность в обсервованной точке, и чем дальше от нее, тем меньше эта вероятность.
Чтобы выяснить геометрическую фигуру границы, проходящей через точки равной вероятности, обратимся к рис. 6.4. На нем показана обсервованная точка F и два направления градиентов навигационных параметров, по которым определялось место судна. Вдоль этих направлений действуют случайные погрешности, распределенные по нормальному закону.
Допустим, что действительное место судна находится в точке Z, т.е. была допущена погрешность в первой линии положения х, а во второй − у.
Вероятность того, что будут одновременно допущены погрешности х и у, равна произведению их вероятностей. Геометрически двумерная плотность вероятности представляет собой холмообразную поверхность, показанную на рис. 6.4.
Запишем условие постоянства плотности распределения, заменив в формуле (5.22) средние квадратические отклонения на средние квадратические погрешности, а отклонения от математического ожидания на погрешности х и у:
.
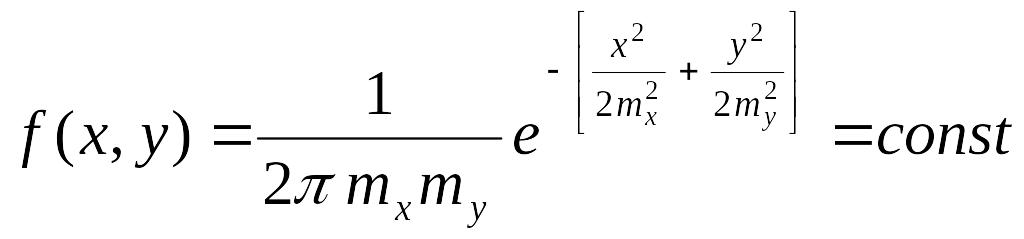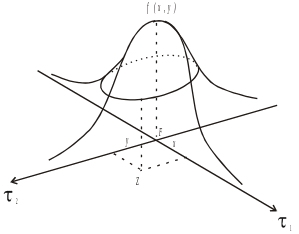
Плотность распределения погрешностей в линиях положения
Геометрически это соответствует сечению поверхности горизонтальной плоскостью.
В формуле переменным является только показатель степени е. Чтобы выполнить условие, надо приравнять показатель константе. Выберем константой величину −с2/2:
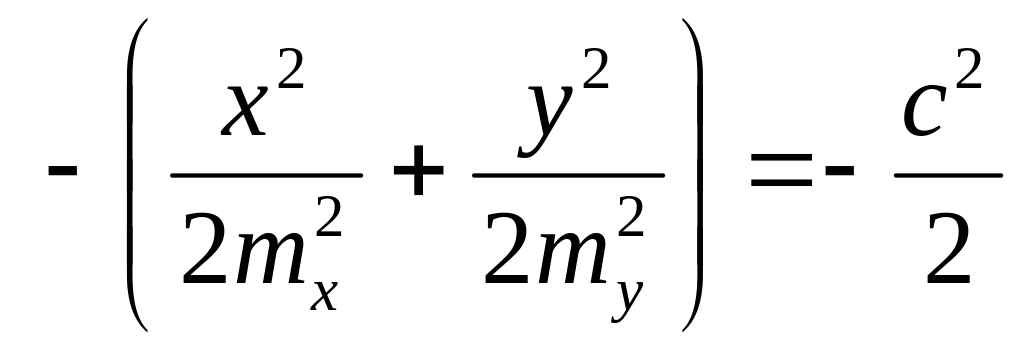
или
.
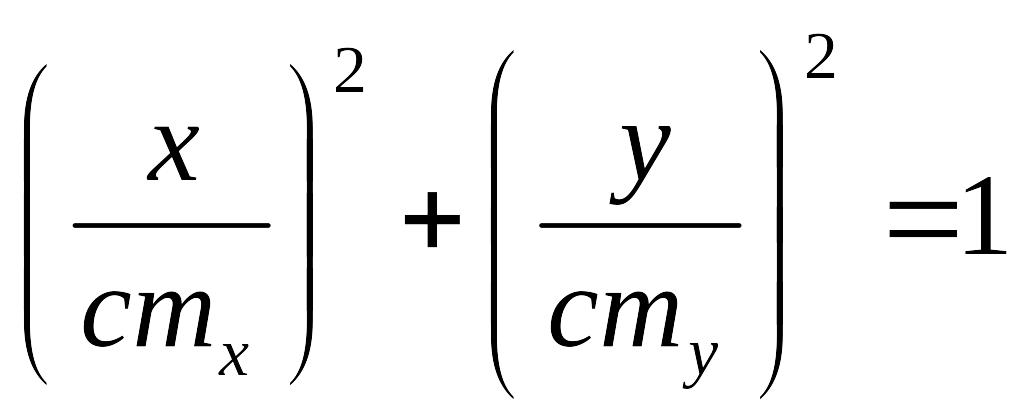Это выражение является уравнением эллипса с полуосями стх и сту.
Таким образом, площадь разброса вероятных мест судна должна ограничиваться эллипсом, который называется эллипсом погрешностей.
Задаваясь различным значением коэффициента кратности с перед СКП линий положения, получим семейство эллипсов с центром в обсервованной точке. Если с = 1, эллипс называется средним эллипсом погрешностей, при с = 2 эллипс называется двойным, при с = 3 эллипс называется тройным или предельным.
Вероятность того, что действительное место судно находится внутри эллипса погрешностей, определяется двойным интегрированием в некоторой области D выражения
.
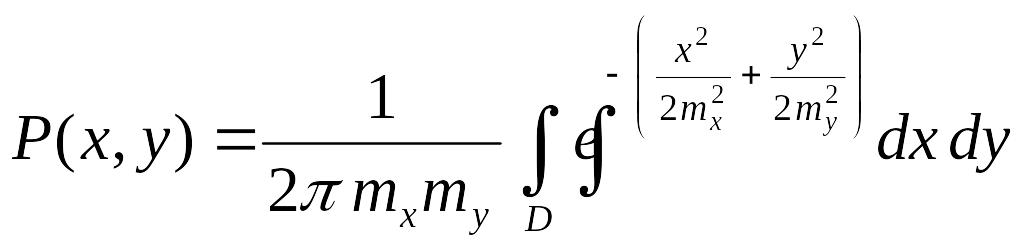Решение имеет вид
.
Подставляя в значения с = 1, 2, 3, получим вероятности нахождения судна в среднем, двойном и тройном эллипсе погрешностей, которые представлены в таблице 6.1.
Вероятности нахождения судна в различных эллипсах
с |
1 |
1,5 |
2 |
2,5 |
3 |
|||||
Р |
0,393 |
0,675 |
0,865 |
0,956 |
0,989 |
|||||
Как видно из таблицы, вероятность того, что судно находится внутри среднего эллипса составляет около 39%. Такая вероятность явно недостаточна. По требованиям Международной морской организации (ИМО), регламентирующей стандарты судовождения, любая фигура погрешностей должна накрывать действительное место судна с вероятностью 95%. Для такого эллипса коэффициент с должен быть равен 2,5. Это означает, что для получения 95% вероятности полуоси среднего эллипса надо увеличить в 2,5 раза.
Оценка точности обсервации эллипсом погрешностей является теоретически обоснованной и полной. Эллипс не только ограничивает область нахождения места судна с любой заданной вероятностью, но и показывает направления максимального (вдоль большой оси) и минимального (вдоль малой оси) разброса вероятных мест относительно обсервованной точки. Из всех возможных фигур погрешностей эллипс обладает наименьшей площадью.