6. Оценка точности места судна

6. А

6. Б

1. Оценка точности обсервации по двум независимым линиям положения

Ранее было рассмотрено определение места судна с помощью изолиний или линий положения по измеренным навигационным параметрам. Если повторяющаяся часть полной погрешности в измеренном навигационных параметрах пренебрежимо мала по сравнению со случайной частью, линии положения считаются независимыми.

Точность обсервованного места зависит от точности измеренного навигационного параметра. Для выяснения этой зависимости выполним графическое построение линий положения, но уже с учетом погрешностей в навигационных параметрах. На рис. 6.1 показана счислимая точка С, обсервованная точка F и две линии положення, которые проходят через определяющие точки к₁ и к₂. Переносы, с помощью которых получены линии положения, имеют случайные погрешности, которые оцениваются СКП − т_лп1 и т_{лп 2} . Это означает, что изображенные на рисунке линии положения являются наиболее вероятными, но могут проходить и в другом месте. Кривые нормального закона распределения также показаны на рисунке. Обсервованная точка получена на пересечении наиболее вероятных линий положения, но в действительности может быть и в другом месте.

СКП линии положения показывает, в каких пределах заключено 68% всех возможных ее положений. Область таких вероятных мест на рис. 6.1 показана пунктиром. Действительная линия положения может проходить и вне этой области, но с вероятностью 32%.

Таким образом, можно утверждать, что с вероятностью 68% судно находится где-то в полосе р ± т_лп. Эта область называется полосой положения. Судоводитель должен полагать, что место судна не на линии, а в полосе положения, притом с вероятностью 68%.

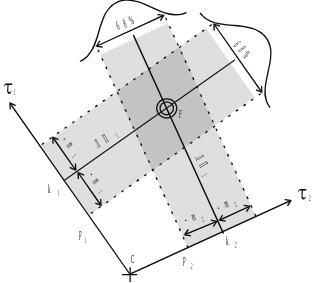
1. Полосы положения

На пересечении линий положения находится наиболее вероятное место, при этом действительное место судна находится не в этой точке, а в некоторой области около нее.

Пересечение полос положения образует четырехугольник, который называется фигурой погрешностей. Она показывает область, в которой с некоторой вероятностью может находиться действительное место судна.

Вероятность того, что действительное место судна находится в этом четырехугольнике, равна произведению вероятностей полос положения, т.е. 0,68² ≈ 0,46 = 46%. Любая обсервация по двум линиям положения имеет свой четырехугольник погрешностей, площадь которого зависит от ширины полос, т.е. от т _{лп 1} и т _{лп 2}. Чем больше СКП линий положения, тем больше площадь разброса вероятных мест судна, но вероятность нахождения внутри каждой такой фигуры одна и та же − 46%. Это дает возможность по величине фигуры погрешностей судить о точности обсервации.

2. Влияние систематической погрешности в линиях положения на обсервованное место

Ранее было рассмотрено определение места судна в предположении о наличии в полной погрешности линии положения случайной составляющей и пренебрежимо малой повторяющейся части. Теперь рассмотрим задачу обсервации, когда повторяющаяся часть полной погрешности явно преобладает над случайной. В таком случае говорят о наличии только систематической погрешности в линии положения.

Допустим, место судна определялось по двум однородным навигационным параметрам. Предположим вначале, что навигационные параметры безошибочны, а линии положения ЛП₁ и ЛП₂, пересекаясь, дают обсервованную точку F, как показано на рис. 6.2.

Если в обоих навигационных параметрах присутствует систематическая погрешность +Δ, она увеличивает переносы пропорционально градиентам на величины

.

Обе линии сместятся по направлению градиентов на Δ₁ и Δ₂ и дадут новую точку пересечения F₁.

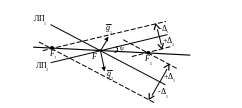
2. Смещение места судна от систематической погрешности

Если систематическая погрешность Δ₂ будет с обратным знаком, линии положения дадут точку пересечения F₂ с другой стороны от истинного места F.

Как нетрудно убедиться из построений на рис. 6.2 все точки пересечения лежат на одной прямой, которая называется линией смещения.

Угол ψ между линией смещения и второй линией положения можно получить, рассматривая зависимости сторон в треугольниках на рис. 6.2. Этот угол равен

,

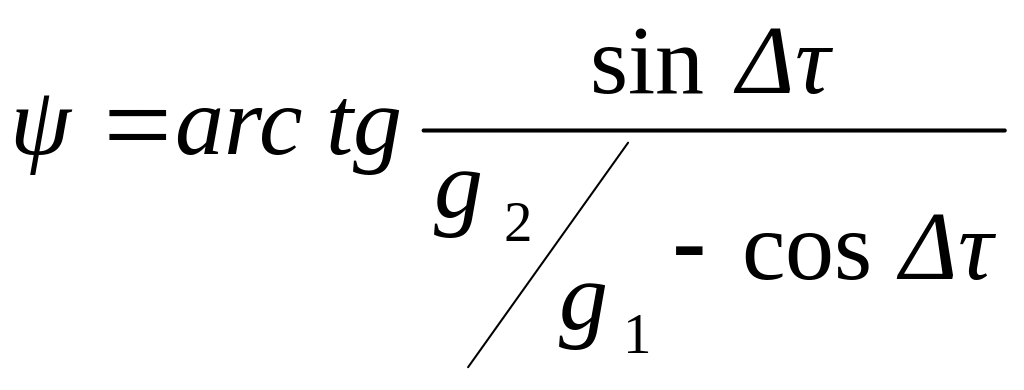где Δτ − угол между направлениями градиентов.

В формуле нет смещений Δ₁ и Δ₂ , т.е. положение линии смещения не зависит от величины и знака систематической погрешности в навигационном параметре, и место судна всегда будет располагаться на этой прямой.

Если градиенты параметров одинаковы (например, для высот светил), выражение упрощается:

.

Это означает, что линия смещения пойдет по биссектрисе угла между градиентами, которая называется астрономической биссектрисой.

Следует особо отметить, что смещается обсервованная точка именно по биссектрисе угла между градиентами, а не острого угла θ между линиями положения, как может показаться на первый взгляд. Чтобы убедиться в этом, рассмотрим рис. 6.3.

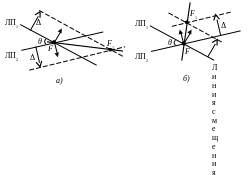
3. Астрономическая биссектриса

На нем показаны две одинаковые высотные линии положения, смещенные под действием систематической погрешности Δ. Но на рис. 6.3 б) градиент второй высоты светила имеет противоположное направление. Таким образом, при наличии систематической погрешности в линиях положения место судна определить нельзя, а только линию смещения, на которой оно находится, в частном случае на астрономической биссектрисе.

Уравнения двух линий положения, в которых присутствует систематическая погрешность Δ, выглядит следующим образом:

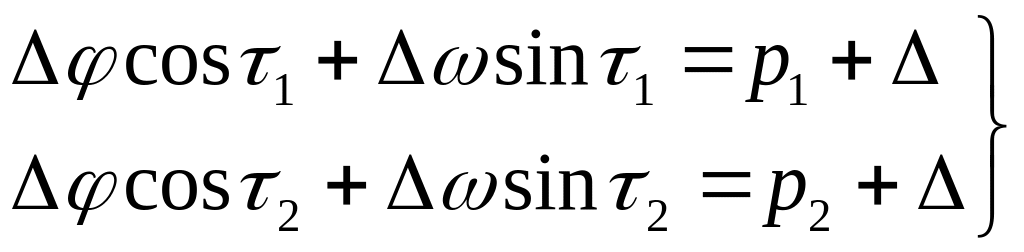
Чтобы избавиться от систематической погрешности, вычтем из первого уравнения второе:

Δφ (cos τ₁ − cos τ₂ ) + Δω ( sin τ₁ − sin τ₂ ) = р₁ − р₂ .

Формула является уравнением астрономической биссектрисы между первой и второй линиями положения. В этом уравнении два неизвестных Δφ и Δω. Чтобы определить место судна нужно уравнение второй биссектрисы. Для этого нужна третья линия положения, которая позволит записать уравнение второй биссектрисы:

Δφ (cos τ₁ − cos τ₃ ) + Δω ( sin τ₁ − sin τ₃ ) = р₁ − р₃ .

Система уравнений и свободна от систематической погрешности и решается, как обычно, относительно Δφ и Δω. Подставив эти значения в уравнение любой линии положения, можно найти и систематическую погрешность Δ. Идентичное решение будет, если вместо записать разностное уравнение второй и третьей линии положения. Третья биссектриса с неизбежностью пройдет через обсервованную точку. Заметим, что третья линия положения не будет избыточной, так как определяются три неизвестных: Δ, Δφ и Δω.

Описанный прием исключения систематической погрешности в линиях положения в графическом варианте путем построения биссектрис используется в мореходной астрономии.