5. Градиент навигационного параметра

Уравнения линии положения в виде можно использовать в аналитическом решении. Однако для построения линии положения на карте от счислимой точки необходимо знать, на сколько должна сместиться линия положения (или изолиния) при изменении навигационного параметра на ΔU.

Это смещение обозначим буквой р. Оно пропорционально изменению навигационного параметра, а коэффициент пропорциональности g называется градиентом навигационного параметра:

ΔU = g р.

Отсюда выразим градиент

.

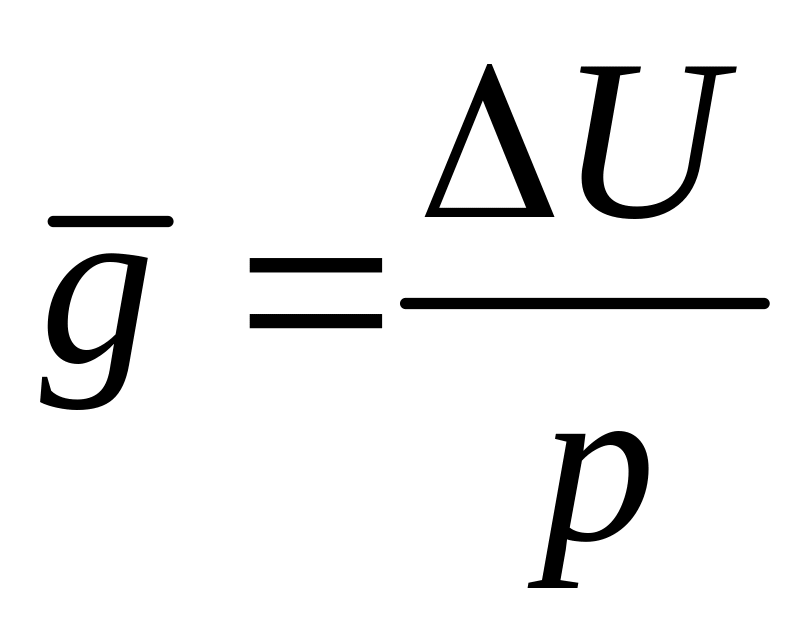При перемещении точки по земной поверхности значение навигационного параметра в ней изменяется по-разному, а вдоль изолинии − вообще не меняется. Максимального значения изменение навигационного параметра достигает при перемещении точки перпендикулярно к изолинии. Поэтому градиентом навигационного параметра называется векторная величина, характеризующая скорость изменения навигационного параметра при перемещении по нормали к изолинии в сторону увеличения параметра.

На рис. 5.3 показана изолиния, проходящая через счислимую точку С и градиент , проходящий перпендикулярно к ней.

Как любая векторная величина, градиент характеризуется модулем g и направлением τ. Разложим по осям и обозначим проекцию градиента на меридиан g_φ , а проекцию на параллель − g_ω. Как видно из рис. 5.3, если характеризует скорость изменения параметра по нормали к изолинии, то g_φ характеризует скорость изменения параметра вдоль меридиана, т.е.

.

Соответственно g_ω характеризует скорость изменения навигационного параметра при перемещении по параллели:

.

3. Градиент навигационного параметра

Из построений на рис. 5.3 следует, что

.

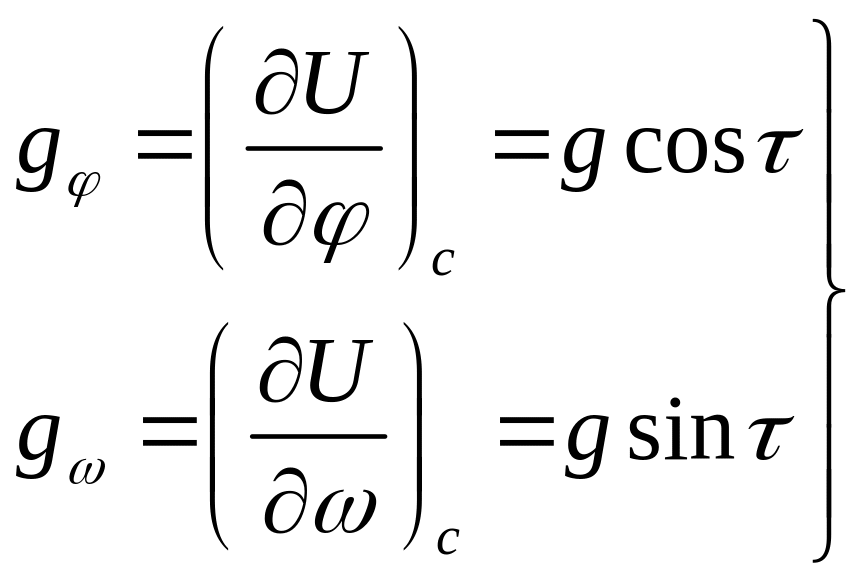Формулы позволяют определять как модуль градиента навигационного параметра, так и его направление через частные производные навигационной функции. Возведя в квадрат каждое уравнение и сложив, найдем квадрат модуля, откуда, извлекая квадратный корень, получим

.

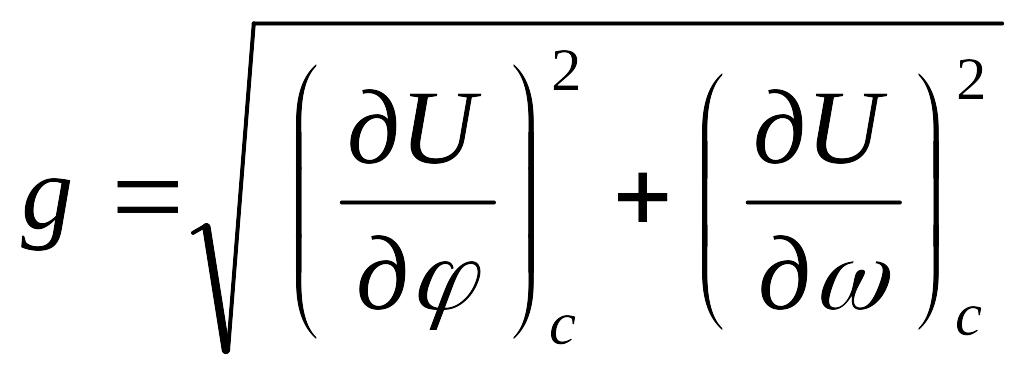Поделив второе уравнение на первое, найдем тангенс направления градиента

.

По формулам и можно вычислить модуль и направление градиента любого навигационного параметра, если известна его навигационная функция.

Расстояние. Приращение расстояния D обусловливает такое же смещение р изолинии и поэтому модуль градиента расстояния g_D = 1. Направлен этот градиент от ориентира, т.е.  = П +180. (С - судно, А – мыс).

Высота светила. Приращение высоты h вызывает такое же уменьшение зенитного расстояния Z, которое равно расстоянию до полюса освещения. Поэтому модуль градиента высоты светила такой же, как и расстояния: g_h = 1, а направлен градиент к светилу, т.е.  = А, где А – азимут светила.

Пеленг на плоскости. На рис. 5.4 показано смещение места р при изменении пеленга на ΔП , градиент направлен в сторону возрастания пеленга, место судна обозначено буквой С, ориентир − А.

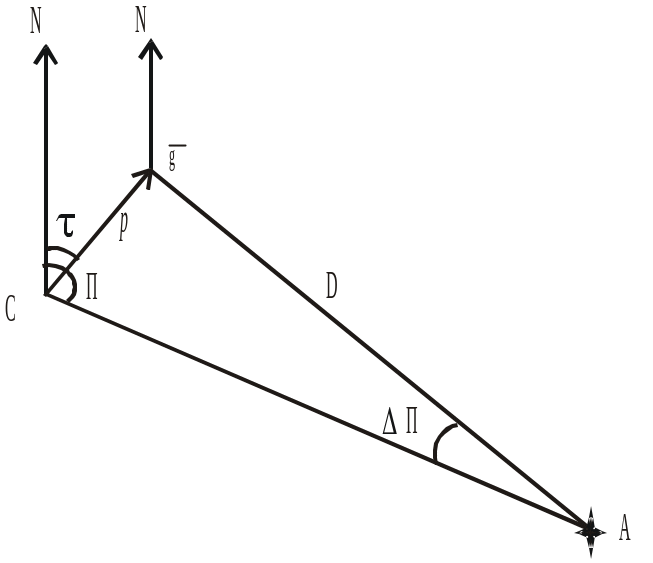
4. Градиент пеленга на плоскости

Модуль градиента определяется формулой . В данном случае ΔU = ΔП. Из треугольника СА: р = D sin ΔП или (по малости угла ΔП) р = D ΔП. Подставив в выражения ΔU и р, получим

.

Из рис. 5.4 следует: τ = П − 90^о.