Обобщенный метод линий положения
Определение места судна по изолиниям имеет существенные недостатки. Графическое решение возможно только для простых изолиний − окружностей и прямых линий. К тому же, если ориентир находится за рамкой карты, такое построение невозможно или требует дополнительных вычислений.
Аналитическое решение тоже затруднено, так как многие изолинии описываются трансцендентными уравнениями (решение которых не выражается алгебраическими корнями). Система трансцендентных уравнений обычно решается методом итераций. В редких случаях можно получить аналитическое решение путем сложных преобразований самих уравнений.
Кроме того, любые две изолинии (кроме прямых) дают более одной точки пересечения. Для устранения неоднозначности решения необходимо привлекать дополнительную информацию. Обычно такой информацией являются координаты счислимой точки.
Указанных недостатков можно избежать, если определять место судна обобщенным методом линий положения, который был предложен В.В.Каврайским в 1920 году. Суть метода заключается в том, что отрезки изолиний в окрестности счислимой точки заменяются касательными. Такая касательная к изолинии вблизи счислимой точки называется линией положения.
Касательная − это прямая независимо от формы изолинии. Поэтому метод называется обобщенным. Две прямые пересекаются в одной точке, что делает решение однозначным. Линия положения строится относительно счислимой точки независимо от того, находится ориентир на карте или нет. Значительно упрощается также аналитическое решение, которое сводится к решению унифицированной системы двух линейных уравнений с двумя неизвестными.
Чтобы получить уравнение касательной к изолинии, надо навигационную функцию разложить в ряд Тейлора, ограничившись линейными членами разложения:
.
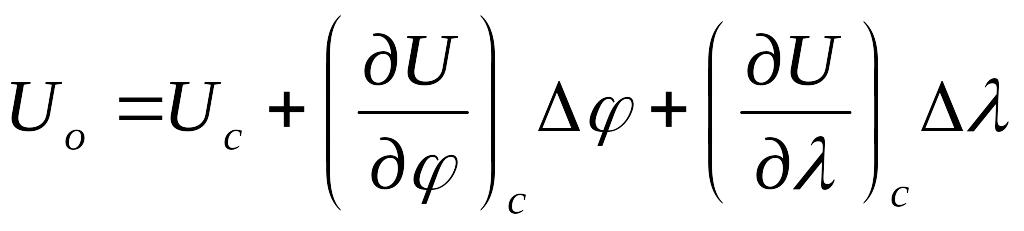Здесь индекс «о» означает обсервованное (измеренное) значение, индекс «с» − счислимое значение.
Уравнение представляет собой уравнение прямой в системе координат, осями которой являются меридиан и параллель, а начало отсчета находится в счислимой точке. Чтобы уравнять масштабы по осям этой системы, надо разность долгот перевести в отшествие, для чего последнее слагаемое в умножим и разделим на cos φс. С учетом этого формулу можно представить в виде
,
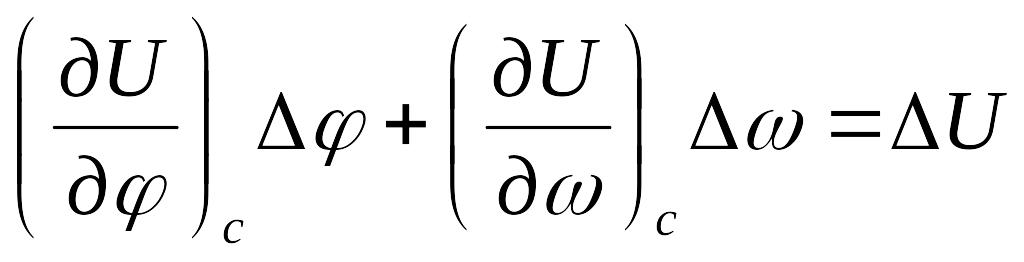где
−
разность значений навигационного
параметра в обсервованной и счислимой
точке,
− разность широт между обсервованной
и счислимой точками,
−
отшествие между обсервованной и
счислимой точками.
Физический смысл частных производных следующий:
− скорость изменения навигационного
параметра вдоль меридиана,
−
скорость изменения навигационного
параметра вдоль параллели,
Для двух навигационных параметров можно составить систему двух уравнений линий положения
,
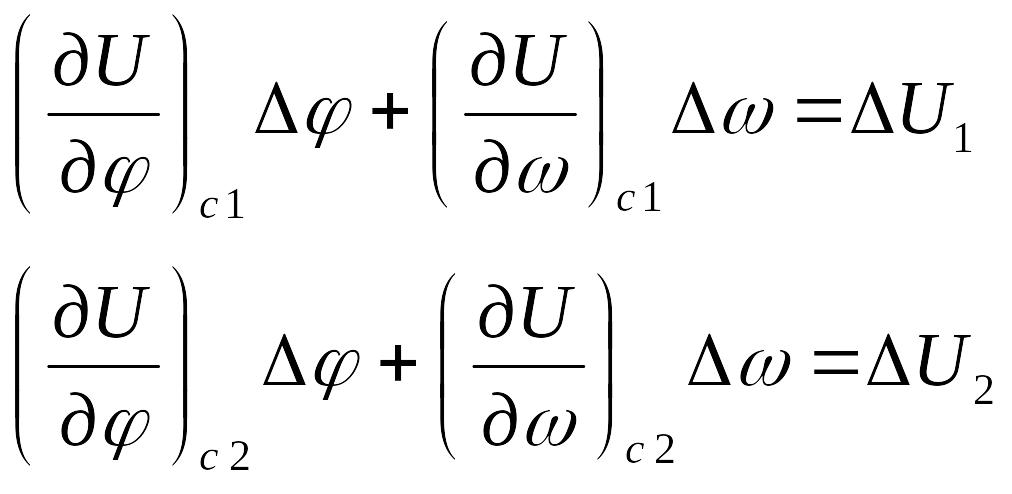
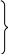которая решается относительно Δφ и Δω. Затем рассчитываются обсервованные координаты:
.
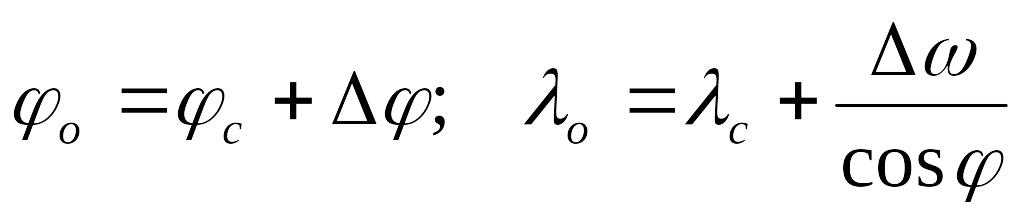Обобщенный метод линий положения имеет некоторые принципиальные отличия от метода изолиний. Во-первых, используются счислимые координаты в навигационных функциях, а не обсервованные. Во-вторых, применение касательных вместо изолиний вносит методическую погрешность в обсервованные координаты, так как действительное место на пересечении изолиний, а не касательных. Однако этими погрешностями при невязках менее 30 миль можно пренебречь. В-третьих, определяются не сами координаты, а их приращения к счислимым.