Навигационные параметры
Для обеспечения безопасности во время перехода судоводитель должен постоянно контролировать место судна. По путевому углу и пройденному расстоянию на любой момент времени можно вычислить местоположение судна. Такой способ определения места судна называется счислением, а само место − счислимым.
Из-за погрешностей в направлении движения и пройденном расстоянии с течением времени счислимое место становится все более неопределенным и возникает необходимость его уточнения. Сделать это можно относительно ориентиров, положение которых хорошо известно. Определение места судна по ориентирам называется обсервацией, а место, полученное таким образом, − обсервованным. Ориентиры могут быть естественными (мысы, горы, скалы, небольшие островки) или искусственными, специально созданными для целей судовождения (маяки, башни, створные знаки). Ориентирами являются не только объекты на земной поверхности, но также искусственные спутники Земли и небесные светила.
Определение места судна по известным координатам ориентиров является геометрической задачей. Для ее решения используются различные геометрические величины, связывающие координаты ориентиров с координатами точек на земной поверхности. Эти величины называют навигационными параметрами. Примеры навигационных параметров: пеленг на ориентир или обратный пеленг, дистанция до ориентира, вертикальный угол, горизонтальный угол между двумя ориентирами, высота светила, разность расстояний до двух ориентиров и т.д.
Аналитическая зависимость навигационного параметра от координат на земной поверхности называют навигационной функцией U.
где U − значение параметра; φ и λ − координаты судна
Для получения значений навигационного параметра созданы приборы и системы, с помощью которых измеряются различные физические величины, определенным образом зависящие от взаимного расположения ориентира и судна. Для этого могут использоваться электромагнитные, акустические, геомагнитные, гравитационные поля. При этом измеряются: направление лучей, частоты, фазы и амплитуды радиосигналов, интервалы времени распространения сигналов или их разность и т.п.
Рассмотрим навигационные функции основных навигационных параметров.
Дистанция на плоскости
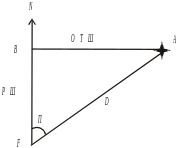
На небольших расстояниях земную поверхность можно принять за плоскую. На рис. 5.1 показаны ориентир А и судно F. Дистанцию D можно определить по теореме Пифагора, где катетами служат разность широт и отшествие:
.
где
и
−
координаты судна;
а и а− координаты ориентира;
ср − средняя широта между судном и ориентиром.
Пеленг и дистанция
Вертикальный угол на плоскости
Пеленг на плоскости
Из треугольника АВF (рис. 5.1)
.
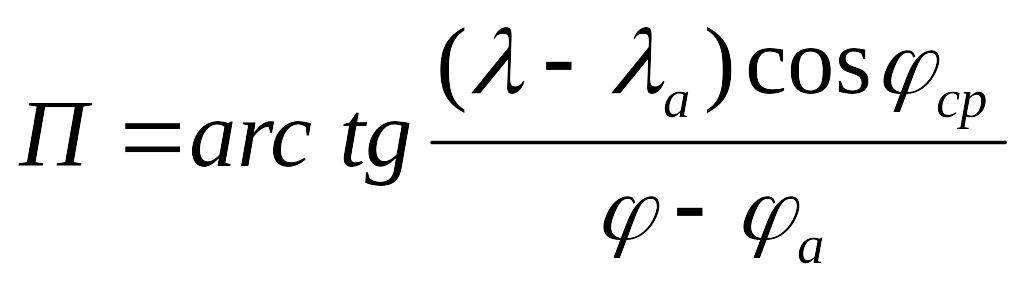Вертикальный угол
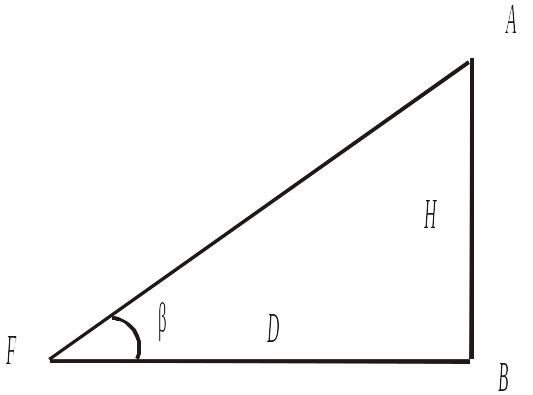
Если измерен вертикальный угол какого-либо ориентира, высота которого Н известна (например, маяка или башни), то из треугольника АВF (рис. 5.2) можно найти катет ВF − дистанцию до ориентира
.
Подставив сюда выражение для дистанции из , получим
.
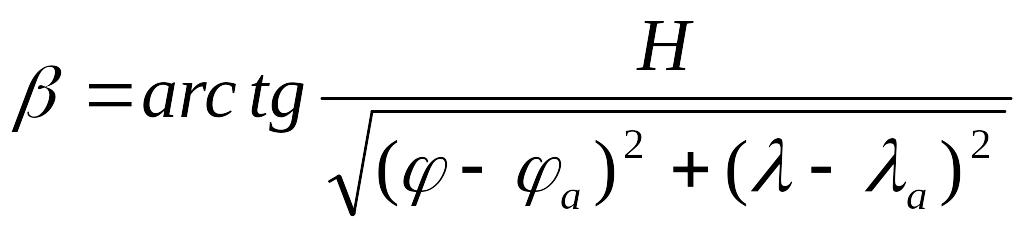Дистанция на сфере
В разделе 2 была получена формула , с помощью которой рассчитывается расстояние между двумя точками на сфере (длина дуги большого круга). Приняв точку В за ориентир, а точку А за место судна, получим навигационную функцию для дистанции на сфере
Пеленг на сфере
В том же разделе получена формула (2.11) для начального курса плавания по ортодромии. Так как эта формула показывает связь между координатами двух точек с направлением из одной точки на другую, то приняв точку В за ориентир, а точку А за место судна, получим навигационную функцию для пеленга на сфере
.
Высота светила
Для нахождения навигационной функции высоты светила воспользуемся формулой . Эта формула показывает зависимость высоты светила от координат светила, часового угла t и склонения δ, а также широты места судна φ. В свою очередь часовой угол является алгебраической суммой гринвичского часового угла и долготы места судна.
С учетом этого формулу (2.13) можно записать в виде
.