5. Оценка точности функции измеренных аргументов

Если результат измерения, отягощенный погрешностью, используется для вычисления какой-либо функции, то и функция получается с погрешностью. Точность функции оценивается средней квадратической погрешностью. В общем случае функция зависит от нескольких аргументов и погрешности каждого искажают вычисленное значение функции.

Выясним зависимость СКП функции от СКП аргументов. Допустим, задана функция

z = f (x, y…) .

Было произведено п измерений аргументов, по которым рассчитывается значения функции z. Обозначим погрешности в аргументах через x, у и т.д., а погрешность функции − z. Тогда каждому измерению будет соответствовать уравнение

z + z_i = f (x + x_i , y + у_i …) .

Разложим правую часть в ряд Тейлора, ограничившись линейными членами, и вычтем из полученного равенства

.

Чтобы перейти от индивидуальных погрешностей к средним квадратическим, возведем равенство в квадрат, просуммируем все п уравнений и разделим на п – 1:

.

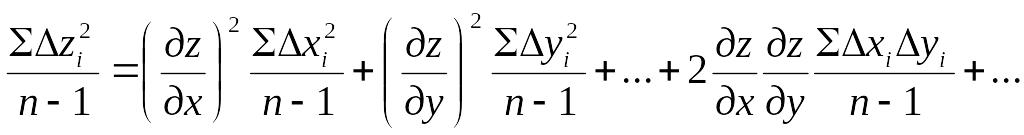Суммы квадратов погрешностей, деленные на п – 1, представляют собой квадраты СКП переменных, а суммы в слагаемых с коэффициентом 2 − корреляционные моменты соответствующих аргументов:

.

Извлекая квадратный корень из обеих частей равенства , получим общую формулу СКП функции измеренных аргументов

.

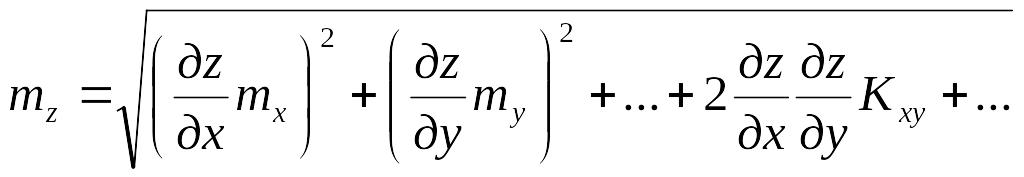Формула используется для взаимозависимых аргументов. Если аргументы независимы, корреляционные моменты становятся равными нулю и СКП функции рассчитывается по формуле

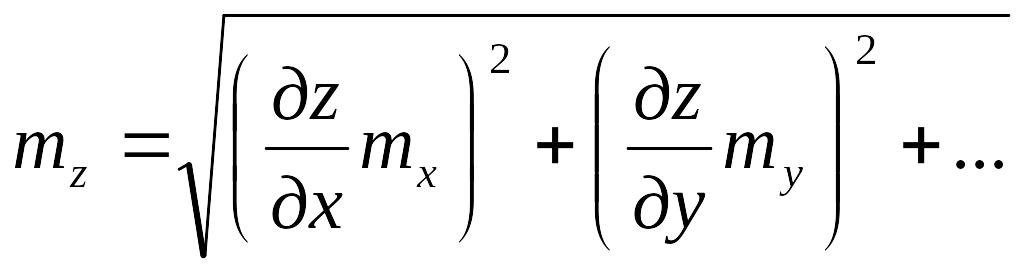
Таким образом, чтобы оценить СКП функции, надо определить ее частные производные по всем аргументам, содержащим погрешности и умножить их на СКП этих погрешностей.

Большинство формул, используемых в судовождении, являются одночленными выражениями, При их дифференцировании для нахождения частных производных полезно использовать следующий прием.

Если функция задана в виде

z = Ах^ту^п, то ; .

Этот прием применим при любом количестве сомножителей, любых, в том числе отрицательных и дробных показателях степеней. Он позволяет значительно облегчить вычисления производных. При этом, что важно, при подстановке производных в формулу размерности переменных сокращаются с размерностями соответствующих СКП. Таким образом, размерность СКП функции получается одинаковой с размерностью самой функции.

Порядок вычислений СКП функции следующий.

1. Вычислить значение самой функции.

2. Вычислить частные производные функции по всем переменным.

3. Подставить найденные значения вместе с СКП в формулу .

4. Привести в соответствие друг другу размерности слагаемых под радикалом. На это следует обратить особое внимание, так как именно из-за этого происходят, в основном, ошибки в вычислениях.

5. Выполнить вычисления.