3. Обработка измерений навигационных параметров

Навигационным параметром называется геометрическая величина, связывающая координаты ориентиров с координатами точек на земной поверхности.

Измерения взаимозависимые и неравноточные

Для получения значения навигационного параметра достаточно одного измерения. Чтобы уменьшить влияния случайных погрешностей, делается серия измерений.

Допустим, измерена серия какого-либо навигационного параметра Х и после исправления поправками получены результаты х₁, х₂…. х_п. Измерения не равноточные. Точность каждого измерения оценим полной средней квадратической погрешностью (СКП) т_i. Обозначив искомое значение навигационного параметра через х_о, для каждого измерения можно записать уравнение

х_о  х_i.

В каждом результате измерения содержится полная погрешность V_i, состоящая из случайной и повторяющейся части. Чтобы получить точное значение навигационного параметра, эту погрешность из результата измерения надо вычесть:

х_о = х_i− V_i.

Таким образом, для п измерений будем иметь систему п уравнений вида

V_i = х_i− х_о,

которые называются уравнениями невязок.

Наиболее вероятное значение х_о будем искать в соответствии с принципом максимального правдоподобия. Для этого надо, чтобы совокупность невязок обладала наибольшей плотностью вероятности.

Обратимся к формуле представляющей плотность вероятности для системы произвольного количества случайных величин. В ней выражение, стоящее перед основанием натурального логарифма е, для данной совокупности − константа. Невязки входят в показатель степени:

.

Чтобы плотность вероятности была максимальной, надо отрицательный показатель степени е минимизировать, т.е. значение х_о надо выбрать таким, чтобы

.

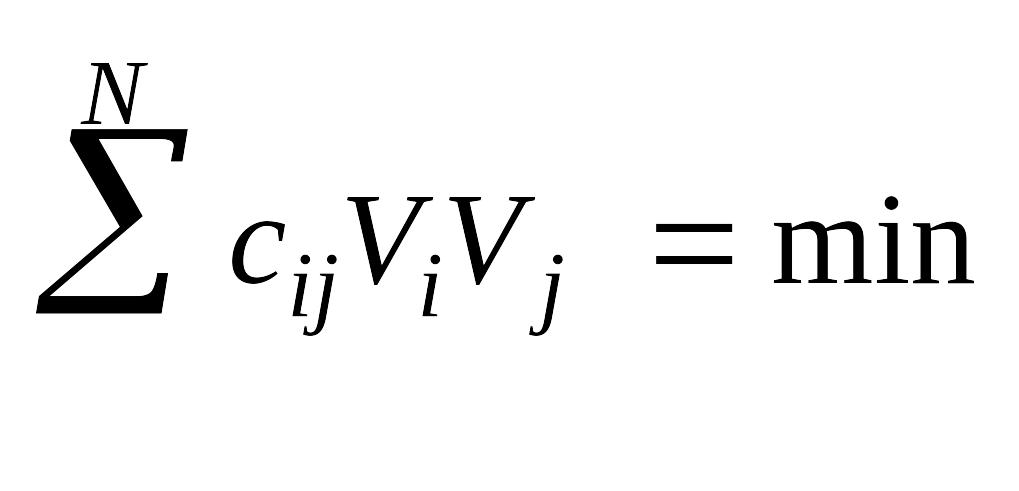Левая часть − однородный многочлен второй степени относительно невязок, называемый квадратичной формой. Поэтому метод определения неизвестного значения случайной величины наложением условия называется методом наименьшей квадратичной формы или обобщенным методом наименьших квадратов.

Для нахождения минимума необходимо производную функции приравнять к нулю. Подставив в выражения для невязок из , можно записать

.

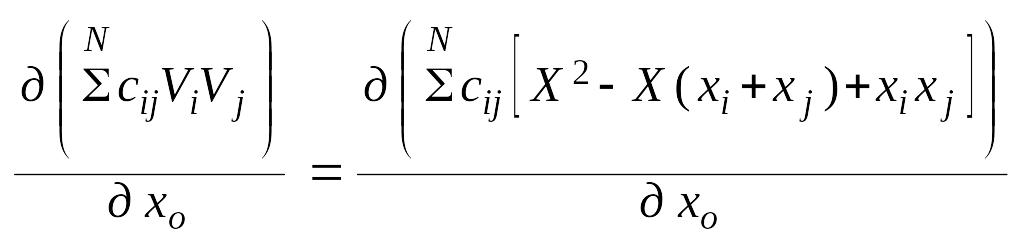Произведя дифференцирование, получим

.

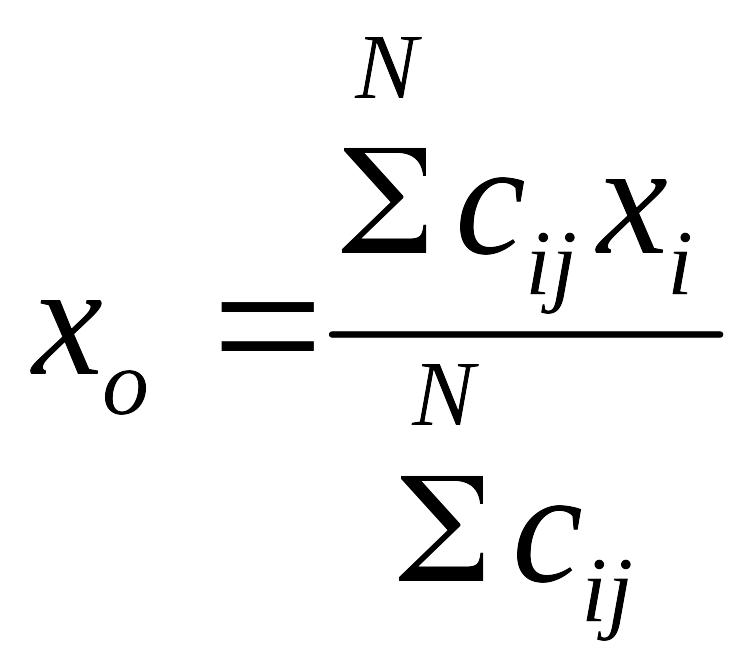В этой формуле N = п² − общее число слагаемых, c_ij − элементы матрицы, обратной к корреляционной.

,

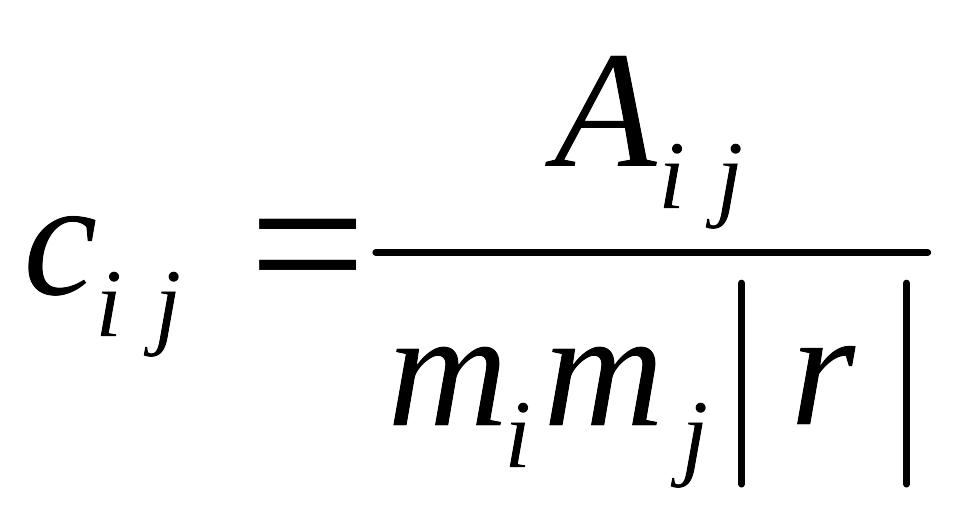где т − СКП навигационного параметра, − определитель, а А_ij − алгебраическое дополнение элементов определителя нормированной корреляционной матрицы

.

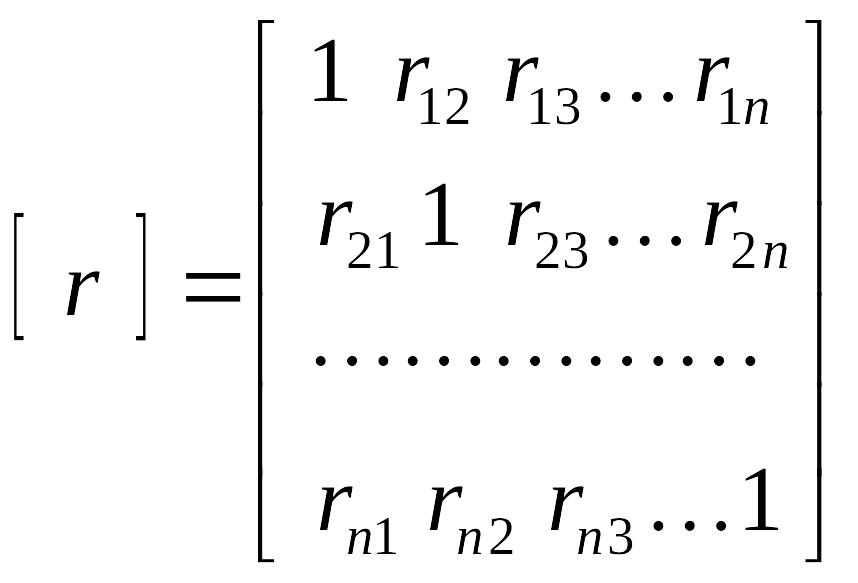Значение А_ij рассчитывается как определитель матрицы с вычеркнутой i строкой и j столбцом.

Перейдем к оценке точности найденного значения навигационного параметра.

Точность навигационного параметра оценивается средней квадратической погрешностью, которая для зависимых неравноточных измерений вычисляется по формуле

,

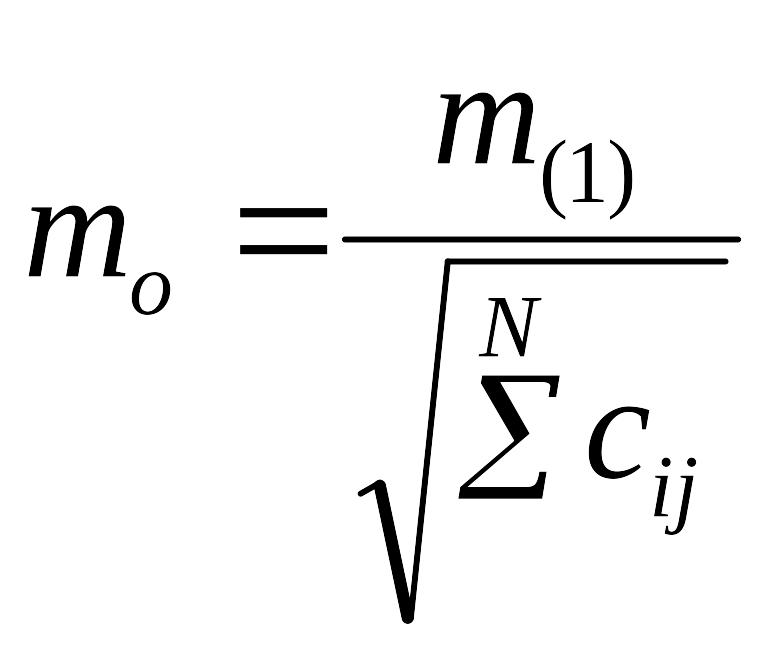где знаменатель вычисляется так же, как и в формуле , а числитель − СКП единицы элемента c_i., Она находится по формуле

.

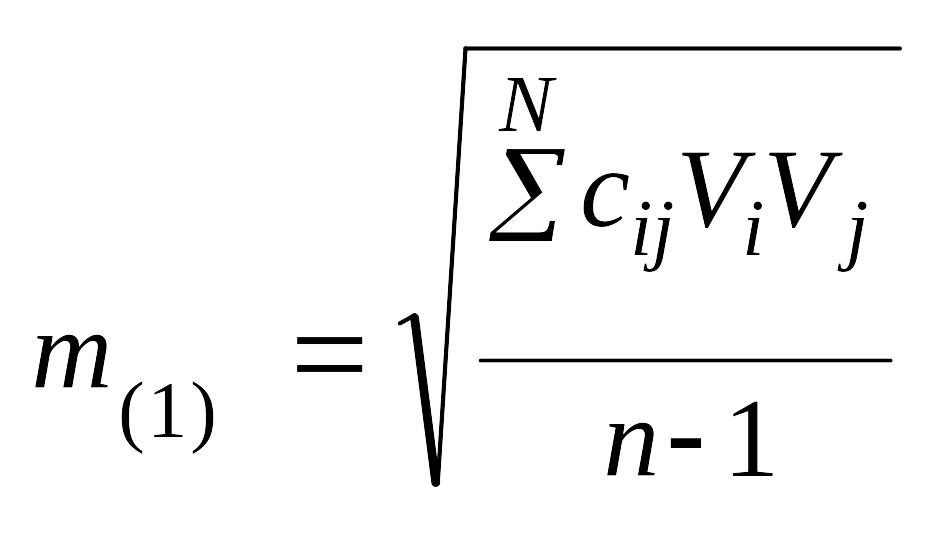При числе измерений меньше 5 формула дает большую погрешность. В этом случае принимают т₍₁₎ = 1 и точность найденного навигационного параметра оценивают по формуле

.

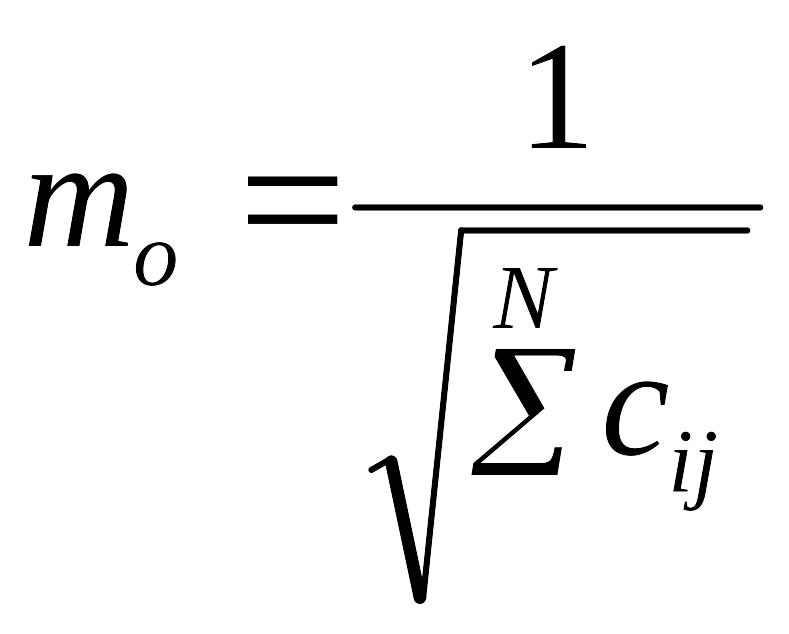Измерения независимые и неравноточные

Если измерения независимы, то коэффициенты корреляции в матрице , кроме диагональных, равны нулю. Тогда все не диагональные элементы А_ij и c_ij также равны нулю. Диагональные элементы А_ij равны 1, а диагональные элементы c_ij равны . С учетом этого формула преобразуется к виду

.

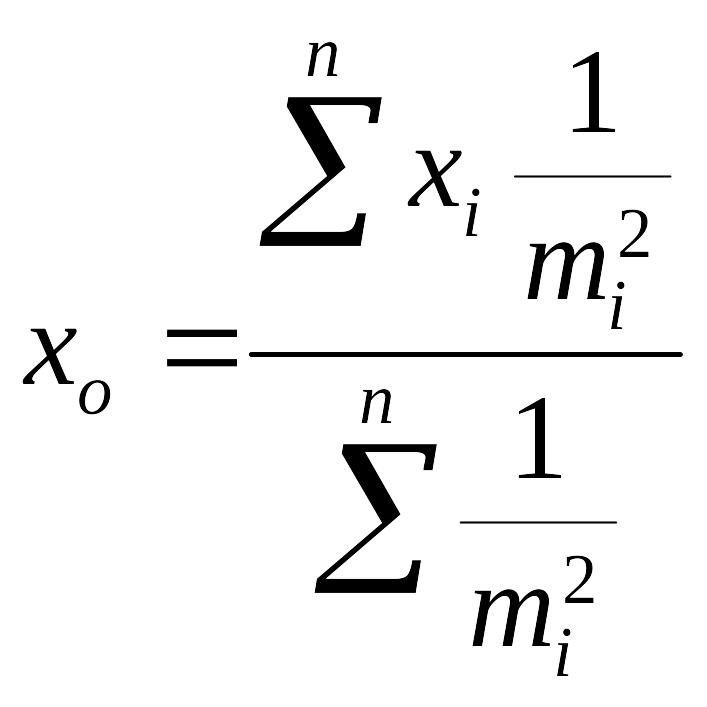Величина

.

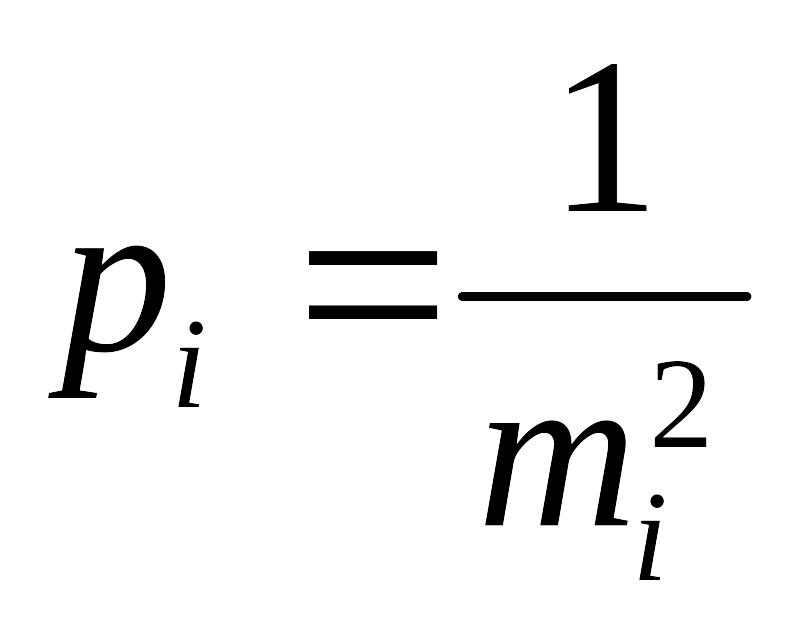называется весом и характеризует степень доверия к измерению. Чем меньше СКП измерения, тем больше его точность и вес.

С учетом формула примет вид

.

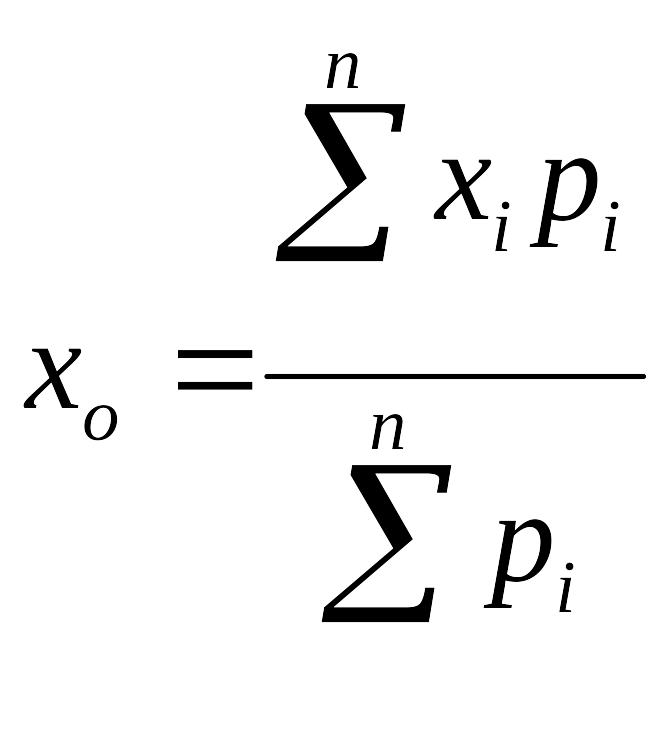Погрешность среднего взвешенного оценивается по формуле

,

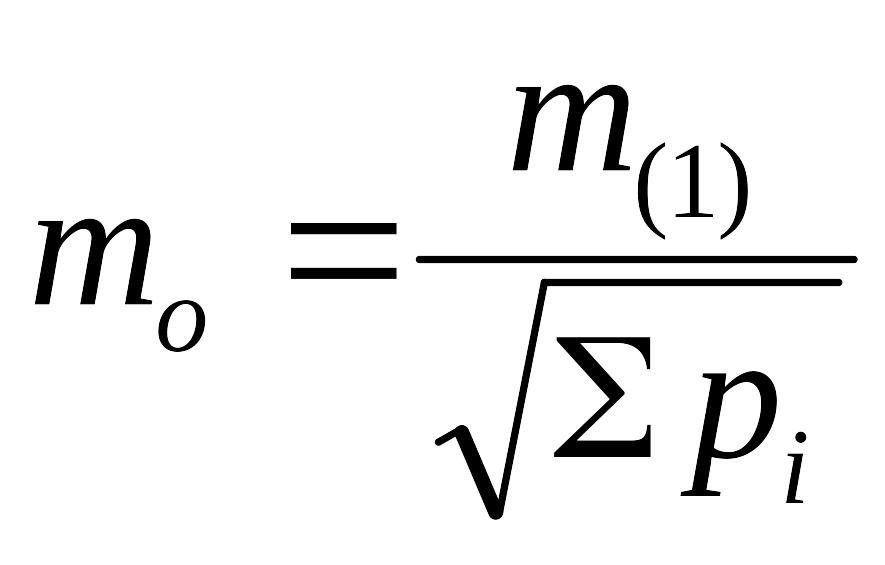где т₍₁₎ − СКП измерения с весом 1, которая рассчитывается по формуле

.

Формулой (6.23) пользоваться при п < 5 не рекомендуется, так как она дает слишком неточный результат. При п < 5 принимают т₍₁₎= 1 и СКП средневзвешенного рассчитывают по формуле

.

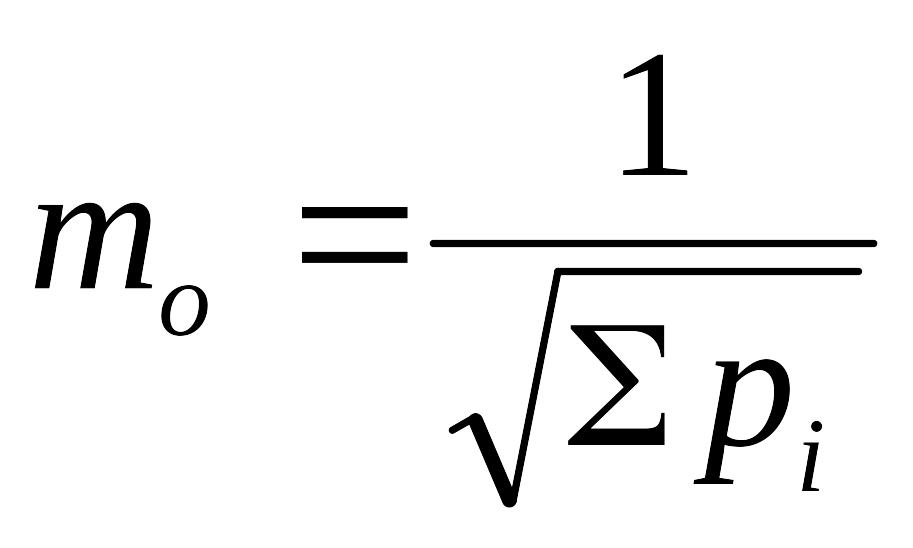Измерения взаимозависимые и равноточные

В этом случае наиболее вероятное значения рассчитывается по формуле

.

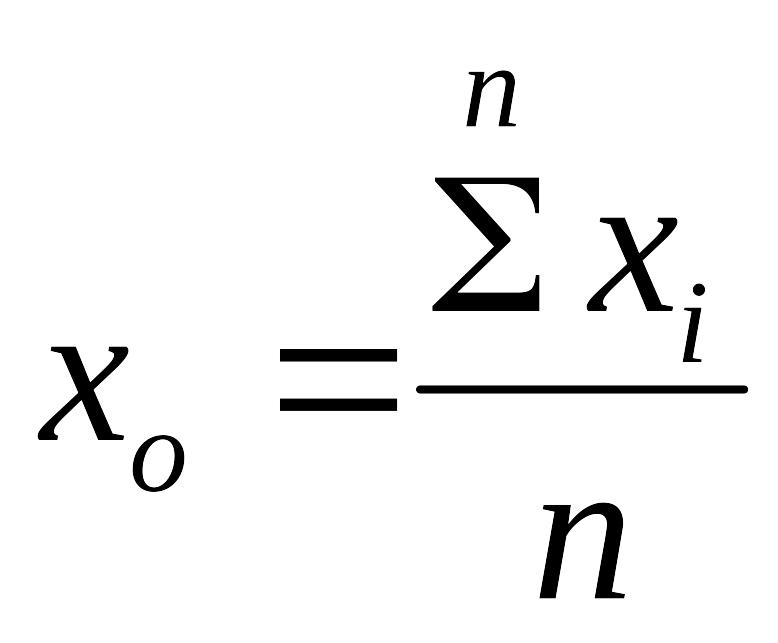Значение, полученное по формуле называется средним арифметическим.

Погрешность среднего арифметического, найденного по зависимым равноточным измерениям оценивается формулой

,

где  - систематическая погрешность,  - случайная погрешность.

Измерения равноточные и независимые

Наиболее вероятное значение навигационного параметра определяется как среднее арифметическое по формуле . Эта формула используется в подавляющем большинстве случаев, потому что измерения, как правило, выполняются одним и тем же наблюдателем, одним и тем же прибором и в одних и тех же условиях. То есть измерения являются равноточными, причем справедлива эта формула и для зависимых, и для независимых измерений.

Погрешность среднего арифметического, рассчитанного по независимым измерениям определяется по формуле

,

где т − СКП измерения параметра.